亲缘选择下不同博弈的收支比b/c对合作进化的影响
岳休云
1 引言
合作者(C)付出代价c,另一个个体获得收益b;背叛者(D)不需要付出任何代价。在进化博弈理论的框架[1]下:一个只包含合作者的种群,由于发生突变出现背叛者,变成了一个合作者和背叛者共存的混合种群,此时合作者相对背叛者繁殖率较低,所以合作者逐渐消失,最后种群完全由背叛者构成(图1)。进化的本质是突变和自然选择,而自然选择青睐背叛,所以自然选择需要相应的机制引导合作。Nowak[2]提出互惠利他主义、亲缘选择和种群选择可以有效地促进合作的进化。

自然选择青睐背叛
亲缘选择机制的本质在于,基因有关的两个体优先考虑与对方发生博弈。Hamilton[3]用r表示亲缘选择的参数(非随机接触的概率),并且得出r>c/b时,亲缘选择引导合作的进化。直接互惠表示:个体间的博弈进行了很多次。个体在每一次博弈时都有两种选择:合作(C)和背叛(D),重复接触的个体有可能会根据对方上一回合的行为来决定下一回合的选择(合作还是背叛)。直接互惠会产生很多策略,如TFT,ALLD,ALLC,WSLS,GTFT等策略。TFT(tit-for-tat)策略者第一次与其他个体博弈时会采取合作行为,如果对手上一次采取合作行为,那么TFT策略者这一次也会选择合作行为,如果对手上一次选择背叛行为,那么TFT策略者这一次也会选择背叛行为,TFT策略会根据对手的行为决定自己的行为。使用ALLD(always-defect)的个体每一次博弈都选择背叛行为。以重复的囚徒困境作为背景,Axelrod[4]研究直接互惠中的随机策略,最终发现TFT策略在引导个体选择合作行为上具有极强的优势。如果TFT策略被ALLD策略侵占并且取代,那么将无法找到任何一个策略可以战胜ALLD策略。所以TFT策略的稳定发展就是合作行为的稳定发展。Ale[5]等考虑亲缘选择与个体间重复接触的概率w建立相应模型,研究结果表明:亲缘选择机制和w的增加有利于合作的进化,但是亲缘选择下不同博弈的收支比b/c对合作进化的影响还不太清楚,下文就这个问题展开分析和讨论。
2 模型与方法
考虑收益矩阵

(1)
其中,C与D分别表示合作和背叛,收益矩阵(1)表示:当C与C相遇时,C获得的收益是a;当C与D相遇时,C获得的收益是b,D获得的收益是c;当D与D相遇时,D获得的收益是d。
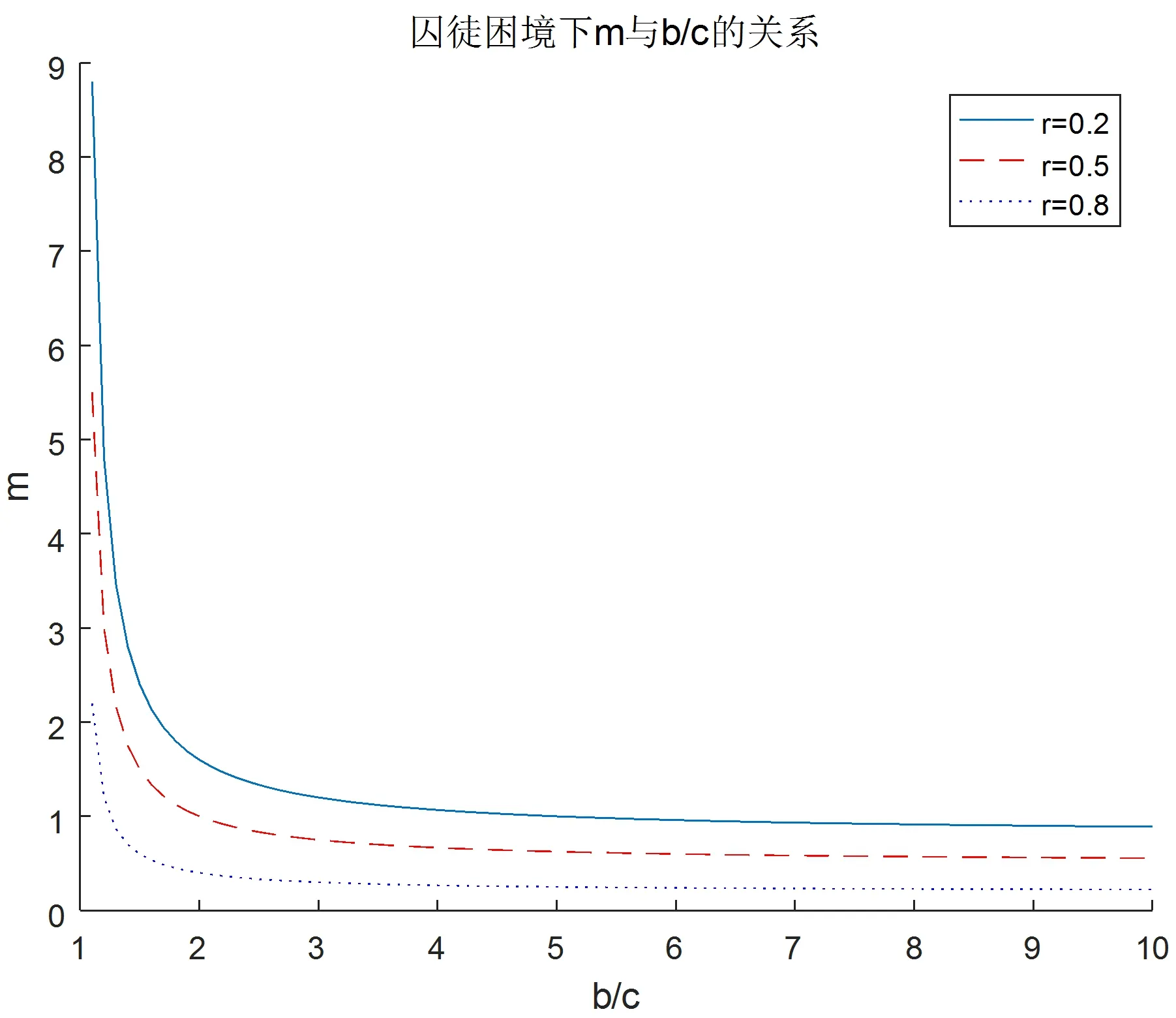
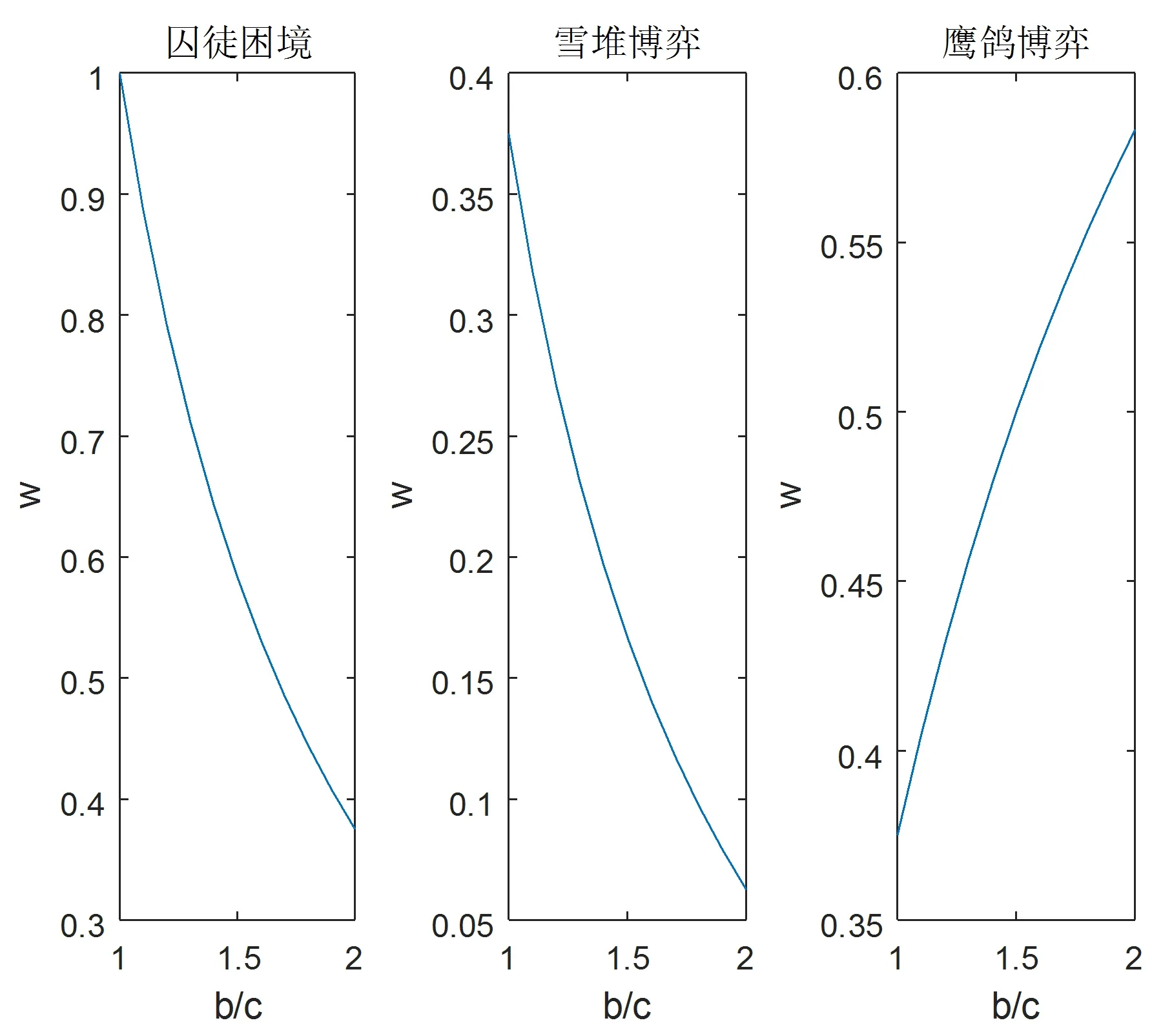
定义r(0 由于亲缘选择下个体之间博弈的收益要兼顾随机接触与非随机接触,所以合作者与合作者博弈的收益要从两方面考虑,首先随机接触下,合作者以1-r的概率随机遇到合作者,此时它的收益是(1-r)a,另外合作者在非随机选择下以r的概率遇到合作者,此时它的收益是ra,兼顾两类接触可见,合作者此时的收益为(1-r)a+ra。同理可得亲缘选择下背叛者与背叛者博弈的收益为(1-r)d+rd。合作者与背叛者博弈,合作者以1-r随机遇到背叛者,此时它的收益是(1-r)b,另外合作者在非随机选择下以r的概率遇到合作者,它的收益是ra,兼顾两类接触,合作者此时的收益为(1-r)b+ra,同理此时背叛者的博弈收益为(1-r)c+rd。基于收益矩阵(1),兼顾两类接触可得 (2) (3) 兼顾个体的两类接触情况,得到亲缘选择下合作者与背叛者进行一次博弈时的收益矩阵为 (4) TFT策略者、ALLD策略者相互之间,自身与自身进行博弈[6]的行为图如(5)所示。 (5) 假设博弈进行的次数为m,忽略个体出错及突变的情况,由(5)式可见TFT策略者与TFT策略者进行博弈时,两个体首次相遇都会选择合作行为,之后由于TFT策略的属性,它们彼此会采取对手上一次的博弈行为,两个TFT策略者往后会一直选择合作行为。由亲缘选择下合作者与背叛者进行一次博弈的收益矩阵(4)可知,两个TFT策略者发生m次博弈获得的收益是ma。ALLD策略者与ALLD策略者进行博弈,由于ALLD策略者的永恒背叛性,两个ALLD策略者会一直选择背叛行为,所以它们各自的收益都为m·d。TFT策略者与ALLD 策略者相互博弈,由TFT策略的属性可知它会在第一次博弈时选择合作行为,往后一直采用对手的行为,所以由亲缘选择下合作者与背叛者进行一次博弈的收益矩阵(4)可知此时TFT策略者的收益为1·[(1-r)b+ra]+(m-1)·d,ALLD策略者一直选择背叛行为,它获得的收益为1·[(1-r)c+rd]+(m-1)·d。个体间的博弈行为发生m次时,亲缘选择下TFT策略者与ALLD策略者的收益矩阵为 (6) 在三种博弈类型[7]-[9]—囚徒困境、雪堆博弈和鹰鸽博弈下建立相关模型,讨论亲缘选择下b/c对合作进化的影响。 囚徒困境: 个体有合作和背叛两种选择,合作者遇到合作者,它们各自的收益都为b-c(b>c)。背叛者遇到背叛者,它们各自的收益都为0。合作者遇到背叛者,合作者的收益为-c,背叛者的收益为b,其收益矩阵如下 (7) 雪堆博弈: 大雪封路导致两名司机同时被困在回家的路上。铲雪表示合作行为,呆在车里休息属于背叛行为,两司机可以选择去铲雪或者待在车里休息。用b表示两司机回家的收益,用-c表示铲雪付出的代价。假如两个司机都去铲雪,那么两人的工作量都将减少一半,这时两人的收益都为b-c/2;假如两司机都在车里休息,只有等到铲雪的机器经过时,雪被机器清理干净后,他们才可以开车回家,这时他们的收益都为0;假如两司机其中一个人去铲雪,而另一个人在车里休息,那么铲雪的司机获益为b-c(b-c>0),休息的司机获益为b。其收益矩阵如下 (8) 鹰鸽博弈: 假设存在两种策略:鹰策略和鸽策略,鹰策略是一种攻击性策略,鹰策略遇到鹰策略会让斗争加剧,之后一个鹰获胜,这过程既有收益又有损失。两个鸽策略者相遇,斗争比较温和,最后一鸽获胜,这过程中只有收益不会有损失。鹰策略者遇到鸽策略者,鹰策略者会让斗争变得更加残酷,此时鸽策略者会选择撤退,最后鹰获得全部收益,鸽由于撤退所以既没有收益也没有损失。假设斗争最后胜者获益为b,败者付出的代价为c。若两者都选择鸽策略(合作),它们不会出现损失,最终其中一个会获胜,其期望收益是b/2,若两者都选择鹰策略(背叛),此时它们成败的概率都是1/2,所以它们最后的期望收益是(b-c)/2,鹰策略遇到鸽策略,由于鸽策略者会选择撤退,鹰策略者不战而胜,此时鹰策略者获益为b,鸽策略者获益为0。将鹰策略看成背叛行为,鸽策略看成合作行为。其收益矩阵为 (9) 由个体之间发生m次博弈时,亲缘选择下TFT策略和ALLD策略的收益矩阵为(6),将囚徒困境,雪堆博弈和鹰鸽博弈的收益矩阵分别代入(6)式可得,个体之间发生博弈的次数为m时,亲缘选择下三种不同博弈类型对应的TFT与ALLD的收益矩阵分别为(10)、(11)、(12)。 (10) (11) (12) 考虑两策略A与B之间的收益矩阵 (13) 一个由A策略者构成的无限大种群,假如有极少的B策略者入侵,A策略者与B策略者的收益矩阵为(13),若a>c,则A策略是进化稳定策略[10](ESS),自然选择会抵制B策略入侵A策略。假设个体间发生m次博弈,亲缘选择下三种博弈类型对应的TFT策略与ALLD策略的收益矩阵(10)、(11)、(12),由进化稳定策略的定义可知 对于囚徒困境下的收益矩阵(10),若满足 m(b-c)>(1-r)b 即满足 (14) 时,TFT策略是ESS。 对于雪堆博弈下的收益矩阵(11),若满足 即满足 (15) 时,TFT策略是ESS。 对于鹰鸽博弈下的收益矩阵(12),若满足 即 (16) TFT策略是ESS。 图2 囚徒困境下,TFT是进化稳定策略的变量关系图 图3 雪堆博弈下,TFT是进化稳定策略的变量关系图 图4 鹰鸽博弈下,TFT是进化稳定策略的变量关系图 在三种不同的博弈类型下,得到亲缘选择机制下TFT是进化稳定策略(ESS)的条件(14)、(15)、(16),由此给出囚徒困境、雪堆博弈和鹰鸽博弈下m与b/c的关系图(图2、3、4)。 由图2、图3及图4可见,亲缘系数r越大,所需博弈次数越少,TFT策略是ESS的条件(14)、(15)、(16)更容易满足,所以亲缘选择机制在这三种博弈类型下都促进合作的进化。由图2、图3可见,m随b/c的增加而减小,但是随着b/c的达到某定值时,变化不再明显,因此在囚徒困境与雪堆博弈的收益矩阵下,b/c在一定范围内逐渐增加促进合作的进化,当b/c达到某定值后对合作的进化没有明显的作用。由图4可见,m随b/c的增加而增加,所需博弈次数越来越多,TFT策略是ESS的条件(16)更加不容易满足,因此在鹰鸽博弈的收益矩阵下,b/c的逐渐减少促进合作的进化。 上面的模型建立在博弈回合数为m的前提下,假设两个体博弈结束,它们之间再次发生博弈的概率是w(0 (17) 基于三种不同博弈收益矩阵下TFT策略是ESS的条件(14)、(15)、(16)中的m此时用1/(1-w)替代,得到囚徒困境下 若满足 (18) 则TFT是ESS。 雪堆博弈下 若 (19) 则TFT是ESS。 鹰鸽博弈下 若 (20) 则TFT是ESS。 考虑各个参数的取值范围,固定亲缘系数r=0.2得出三种博弈收益矩阵下TFT是ESS时b/c与w的关系图如下: 图5 r=0.2不同博弈下b/c与w的关系图 由图5可见,令亲缘参数r=0.2。在囚徒困境与雪堆博弈下,b/c在定区间内逐渐增加有利于合作的进化。在鹰鸽博弈下,b/c在定区间内逐渐减少有利于合作的进化。 将亲缘选择机制引入到不同的博弈类型中,从个体之间发生博弈的次数确定以及不确定两种情况进行讨论,建立相应模型,通过TFT是进化稳定策略(ESS)的条件分析可得:针对三种不同的博弈类型,亲缘选择都有利于合作的进化。 亲缘选择机制下,个体之间发生博弈的次数确定时,囚徒困境和雪堆博弈下b/c在一定范围内逐渐增加有利于合作的进化,当b/c增加到某一定值后对合作的进化并无明显的作用;鹰鸽博弈下b/c的逐渐减少有利于合作的进化。 亲缘选择机制下,个体之间发生博弈的次数不确定时,囚徒困境和雪堆博弈下,b/c在一定范围内逐渐增加促进合作的进化;鹰鸽博弈下b/c在一定范围内逐渐减少促进合作的进化。


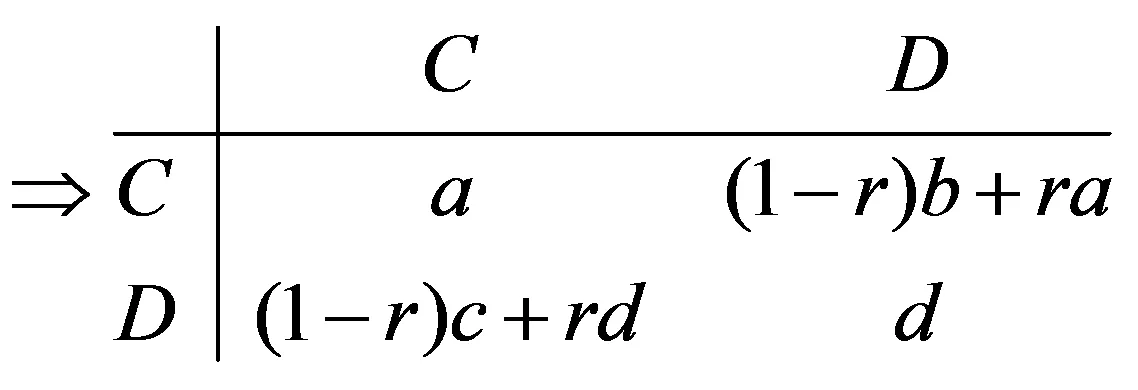


3 亲缘选择下不同博弈的收支比b/c对合作进化的影响
3.1 假设个体间发生博弈的次数为m
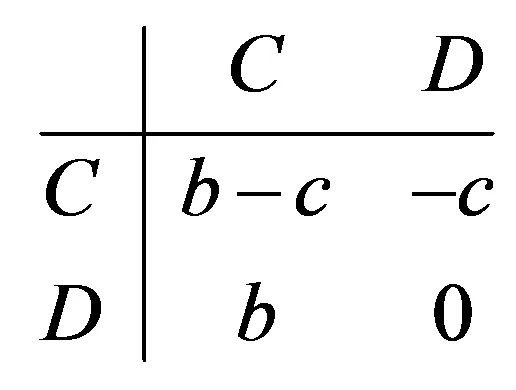
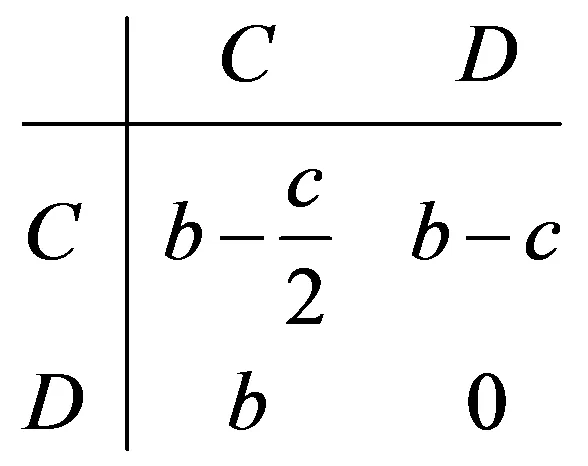
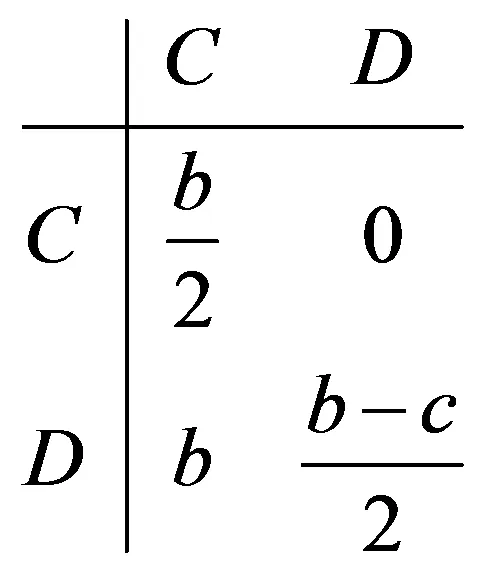






3.2 博弈回合数不确定时

4 结论

