一种新型发动机功率试飞数据处理和代理模型建模方法

周灵玲，邱良军

(中国直升机设计研究所，江西 景德镇 333001)

0 引言

计算直升机的基本飞行性能主要是确定直升机的飞行需用功率和发动机可用功率，当两者相等时就可得到相应状态的基本飞行性能。因此，准确计算发动机可用功率是正确分析直升机基本飞行性能的前提。传统的发动机可用功率处理方法主要采用发动机参数换算和基于百分比的安装损失扣除，无法考虑现代涡轮轴发动机性能曲线的非线性变化，与实测发动机性能曲线特点有所差别。本文提出一种新的发动机功率试飞数据处理方法，并建立发动机可用功率代理模型。通过直升机实际试飞验证，新的发动机功率试飞数据处理方法相比传统的发动机可用功率处理方法，可以考虑发动机性能曲线的非线性变化；运用建立的发动机可用功率代理模型，不仅可以提高发动机功率数据处理和计算的精度，同时还可以考虑发动机安装损失和实际试飞中所需留取的余量。此外，可以使用海平面的发动机试验数据推算发动机安装损失和高原发动机功率，有效提高了高原基本飞行性能的计算精度。

1 传统发动机功率分析方法的弊端

发动机的主要性能参数包括动力涡轮前温度ITT、压气机转速Ng和输出功率Pw，通过给定ITT和Ng阈值限制发动机的工作状态。根据理想循环的发动机模型可以推导得到如下的发动机性能参数换算公式(1)-(3)，其中ITTN为换算动力涡轮前温度，NgN为换算压气机转速，PwN为换算输出功率，θ为温度比，Δ为压力比[1]。

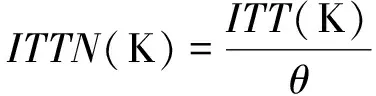
(1)

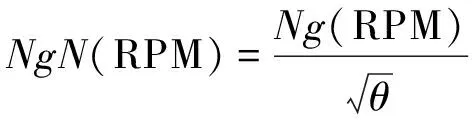
(2)

(3)

传统发动机可用功率处理方法主要通过将不同高度的发动机性能数据点换算后进行数据拟合，获得发动机的性能曲线，再进行反向换算得到所需压力高度和大气温度的发动机性能，然后通过固定的百分比扣除发动机安装损失和功率修正，最终得到发动机可用功率。

对于典型现代民用直升机，平飞状态占其总使用时间超过55%,大部分时间发动机工作在低于最大连续功率的巡航功率状态。以加拿大普惠公司的PT6B发动机(应用于AC313直升机)和法国透博梅卡的Arrius2K2发动机(应用于3吨机)为代表的现代涡轮轴发动机针对这一使用特点，在压气机和燃烧室之间采用放气活门设计，以调节进入发动机后段(包括燃烧室和动力涡轮等)的气流流量，减小压气机能力需求，提高其功重比和经济性[2]。其典型发动机性能曲线如图1所示。在最大连续功率之前的A段，放气活门打开，放走多余气流，保证发动机后段处于效率最高的状态，降低巡航状态的发动机油耗。在最大连续功率之后的B段，放气活门关闭，压气机全力工作以获得更高的起飞功率和应急功率，但是压气机流量仍小于发动机后段所需的最佳流量，燃烧室和涡轮工作效率下降，输出功率随涡轮前温度增长的速度相比A段减小。

图1 某现代涡轴发动机放气活门打开和关闭的

因此，现代涡轮轴发动机的性能曲线通常分为两段，存在两个不同斜率，中间出现拐点，即放气活门关闭点。该放气活门关闭点设计在最大连续功率之前，以提高燃烧室和涡轮效率，降低巡航状态的发动机油耗，并以此点优化压气机设计，减小发动机重量，相比以往根据最大功率设计的老式涡轮轴发动机，可以提高发动机的功重比和经济性。

使用传统换算方法处理此类现代涡轮轴发动机数据，设发动机功率随涡轮前温度ITT增大为线性关系，则可设放气活门打开状态下的发动机输出功率和放气活门关闭状态下的发动机输出功率为下式(4)和(5)。其中，放气活门关闭前后的截距b开≠b闭，斜率k开≠k闭。

Pw开=k开ITT+b开

(4)

Pw闭=k闭ITT+b闭

(5)

根据(1)和(3)式，可推导得换算功率为：

(6)

(7)

则可以得到如下关系式(8)和(9)，表明放气活门关闭前后的发动机性能换算曲线不相等，前述通过换算处理发动机功率的传统方法仅适用于性能曲线线性一致的老式涡轮轴发动机。对于现代涡轮轴发动机，虽然海平面下放气活门关闭前后斜率和截距差别相对较小，但是对比后续第2节的算例，高原条件下的放气活门关闭前斜率比关闭后大30%，截距相差40%，强行使用换算方法处理将引入较大的方法误差。

(8)

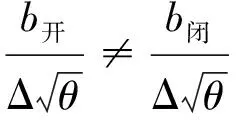
(9)

此外，发动机性能曲线的斜率k和截距b是随压力高度和温度变化的，传统换算方法同样无法考虑由于大气环境导致的发动机换算性能曲线的非线性变化。

因此，理论分析和型号实践都表明使用该方法处理现代涡轮轴发动机数据将带来显著误差，无法满足工程精度要求。

2 发动机性能曲线建模

根据第一节的分析，现代涡轮轴发动机的性能曲线可以抽象成两段相交直线或者二阶多项式的几何模型。根据这个特点可以建立发动机试飞数据的处理方法，并建立发动机功率代理模型，其具体求解流程如下：

1)根据发动机厂商提供的放气活门参考关闭点，对给定压力高度和温度的发动机数据进行分类，区分放气活门关闭前的和关闭后的数据；

2)通过对放气活门关闭点前后的发动机数据分别进行最小二乘法拟合，确定两段直线的截距b闭、b开与斜率k闭、k开，或者二阶多项式系数。设现有n个相同放气活门状态的数据点，对于第i个数据点，其涡轮前温度为ITTi，压气机转速为Ngi，输出功率为Pwi，如使用最小二乘法进行线性回归，可建立数据矩阵AITT与BPw，待求系数矩阵xITT，定义如下：

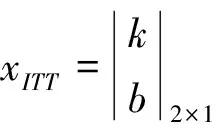
(10)

如使用最小二乘法进行二阶多项式回归，则可建立数据矩阵AITT与BPw，待求系数矩阵xITT，定义如下：

(11)

使用QR分解和最小二乘法求解AITTxITT=BPw，可得涡轮前温度ITT的系数矩阵xITT，确定两段直线的截距b闭、b开与斜率k闭、k开，或者二阶多项式系数。相似方法可算得压气机转速Ng的系数矩阵xNg及其系数；

3)根据发动机厂商提供的发动机功率状态设定ITT和Ng参数限制；

4)由发动机功率状态对应的参数限制求得对应的发动机功率Pw。对于考虑实际飞行操作中给飞行员留予一定的余量的问题，也可以通过直接给定ITT和Ng，求得对应发动机功率Pw；

5)对各个高度和温度组合完成1)到3)的步骤，得到系数矩阵。对于给定的压力高度和温度，通过对数据矩阵进行二维插值得到相应的直线的截距b闭、b开与斜率k闭、k开，或者二阶多项式系数，进而算得发动机功率，从而建立发动机输出功率代理模型。

图2为某现代涡轴发动机高原无地效悬停实测数据算例，可以看出性能曲线拐点前后的曲线斜率和截距有明显差别。使用本文方法可以算得截距b闭=-2890.1和b开=-5059.3，斜率k闭=5.2441和k开=7.9604，对应发动机功率的ITT限制，最大连续功率的PwN为1410kW，最大起飞功率的PwN为1619kW。

图2 某现代涡轴发动机高原无地效悬停实测数据算例

3 发动机安装损失的扣除

传统发动机可用功率处理方法是直接给定各功率状态台架功率，再按固定百分比扣除发动机安装损失后得到发动机的可用功率，如下式所示，其中δ为固定的安装损失百分比，发动机安装损失功率随发动机功率增大而增大。

Pw安装后=Pw台架(1-δ)

(12)

图3为无地效悬停时的典型发动机性能实测数据与台架性能曲线对比，两者之间的差异就是发动机的安装损失。可以看出实测性能曲线与台架性能曲线之间不是固定百分比的关系，而是近似平行偏移的关系，发动机的安装损失功率近似为一个常数，发动机安装损失功率随发动机功率增大而保持不变或者略微减小，与传统按固定百分比扣除的方法的损失变化特性相反。传统方法将高估大功率状态下的安装损失，特别是对于主要对应于大功率状态的基本飞行性能分析，将导致性能损失。此外，传统直接给定各功率状态台架功率的方法也难以根据平行偏移关系计算可用功率。因此，需要使用第2节的方法建立发动机台架性能曲线模型，根据实测数据与发动机基准性能曲线对比获得性能曲线平行偏移量，对发动机台架性能曲线模型进行平行偏移后得到扣除安装损失后的发动机性能曲线。设发动机台架功率为ITT的函数，记为Pw台架(ITT)，则扣除发动机安装损失后得到发动机的可用功率函数Pw安装后为：

Pw安装后(ITT)=Pw台架(ITT-ITT偏移量)

(13)

其中ITT偏移量为相同输出功率下，台架性能曲线的对应ITT与实测性能曲线对应ITT之差。

图4为发动机在不同压力高度无地效悬停实测性能曲线ITT偏移量对比。

由图4可以看出海平面的平行偏移量和高原的平行偏移量大致相当。在只有海平面试验数据时，可以使用海平面的发动机试验数据推算ITTN平均偏移量，进而获得高原发动机可用功率，有效提高高原基本飞行性能的计算精度。在获得高原试飞数据后，可以对ITTN偏移量进行线性拟合，从而进一步考虑发动机安装损失随压力高度的变化。

图3 某现代涡轴发动机无地效悬停实测性能曲线和台架性能曲线对比

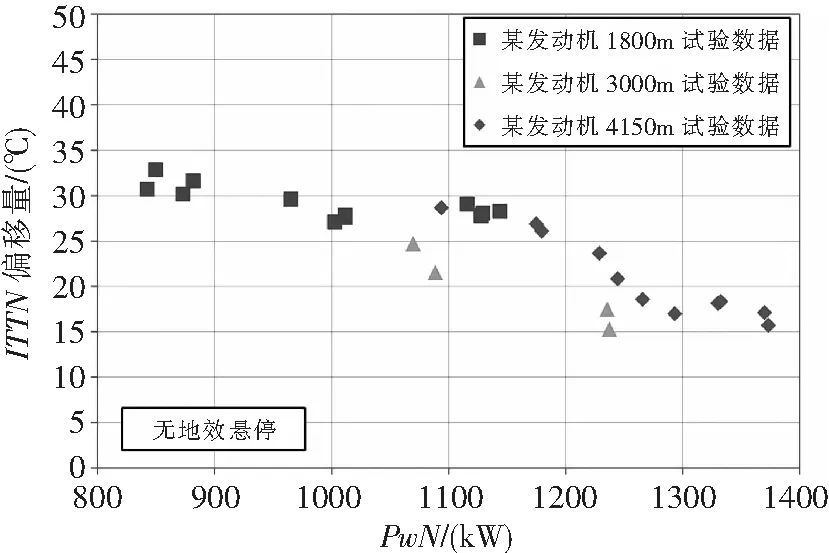
图4 某现代涡轴发动机不同压力高度无地效悬停实测性能ITT偏移量对比

4 计算结果与实测性能对比

图5为新的发动机功率处理结果、传统换算方法处理结果以及实测数据对比图。

图5 新的发动机功率模型起飞功率计算结果和传统换算方法计算结果对比图

可以看出，传统方法在低高度的计算结果，发动机功率随高度减小反而减小，计算结果不合理。新的发动机可用功率处理方法相比传统方法能够更准确地描述发动机可用功率随压力高度的变化，处理结果更加准确有效。

5 结论

本文提出一种新的发动机功率试飞数据处理方法，并建立发动机可用功率代理模型。型号验证表明，该方法相比传统分析方法主要有如下优点：

1)可以考虑发动机性能曲线的非线性变化，显著提高发动机可用功率计算精度，计算结果的性能曲线趋势合理；

2)发动机安装损失处理方法与实测损失特性相符，可以使用海平面的发动机试验数据推算安装损失和高原发动机可用功率，有效提高高原试飞数据处理精度和高原基本飞行性能的计算精度；

3)可以更简便地考虑实际试飞中所需留取的余量，方便试飞任务仿真计算。