斐波那契数列与走楼梯

浙江省杭州市天长小学 数学实验组/供稿

向你介绍我是谁

萌萌一枝花，才学素养品德佳，圆脸蛋，爱微笑，这就是我，天长小学二（2）中队的王韵菲。不要以为我只会卖萌，其实我还有许多特长爱好!我喜欢数学、阅读、科学等。我的梦想是成为一名牙医，让大家胃口好、身体棒！

研究起点：

平时走路或上楼梯时，妈妈总是要在身后叮嘱我一步一步好好走，但其实“不走寻常路”也可以研究数学哦！你可能没发现，“走楼梯”里蕴含着有序思考的数学思想，对我们今后解决问题会有很大的帮助。

研究问题：

假设一楼到二楼的楼梯有6级台阶，若1步只能走1级或2级台阶，请问到二楼有多少种走法？

研究过程：

让我们通过画图的形式，演算不同走楼梯的方法各需要几步才能走到二楼吧！

1.

全部走1级：1+1+1+1+1+1=6，一共需要6步。这样只有1种走法。

2.

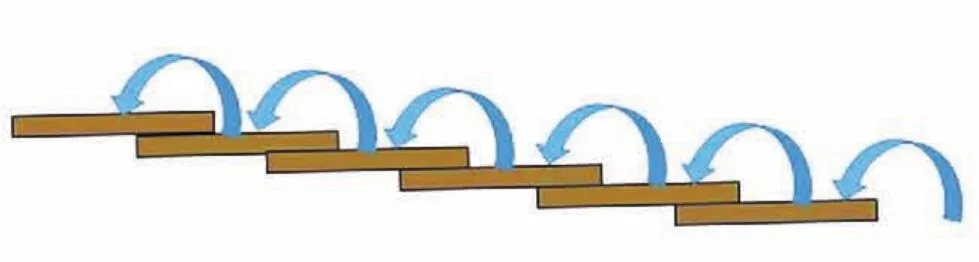
只走一次2级，其余都是1级：2+1+1+1+1=6 ，一共需要5步。我们只需要考虑哪两级台阶用1步走完就可以了。这样有5种走法。

3.

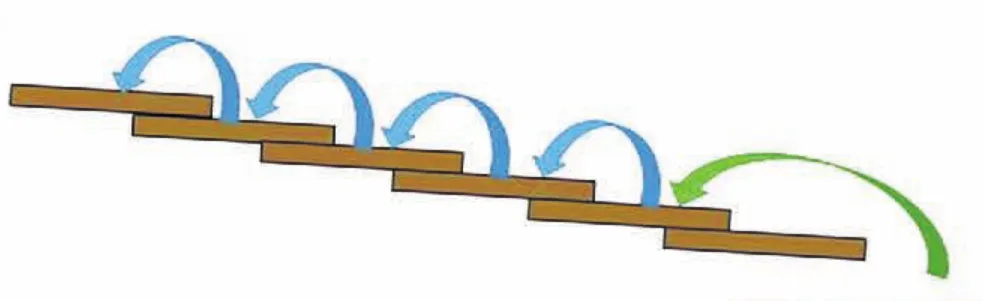
只走二次2级，其余都是1级：2+2+1+1=6，一共要走4步。我们只要思考这4步的顺序如何安排。如果我们给这4步编号（1、2、3、4），并在其中选择两步来跨2级台阶。那么选择的方法有：1和2、1和3、1和4、2和3、2和4、3和4，共有6种。

4.

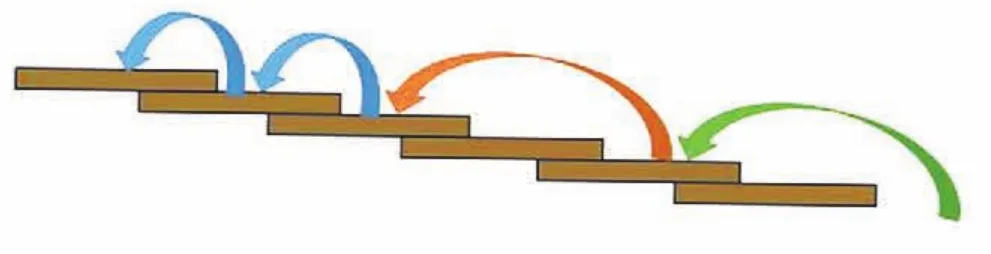
全部走二级：2+2+2=6，全部走两级只要3步，而且只有1种走法。

研究结论：

如果每一步只能走1级或2级，6级台阶一共有13种走法。

深度思考

算清了这些之后，我又有了新的思考：如果不是6级台阶，那有没有什么办法马上知道一共有几种走法呢？我从一级台阶开始思考，发现其中确实有规律。

一级台阶，1种走法；

二级台阶，2种走法；

三级台阶，3种走法；

四级台阶，5种走法；

五级台阶，8种走法；

六级台阶，13种走法；

七级台阶，21种走法；

八级台阶，34种走法……

你们发现了吗？1,2,3,5,8,13,21,34……哇哦，这可是著名的斐波那契数列，又称兔子数列。这个数列的规律就是前两个数的和等于第三个数，它一开始是被用来计算这样一个问题：假定一对刚出生的小兔一个月能长成大兔，再过一个月便能生下一对小兔（公母各一），并且此后每个月都生一对小兔。如果没有兔子死亡，那么兔子的数量就会按照这个数列逐渐增加。你发现这个规律了吗？