一种失真或旋转QR码的定位算法

赵健雄 费树岷

摘要：为了解决传统算法QR码定位中出现QR码失真，或旋转时出现较弱鲁棒性的现象，提出一种新型QR码自适应定位算法。在算法研究过程中，首先使用自适应阈值算法解决不均匀照明的影响，在此基础上提出一种基于轮廓跟踪与轮廓筛选的定位方法。实验结果表明，与传统QR码定位算法相比，该算法定位准确率提高了30%，且定位速度提升了17%，可见该定位算法能够很好地应用于QR码定位。

关键词：QR码本地化;轮廓跟踪;回转;失真

DOI：10.11907/rjdk.182922开放科学（资源服务）标识码（OSID）：中图分类号：TP312文献标识码：A 文章编号：1672-7800（2019）010-0086-04

0引言

与1D条形码相比，2D条形码在两个方向上记录数据。由于其具有高数据压缩性及高可靠性的特点，以及较强的纠错能力，被广泛应用于许多领域。QR码代表快速响应代码，由Denso于1994年提出，之后被广泛用于编码超链接或加密识别。

如图1所示，QR码是由黑白方块组成的矩阵，称为模块。每个QR码具有3个用于检测位置与旋转的取景器图案（FIP）。另外，每个OR码包含两个定时模式（TP）、一定数量的对准模式（AP）和数据区域。详细信息可参阅2000年12月28日发布的QR码国家标准。

旨在快速、准确识别QR码的设计算法已成为当前的研究热点。大多数识别算法利用QR码形态特征，如文献[7]中提出的定位方法。利用FIP中黑白像素比例1：1：3：1：1的原理，可以通过霍夫变换得到条形码边界线与顶点位置，该算法很常见且较为成熟，但也存在一些缺陷。当QR码旋转45°或失真时，文献[9]提出的算法无法很好地工作，而文献[10]提出的算法对嵌入式系统而言，计算复杂度太高。同时，当图像中QR码比例较小时，文献[11]中算法效果不佳。因此，本文提出一种基于轮廓跟踪与轮廓筛选的失真或旋转QR码定位方法。

1QR码本地化

本地化是QR码识别的关键步骤，准确性是本地化的重要评价指标。本文提出方法基于轮廓跟踪和轮廓筛选获得FIP轮廓，并在定位之前，通过文献[12]提出的自适应阈值算法对图像进行预处理以获得二值图像。

1.1轮廓跟踪

在本文中轮廓是指对象的封闭轮廓。关于轮廓跟踪有多种算法，例如OpenCV中的cvFindContours函數，但其对于嵌入式系统而言过于复杂。本文提出的算法基于。cv-FindContours函数与Suzuki提出的轮廓跟踪算法，但对QR码进行了改进。该方法具有低时间与空间复杂性。

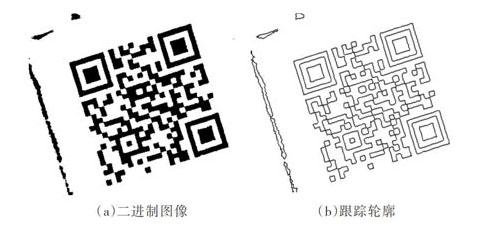
扫描后找到轮廓，图2（a）是输入图像，图2（b）表示算法1跟踪的轮廓。

输入：已经过预处理的二进制图像。设输入图像为F={f_ij}，f_ij表示位于（x，y）的像素值。算法简要步骤如下：

输出：图像中的所有轮廓。

（1）初始化：将图像的最外围像素设为0，并将最初的NBD设为1。

（2）用电视光栅扫描图像，如果f_ij-1=0且f_ij=1，则确定像素（i，j）是轮廓起点，转到步骤（3）。

（3）从起点（i，j）增加NBD，（i_o，j_o）←（i，j），（i₂，j₂）←（i，j-1），跟踪检测到的轮廓，可通过以下子步骤完成：①从（i₂，j₂）开始，顺时针观察（i，j）附近像素并找到非零像素。设（i₁，j₁）是第一个找到的非零像素，如果未找到非零像素，则转到步骤（2）;②（i₂，j₂）←（i₂₁，j₁）←（i₃，j₃）←（i₀，j₀），f_i3，j3=NBD。保存（i₃，j₃）作为轮廓的一个点;③从逆时针顺序像素的下一个元素（i₂，j₂）开始，检查（i₃，j₃）附近像素，将第一个非零像素点置为（i₄，j₄）;④f_i3，j3=NBD，并将（i₃，j₃）保存为轮廓点;⑤如果（i₄，j₄）=（i₀，j₀）和（i₃，j₃）=（i₁，j₁）（回到起点），则回到步骤（2），否则，（i₂，j₂）←（i₃，j₃），（i₃，j₃）←（i₄，j₄），转到步骤③。

1.2轮廓筛选

QR码轮廓筛选是一个特殊过程。经过大量的重复测试与分析，本文提出一种新型算法，该算法由一些基于QR码中FIPs图形特征的有序滤波器准则组成。

在跟踪轮廓之后，获得包括背景和QR码的所有轮廓。每个轮廓表示为C_i，j是轮廓序列号。每个轮廓长度表示为T_i，并且所有点表示为p_ij。根据获得的信息，可通过计算获得更多信息，该信息有助于获取FIP和QR码的位置。每个轮廓都有自己的最小水平包围矩形。遍历轮廓C_i的所有点P_ij（j∈1，2…T_i）以获得单坐标轴中的最大和最小像素，并保存为：真x_max、x_min、y_max、y_min通过以下方法计算每个轮廓最小水平包围矩形的长宽比：R=X_max-X_min/y_max-y_min。在无噪声和失真的理想情况下，FIP轮廓长宽比为1。

FIP的最小轮廓是3*3模块的轮廓。因此，FIPs轮廓长度应满足一定要求（T_i>T）。即使保留短轮廓，也难以在后续步骤中进行识别。

FIP的轮廓是3个正方形，理想情况下其中心相同。计算轮廓C_i的中心M_i，如果轮廓中心与其它两个轮廓重叠，则将该轮廓标记为FIP的轮廓。

实际上，由于环境、图像分辨率、旋转和透视畸变的影响，FIP轮廓参数可能不能完全符合上述标准。因此，相关标准应该允许一些容差，以适应由于各种条件导致的不精确性。

定义1（比率标准）：当且仅当1-Ei<1+E时，轮廓的最小水平包围矩形长宽比满足长度标准。

例如，E=0.2意味着最大允许比率差异为20%。

定义2（长度标准）：轮廓满足长度标准，T_i>T，其中T_i表示闭合轮廓中的像素数。

定义3（重叠标准）：轮廓满足重叠标准。

Dist（M_i-M_j）i-M_k）

设M_i、M_j为两个轮廓的中心像素，Dist（M_i-M_j）表示两点距离，参数d应允许小的变化。

在算法2中，F_i是轮廓C_i的标志，如果轮廓不满足标准，则F_i将被设置为-1。第1-3行对应初始化，F_i初始化为0，第4-11行对应于比率与长度标准，如果轮廓不满足相应公差标准，则将标志设置为-1。第12-18行的遍历是算法主要部分，其中轮廓被筛选之前将检查轮廓中心是否重叠，筛选的轮廓将被添加到输出列表中。

具体轮廓筛选算法如下：

1.循环遍历C_i

2.创建一个标志F_i并将其初始化为0

3.结束

4.循环遍历C_i

5.如果R_i不滿足比率标准和公差E

6.将-1分配给F_i

7.结束

8.如果T_i不满足长度标准，则

9.将-1分配给F_i.

10.结束

11.结束

12.循环遍历C_i

13.如果F_i≠-1

14.如果真M_i满足重叠标准，则

15.将1分配给F_i，并将C_i添加到输小列表

16.结束

17.结束

18.结束

图3（a）-图3（c）显示了算法2中不同滤波器标准的轮廓。在分析与计算FIP轮廓信息后，将获得顶点位置、版本及其它信息以帮助识别。

经过大量640*480图像的测试与分析后，将参数设置为E=0.2，d=3，以获得最低失败率（误识别或无法识别）。

2 QR码本地化表现

为了评估本文提出方法的鲁棒性和准确性，从分辨率、旋转角度和畸变角度比较与分析不同测试集效果。

2.1图像分辨率变化

测试装置1-3的图像分辨率分别为320*240、640*480和960*1280，每组有60个图像，并且每个图像包含版本1-6中的完整QR码。

相对误差E=（|AoA|+|BoB|+|C_oC|）/3，其中A、B、C是本文方法得到FIPs附近OR码的3个顶点，A_o＼B_o、C_o是手动获得的顶点，|AoA|表示两点距离。设E表示每组相对误差平均值。

图4显示了不同图像分辨率下的检测率与检测误差平均值，可以看出检测率很高，且误差率较低。

2.2旋转与失真角度变化

图5、图6为对复杂背景中QR码旋转或失真时的性能分析，因为QR码的条件在实践中是变化的，稳健性对于定位方法非常重要。图5表明QR码旋转角度很少影响定位效果，旋转角度范围为0°-150°，步长为30°，还分析了透视畸变对定位的影响，透视畸变范围为0°-35°，步长为5°。图6显示了不同QR码失真角度对定位性能产生的不同影响。当失真小于20°时，该方法效果很好，但当角度为35°时，因失真太严重而导致无法检测。

2.3QR码本地化案例

当QR码旋转角度约为45°时，文献[14]中提出的方法将无法发挥作用，因为在水平和垂直扫描中，比率满足1：1：3：1：1的情况很少。本文提出方法在理论上不受旋转影响，旋转或扭曲的QR码示例如图7所示，图中红线为FIP轮廓。

通过霍夫变换检测边界线和顶点位置将受到背景干扰。图7中的QR码即使在严重扭曲、旋转或具有复杂背景的情况下，都可通过本文提出的算法进行定位，

3结语

当QR码出现旋转、失真或背景复杂情况时，提高图像定位性能具有重要意义，以便更好地进行QR码识别。本文提出的定位算法具有对复杂背景、旋转和失真的鲁棒性。通过自适应阈值算法获得二值图像的定位预处理方法结合了全局阈值和局部阈值的最佳值。定位算法基于QR码中FIP_s的几何特征，通过轮廓跟踪与轮廓筛选得到准确位置。测试结果表明，当QR码随机旋转并在20°角度内扭曲时，该方法是健壮且精确的，但当QR码严重扭曲时，定位可能是倾斜的，需要对图片进行预处理，可以在检测之前使用图像去噪方法或超分辨率方法恢复劣化图像。