基于ABAQUS驱动钢结构断裂损伤探究
王 铎,沈振辉,蒋国平,杨拴强
(福建江夏学院工程学院,福州350108)
0 引言
钢材(Steel products)多用于钢材混凝土和预应力钢材混凝土,在土木工程中的应用非常广泛。分析构件结构的内力与应力时,通常运用线弹性理论计算。抗拉强度是衡量钢材抵抗塑性损坏的重要标准,钢材承受外载荷的极限指标由抗拉强度确定,其能够显示出钢材达到屈服极限后尚有多少强度储备。这种方法确定钢材极限承载能力时通常采用大量拉伸实验数据确定截面破坏时的应力分布情况和经验计算公式[1]。采用实验方法对于常规设计较为合适,并且通常适用于梁、板等简单构件。当需要考虑结构中材料的非线性因素,如结构损伤、结构塑性、结构断裂等现象时,就缺少相应的计算公式[2]。
随着计算机计算能力的迅速发展,有限元分析在机械、土木、材料、铁道工程、航空航天、船舶、电器、机加成型等各个工程领域得到广泛应用[3-4]。在解决非线性问题的有限元模拟软件中,ABAQUS表现最为突出,是高校和企业通用的大型分析软件,它始终专注于汲取最先进的分析标准和计算机技术,引领着全球非线性有限元分析技术的成长。ABAQUS软件已被全球工业界广泛接受,并拥有大量的非线性力学用户群[4]。
1 ABAQUS损伤塑性模型理论
金属材料单轴拉伸应力—应变曲线存在四个阶段。应力超过极限强度值以后卸载时存在残留塑性应变现象,这与金属材料内部存在微小裂缝(损伤)有关。探究材料存在缺陷时,通常采用损伤力学和断裂力学这两种手段。对金属构件采用拉伸变形时,其内部形成众多细小滑移和损伤裂痕,简单地简化为几条裂痕而采用断裂力学方法研究是不可取的。对于钢材这类金属构件,其受到外力时内部产生细小裂痕和细微空腔,损伤力学适宜研究金属构件受外力时产生损伤的发展和演变。ABAQUS软件包括大量的分析模块,损伤塑性模块是其中一种。该模块在金属构件分析中引入损伤指标,有效地模仿钢材拉伸引发强度因损伤增加而降低的特点,适用于钢材结构的非线性分析。
ABAQUS提供的钢结构损伤塑性模型是依据Kachanov[5],Raboinov[6],Lemaitre[7]等人提出的损伤塑性理论确定的,采用设定连续性参变量的方法,分析构件中损伤演化[8]的复杂进程,参变量即为损伤变量,由此建立损伤模型的本构方程。
在金属构件模型中加入ABAQUS损伤塑性模块中的损伤指标,建立损伤演化的本构模型,检验损伤模型的有效性、合理性,并把计算出的最终结论同试验结论进行对比。
2 延性金属损伤塑性模型理论
过度变形和不可逆的变形都会导致金属发生延性破坏。在金属构件中,微缺陷或滑移出现在过度变形较大的位置,变形过程中大规模扩展,表现为形成损伤。对金属材料而言,何时发生损伤是重要的因素。
2.1 延性金属塑性分析
材料在外载荷作用下发生不可逆的、永久性的形变,称为塑性形变,其是材料本身的一种属性。对绝大多数线弹性的工程构件施加外载荷,当产生的应力小于比例极限时,应力-应变曲线表现为线性关系;当应力超过比例极限或屈服点后,材料会发生屈服特性,此时材料的响应变成非线性和不可逆。
金属构件的工程应力也称作名义应力[9],即F/A0,同名义应力相对的物理量称作名义应变,即△l/l0。在单向拉伸与压缩试验中得到的数据通常都是以名义应力和名义应变给定的[10]。
当设定△l→dl→0的情况下,拉伸与压缩的应变表示方式是一致的,即
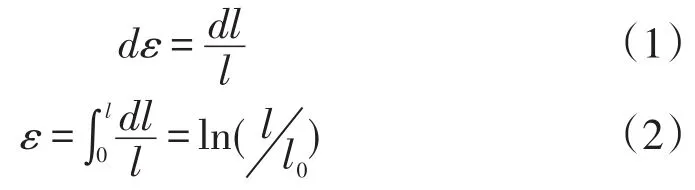
式中,l0是初始长度,l是当前长度,ε是真实应变。
与真实应变对应的真实应力为

其中,F为构件上所受的力,A为构件当前横截面面积。
在ABAQUS显示分析模块中,材料的塑性指标必须选取真实应力与真实应变进行表征,必须采用公式将塑性材料的名义应力、应变转换成真实值。
因为构件塑性形变存在不可压缩的特性,所以将真实长度、面积同名义长度、面积的关系表示如下:

当前面积与原始面积的关系:

将A的表达式代入真实应力(3)式中,得到
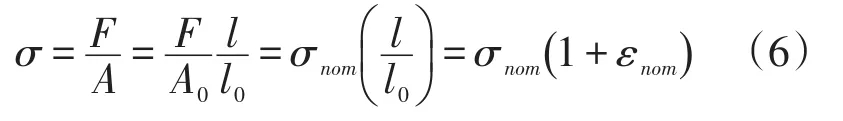
真实应力值与名义应力值的关系表达式为

名义应变为
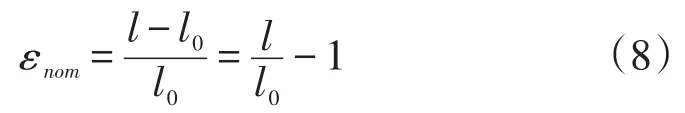
将(8)式等号左右两边分别加上数字1,而后对等号两边分别取以e为底的自然对数,解得名义应变与真实应变两者的关系表达式如下:

在ABAQUS材料非线性分析中,塑性应变与弹性应变相加组成总体应变。所以,要想得到塑性应变,只需在总体应变中减掉弹性应变即可。真实应力与弹性模量E的比值,得到弹性应变,表达式如下所示:

式中,εpl是真实塑性应变;εt是总体真实应变;εel是真实弹性应变。
2.2 损伤演化
材料在达到屈服点之前,表现为弹性;当超过屈服点后,材料表现为幂硬化。一维物理关系为
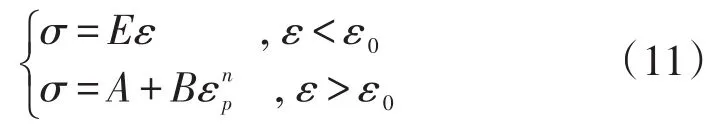
式中,A、B、n为材料常数,通过实验获得。
进入屈服阶段后,材料的变形和损伤均为单向不可逆的过程。当发生损伤时

式中,˙取正值,表明损伤的不可逆性。金属三轴比是影响断裂的另一重要特征,可以采用三轴因子RV表征,它包含在Y表达式中。
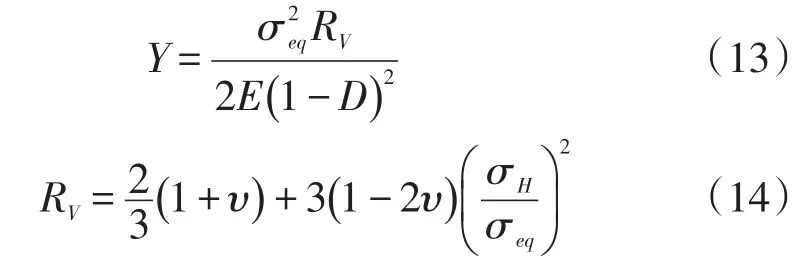
将关系式(13)和(14)分别代入(12)式后,损伤模型的本构方程解得
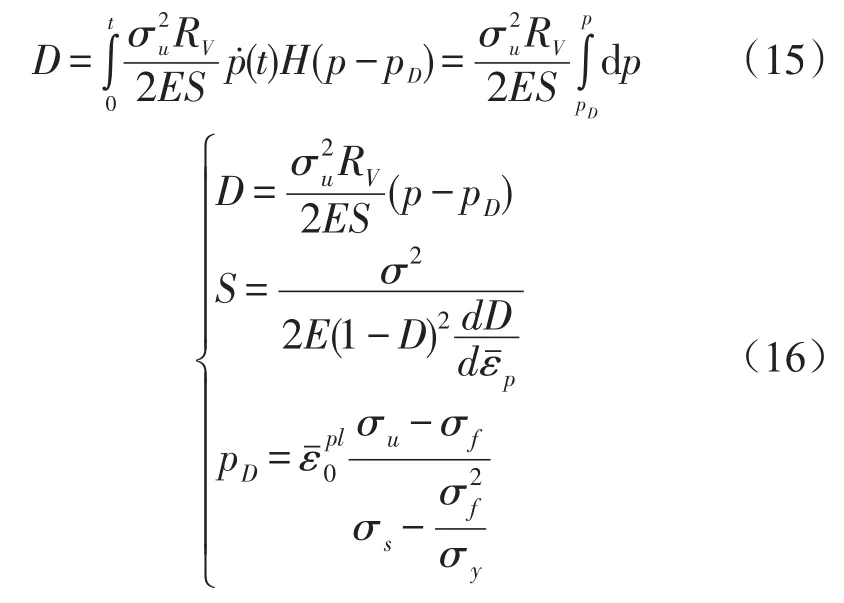
本例中采用低碳钢材料,考虑到材料的各项同性强化法则、幂次强化模型、应变等效理论和屈服准则等因素,由(11)、(15)和(16)式,得
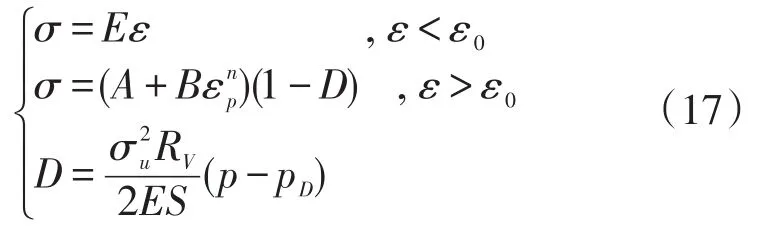
3 低碳钢单轴拉伸试验
3.1 单轴拉伸弹性阶段
本例在福建江夏学院力学实验室进行,采用标准单向拉伸试件,低碳钢Q235。弹性模量E=2.55×105MPa,泊松比ν=0.3,强度极限101MPa,最大拉力10.1185kN,应力、应变取3106对坐标点。
材料图片如图1所示。

图1 低碳钢管拉伸试件
根据ABAQUS分析流程规定,承受拉伸外载荷作用的构件会产生拉伸应力状态,其损伤演化率要采用数据列表的方式录入,如表1所示。
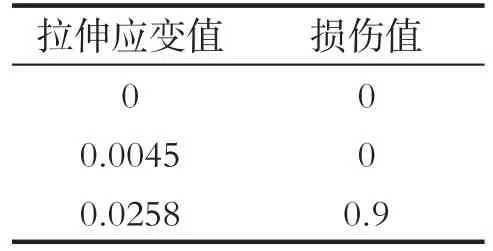
表1 拉伸应变值与损伤值的对应关系
验证拉伸模型在上述材料参数下的力学性能。本模型采用与实体构件同尺寸设计。
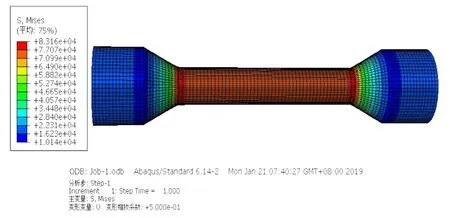
图2 单向拉伸试件弹性拉伸应力分布图
ABAQUS分析结果如图3所示,在线弹性阶段,应力-时间和位移-时间曲线均符合低碳钢弹性阶段图像相形态。

图3 应力、位移-时间曲线
3.2 低碳钢拉伸损伤有限元分析
进一步检验低碳钢模型拉伸破坏下的力学特性,根据实验特点设定相应的损伤因子。单元数761个,单元类型CAX4R,模型下端固定,右端向右受到拉伸位移作用,拉伸位移值8mm(方向与Y轴一致)。
实验表明,颈缩阶段出现之前,试样标距范围内的伸长沿试样长度均匀分布。颈缩现象出现之后,试样变形主要集中在颈缩区域,如图4所示。低碳钢试样拉伸断裂以后,在断面处呈现出韧性杯锥形状的断口,在断口处构件直径明显缩小,即产生颈缩。这与实际拉伸实验中构件断口处的形貌一致。断口处产生应力极值,如图5所示。分析低碳钢材料拉伸的力学性能时,在实验中拉伸变形曲线具有典型性,呈现明显的四个部分,分析实验结果大致如下:1)弹性阶段,应力与应变满足胡克定律,成正比关系;2)屈服阶段,应变变化量继续增加,而应力变化量不大且出现上下小范围波动现象;3)强化阶段,构件的抵抗能力重新恢复,要想产生应变,必须增加应力;4)局部变形阶段(又称颈缩阶段),构件的某一局部径向尺寸明显急剧缩小,产生颈缩。从图6中可以清楚看到上述四个阶段。应当指出,由于试验描绘出的伸长△L是整个试样的伸长,而不只是标距部分的伸长,其中还包括试验机本身的弹性变形和试样头部在夹板中的滑动等[11]。单轴拉伸试验刚进行时,棒材头部与夹板接触面存在相对位移,导致试验初期滑动较大。随着实验的进行相对位移消失后,不再出现滑动。所以绘制出来的拉伸图像中,在最初一段呈现曲线状态,因此应由弹性直线段的延长线与伸长轴的交点作为拉伸图像的坐标原点O,过O点作力轴F,如图6所示。在低碳钢拉伸等比例阶段,试件不发生损伤,当拉伸时间到达19.85s时,进入到屈服阶段,该阶段试件表面产生滑移线,表明损伤已经形成并且不断延续。随着损伤的不断扩大,损伤随时间不断增长,呈现线性关系,如图7所示。

图4 单轴拉伸试件整体等效塑性应变分布图

图5 单轴拉伸试件局部等效塑性应变分布图

图6 应力-应变全过程曲线

图7 损伤-时间曲线
4 结论
1)本文依据材料的单轴受力应力-应变非线性理论、塑性形变原理和损伤力学原理,推演出延性金属的弹塑性损伤模型。通过ABAQUS/Standard显示分析,研究在损伤的情况下构件各项力学指标的响应规律。
2)采用钢构件受单向拉伸集中力载荷作用,在弹性阶段材料变形可以完全恢复,损伤变量为零。弹性模量为常数,应力-应变曲线呈现线性关系。
在延性损伤阶段,塑性变形增大。在构件内部随着损伤不断累积,材料抗力减小,刚度呈现弱化,应力-应变曲线呈下降状态,应变增加的同时,应力不断降低。
3)损伤模型依赖三轴应力。模型具有以下特点:第一,损伤增长依赖静水压力和应变的增长。第二,采用弹塑性应变、静水压力同损伤演化模型相结合。

