基于T-S模糊神经网络的热负荷预测模型

姜 平 ，赵保国 ，张海伟 ，李丽锋 ，王鹏程 ，王欣峰 ，苑文鑫

(1.山西河坡发电有限公司，山西 阳泉 045001；2.山西大学自动化系，山西 太原 030006；3.山西大学数学科学学院，山西 太原 030006)

0 引言

为了满足“节能减排”、“双降双低”要求，热电联供系统的改造日益重要。而热负荷预测不管在研究供热需求方面，还是在研究供热机组调峰范围方面，对缓解热电机组供热和供电的矛盾都起着重要的作用。

热电联供系统热负荷的变化规律既包含一定的周期性，同时又具有随机性与不确定性等特点，所以热负荷的预测除了受自身的影响，一般还受外界诸多确定因素的影响[1]。目前，有大量的方法用于负荷预测，如灰色理论、时间序列、神经网络等[2]，而大部分的预测是以历史数据为基础的。文献[3]利用热负荷长期及周期性变化的特点，使用灰色理论来建立热负荷的预测模型，并提高了中期的预测精度。文献[4]通过研究数据的特征，利用长短时记忆(long short-term memory,LSTM)网络方法建立了居民供热负荷短期预测模型。该方法比传统预测方法精度更高。热电联供系统中热负荷的预测具有影响因素多，如循环水流量、室外温度、热网供水温度、热网回水温度等，且彼此间耦合性非线性较强，常规方法难以建立精确的数学模型。近年来，基于神经网络的强大的学习能力，以此进行热负荷预测的成果也越多[5-8]。模糊建模是一种建立复杂系统模型的方法，它能够以任意精度近似逼近复杂系统。神经模糊系统(neuro-fuzzy systems,NFS)结合了模糊逻辑和神经网络的理论，备受关注[9-12]。针对多维模糊推理中的推理规则庞大的问题，Takagi-Sugeno(T-S)模糊模型通过局部线性模型和模糊推理的数量来逼近复杂的非线性系统，具有良好的非线性逼近能力，广泛用于复杂非线性系统建模。本文采用T-S模糊神经网络(T-S fuzzy neural network，TSFNN)算法来建立热负荷预测模型，结构辨识部分采用基于减法聚类的模糊C均值聚类算法，参数辨识采用模糊神经网络的混合学习算法。

1 T-S模糊神经网络结构

1.1 T-S模糊结构

T-S模糊模型是由Takagi和Sugeno[13]提出的一种非线性模型，它将模糊理论与线性和非线性系统结合，实现以局部线性来描述全局非线性的方法。T-S模糊规则如下：

模糊系统的最终输出为：

(1)

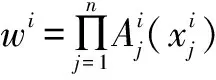
1.2 T-S模糊神经网络的体系结构

针对n输入单输出的T-S模糊神经网络，其中前件部分由六层组成，后件部分由三层网络组成。

第1层 输入层，每个神经元对应一个输入变量：

(2)

第2层 输入变量的隶属函数层，实现输入变量的模糊化，则输出为：

(3)

式中：Aij为语言术语；cij,σij分别为第i个规则下高斯隶属函数的中心和宽度。

第3层 “与”层，节点数与模糊规则数相对应：

(4)

式中：γi为学习过程中第i个规则下的补偿度。

第4层 该层进行输出的归一化：

(5)

第5层 T-S模糊神经网络的输出：

(6)

T-S模糊神经网络的建模分为结构辨识和参数辨识两部分[13-16]。本文利用基于减法聚类的模糊C均值算法进行结构辨识，进而划分输入输出空间。定义变量对应的模糊集及隶属函数，确定规则数目。参数辨识是通过模糊神经网络的混合学习算法，获得模型后件参数。

2 结构辨识

2.1 减法聚类

考虑M维空间的n个数据点(x1,x2,…,xn)，将每个点视为聚类中心的候选点，则数据点xi的密度指标定义为：

(7)

通过上式计算每个数据点的密度指标，从中选出最大的密度指标Dc1所对应的数据点xc1作为第一个聚类中心，去除这个数据点的密度再计算其他点的密度指标：

(8)

式中：ra、rb为预先设定好的领域半径，一般取rb=1.5ra。

2.2 模糊C均值聚类算法

根据减法聚类所确定的初始值C，将样本向量X=(x1,x2,…,xj,…,xn)T划分为C个模糊组，寻找各组的聚类中心，使模糊C均值聚类算法的性能指标最小。它的目标函数定义为：

(9)

式中：i=1,2,…,C;j=1,2,…,n;U=[μij]为C个模糊分区；V=(v1,v2,…,vC)T为聚类中心；C为模糊C均值聚类算法划分的聚类中心个数；n为输入样本的个数；m∈[1,∞]为加权指数；μij为xj在第i个规则下的隶属函数。

由拉格朗日乘子法构造新的目标函数：

(10)

分别对vi和μij求导，使目标函数最小值，其结果如式(11)、式(12)所示：

(11)

(12)

3 仿真

通过对热负荷的影响因素及实际情况进行分析，选取循环水流量(x1)、热网供水温度(x2)、热网回水温度(x3)、室外温度(x4)作为模型的输入变量，选取热负荷(y)作为模型的输出变量。

3.1 数据获取与处理

从热电厂分散控制系统(distributed control system,DCS)上采集过去连续两天48 h内的循环水流量x1、热网供水温度x2、热网回水温度x3、室外温度x4、热负荷y的144组历史数据，针对各变量单位及变化范围不同，对各变量的数据进行预处理[15]，归一化公式如式(13)所示：

(13)

式中：xN为变量x归一化后的值；xll为变量x的下限值；xul为变量x的上限值。

3.2 模型的建立与验证

将过去一天24 h的72组数据作为训练集，未来一天24 h内的72组数据作为检测集，进行热负荷的预测建模。本文选取x1(t-1)、x2(t-1)、x3(t-1)、x4(t-1)作为TSFNN的输入变量，将数据导入MATLAB平台中。

首先进行减法聚类，选取聚类半径r=0.5，阈值δ=0.15，通过减法聚类计算，各变量获得4个聚类中心。聚类中心如下：

模糊C均值聚类算法对初始值非常敏感，若初始值选择不当容易陷入局部最优的问题，所以引入减法聚类来确定模型的初始值。结合减法聚类的结果进行模糊C均值聚类，并将训练集划分为4个模糊组，选取指数权重m=2，经过31次迭代后，目标函数最小为1.413 374，最终获得72×4个隶属度函数。聚类中心如下：

对热负荷预测模型进行参数辨识，通过模糊神经网络的混合学习算法来确定后件参数，迭代次数为500，误差步长为0.001，最终获得后件参数如下所示:

将后件参数代入模糊规则中，具体如下所示。

R1：ifx1(t-1) isA11，x2(t-1) isA12，x3(t-1) isA13，x4(t-1) isA14,then

y(t)=-1.112+0.410 3x1(t-1) +0.518x2(t-1)+ 2.688x3(t-1)-1.121x4(t-1)

R2：ifx1(t-1) isA21，x2(t-1) isA22，x3(t-1)isA23，x4(t-1) isA24,then

y(t)=-0.437+0.836x1(t-1)+0.700 3x2(t-1)+1.583x3(t-1)-1.391x4(t-1)

R3：ifx1(t-1) isA31，x2(t-1) isA32，x3(t-1) isA33，x4(t-1) isA34,then

y(t)=-0.288 4+1.843x1(t-1)-0.192 5x2(t-1)+ 0.498x3(t-1) -0.632 2x4(t-1)

R4：ifx1(t-1) isA41，x2(t-1) isA42，x3(t-1) isA43，x4(t-1) isA44,then

y(t)=-0.425 7-0.779 7x1(t-1)-1.835x2(t-1)+ 0.969 6x3(t-1)-0.292 3x4(t-1)

则最终T-S模型输出为：

y(t)=-0.718 8+0.631 23x1(t-1)+0.505 37x2(t-1)+1.996 28x3(t-1)-1.213 27x4(t-1)

图1为T-S模糊神经网络训练集输出与实际输出曲线。从图1可以发现，两条输出曲线的变化趋势基本一致，且一些点基本与实际输出重合。为了分析预测输出的可信度，获得图2所示的训练样本相对误差分布曲线。其中：98%的样本点的相对误差在±0.4%之间，最大的误差小于6%，均方根误差为0.049 5，表明训练过程拟合度较好。

图1 T-S模糊神经网络训练集输出与实际值曲线

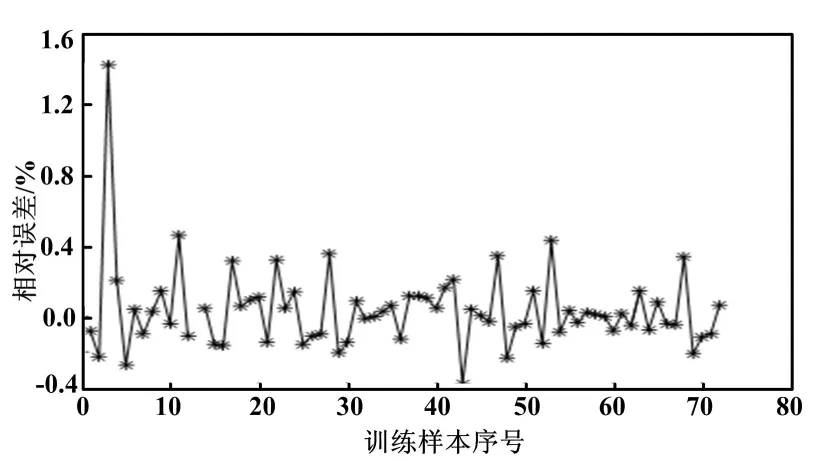
图2 训练样本相对误差分布图

为了进一步验证预测模型的合理性，对预测模型进行了检测校验，将第二天24 h的72组数据的输入变量导入上述模型中，并获得未来24 h热负荷的预测值。检测样本预测输出值与实际值对比曲线图3所示。个别点的预测值与实际值偏差较大，但热负荷的整体变化趋势一致。检测样本相对误差分布如图4所示。其中，98%的相对误差在±0.6%之间，最大误差小于0.8%，表明预测模型的拟合度精确度较好。

图3 检测样本预测输出值与实际值对比图

图4 检测样本相对误差分布图

4 结束语

准确预测热负荷的变化是解决火电厂供热和供电的矛盾和扩大机组调峰范围的重要基础。通过选取热负荷的几个主要影响因素作为输入变量，利用T-S模糊神经网络建立热负荷的预测模型。在MATLAB中进行训练，并对第二天的热负荷进行预测。结果表明：该TSFNN预测模型对热电联供系统热负荷具有较好的精确度和拟合度。基于该热负荷模型，可以深入开展热电负荷预测研究。这不仅有助于提高机组调峰能力，而且对于研究热量供需方面的问题至关重要。该方法可为上述研究提供理论依据。