一种建模不确定性的四旋翼无人机鲁棒跟踪控制

石振东,屈 蔷,程 陈

(南京航空航天大学 自动化学院,南京 211106)

1 引 言

近年来,四旋翼无人机备受关注,其以灵活性、垂直起降、自主悬停等优点被广泛应用于影视拍摄、军事侦察和交通运输等民用和军事领域[1].四旋翼无人机调节四个电机的转速完成平移和旋转运动,是一个四输入、六输出的欠驱动系统;在飞行过程中,四旋翼无人机不可避免得受到风等的影响,且其阻力系数和转动惯量无法精确测量,故四旋翼无人机系统是一个强耦合、参数不确定且容易受外部扰动的非线性系统,这使得四旋翼无人机轨迹跟踪控制困难[2,3].

关于四旋翼无人机系统的强耦合、欠驱动以及非线性问题,文献[4-6]引入虚拟向量,将四旋翼无人机闭环系统解耦为内环和外环子系统,这种内外环线性方法应用最为广泛,但是其解耦的条件严格,外环子系统需快速跟踪期望位置,否则会影响轨迹跟踪效果;文献[7-9]基于T-S模糊控制理论建立四旋翼无人机T-S模糊模型,设计T-S模糊控制器实现轨迹跟踪,这种T-S模糊模型可从任意精度逼近四旋翼无人机模型,其精度越高,模糊规则数量越多,大量的模糊规则会导致控制器难以获得,在实际的应用中难以实现.文献[10,11]在四旋翼无人机动力学模型的基础上,通过假设偏航角、俯仰角和滚转角均接近于0得到线性模型,设计了PID控制器并取得了良好的实验效果,这种线性化方法为后续的控制器设计降低了难度.

在飞行过程中,阻力系数会随四旋翼飞行环境发生变化,且绕三个坐标轴的转动惯量无法精确测量,这使得四旋翼系统存在不确定参数,一些文献针对这些不确定参数展开了研究.文献[6,12]利用自适应控制方法估计阻力系数,文献[13]利用神经网络的非线性逼近能力处理空气阻力的影响,但是文献[6,12,13]的控制器参数难以调节;文献[14]采用鲁棒补偿器抑制模型不确定性,这种不确定参数的处理方法较为复杂;文献[15]考虑了转动惯量在标称值±10%的情况,并设计鲁棒H∞控制器进行抑制,这种处理方法简单有效,鲁棒H∞控制器的求解可采用线性矩阵不等式(LMI)求解方法,直接通过矩阵运算获得,且其可抑制外部扰动.基于此,本文采用鲁棒H∞控制器处理不确定的阻力系数和转动惯量,并对外部扰动进行抑制,增强四旋翼无人机系统的鲁棒性.

本文针对四旋翼Qball2模型中参数不确定性的问题提出了一种鲁棒H∞跟踪控制方法.首先,建立四旋翼无人机X通道、Y通道、Z通道的误差系统;然后,考虑到飞行环境变化引起的阻力系数的不确定性、转动惯量的不确定性以及外部扰动,对X通道、Y通道和Z通道设计了鲁棒H∞反馈控制器进行抑制并跟踪参考轨迹;最后,根据李雅普诺夫稳定性定理得到使X通道、Y通道和Z通道闭环系统渐进稳定且满足H∞性能指标的LMI充分条件.与内外环鲁棒反馈控制器的仿真结果证明了所提方法的优越性和鲁棒性.

2 四旋翼无人机模型与预备知识

图1为四旋翼无人机的结构图,F1、F2、F3、F4表示旋翼升力;惯性坐标系I=(ix,iy,iz)原点固定于地面,iz轴垂直于地面指向天空;机体坐标系B=(Bx,By,Bz)以四旋翼无人机质心为原点,以支架为坐标轴;x(t),y(t),z(t),φ(t),θ(t),ψ(t)表示四旋翼无人机的6个自由度.

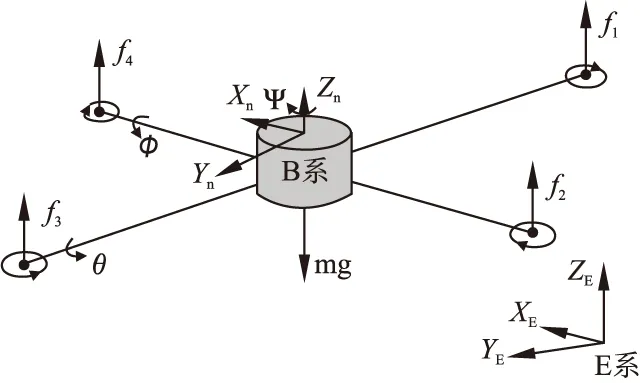
图1 四旋翼无人机示意图Fig.1 Four rotor UAV structure diagram

假设四旋翼无人机结构对称,根据文献[4-6],四旋翼无人机的动力学模型为:

(1)

(2)

(3)

(4)

(5)

(6)

式中,m为四旋翼无人机的质量,Ki(1,2,3,4,5,6)表示空气阻力系数,Jφ、Jθ、Jψ表示转动惯量,g为重力系数,c为力与力矩比例系数,l表示四旋翼无人机质量中心到旋翼轴心的距离,旋翼升力建模如公式(7-8):

(7)

(8)

式中ui为第i个电机的PWM输入;K为正常数;vi为电机状态量;ω表示带宽.

控制输入uz、uφ、uθ、uψ如下:

下面给出本文需要用到的假设及引理.

假设1.外部扰动‖dx‖≤ζ1,‖dy‖≤ζ2,‖dz‖≤ζ3,‖dφ‖≤ζ4,‖dθ‖≤ζ5,‖dψ‖≤ζ6,这里ζ1、ζ2、ζ3、ζ4、ζ5、ζ6为未知正常数.

引理1.假设X和Y为合适维数的实矩阵,对于任意给定的正常数α,有下列不等式成立:

XTY+YTX≤α-1XTX+αYTX

引理2.对任意给定的分块对称矩阵：

其中X和Z为对称矩阵,则下述情况等价:

1.G<0

2.X<0,Z-YTX-1Y<0

3.Z<0,X-YZ-1YT<0

3 鲁棒H∞控制器设计

这一部分的主要内容为建立四旋翼无人机X通道、Y通道、Z通道的线性误差模型和设计鲁棒H控制器.

3.1 误差模型

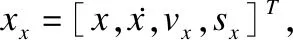
(9)

其中:

Δ表示线性化不确定性.

为了实现X通道的跟踪控制,令xd表示期望位置x,θd表示期望俯仰角;选择参考模型如公式(10):

(10)

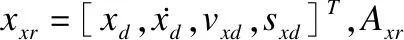
假设2.存在矩阵K12,K13使得Axr和Bxr满足Axr=A1+B11k13,Bxr=B11K12.

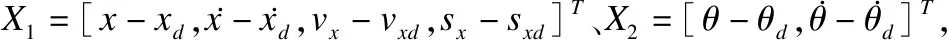
(11)

X2=A2X2+B21(U2+Fθ)+B22W22

(12)

其中：

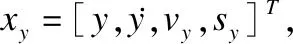
xy=A3xy+B31U3+B32W3

(13)

其中:

为了实现Y通道的跟踪控制,令yD表示期望位置y,φD表示期望滚转角;选择参考模型如公式(14)：

xyr=Ayrxyr+Byrry(t)

(14)

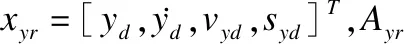
假设3.存在矩阵K32,K33使得Ayr和Byr满足Ayr=A3+B31K33,Byr=B31K32.

X3=A3X3+B31(U3-K33xyr-K32ry)+B32W3

(15)

X4=A4X4+B41(U4+fφ)+B42W4

(16)

其中：

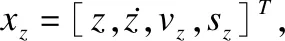
xz=A5xz+B51U5+B52W5

(17)

其中:

为了实现Z通道的跟踪控制,令zD表示期望位置z,ψD表示期望偏航角,选择参考模型如公式(18):

(18)

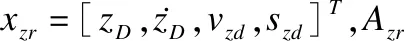
假设4.存在矩阵K52,K53使得Azr和Bzr满足Azr=A5+B51K53,Bzr=B51K52.

(19)

(20)

其中:

3.2 鲁棒反馈控制器设计

对X通道、Y通道和Z通道误差模型设计如公式(21-26)的鲁棒状态反馈控制器:

U1=K11X1+K12rx+K13xxr

(21)

U2=K21X2-fθ

(22)

U3=K31X3+K32ry+K33xyr

(23)

U4=K41X4-fφ

(24)

U5=K51X5+K52rz+K53xzr

(25)

U6=K61X6-fψ

(26)

其中,Ki1(i=1,…,6)、Kj2(j=1,3,5)、Kk3(k=2,3,6)是控制增益矩阵.

误差模型(11、12)、(15、16)和(19、20)在控制器(21-26)作用下的闭环系统为:

Xi=(Ai+Bi1Ki1)Xi+Bi2Wi

(27)

可以得到如下定理:

定理1.对于给定正常数γj(j=1,3,5),γk(j=2,4,6),如果存在实对称正定矩阵Qi、正常数εj,εk和矩阵Mi使得下面的LMI成立:

(28)

(29)

那么,闭环系统公式(27)渐进稳定且满足H性能指标γi,有其中

证明:假设Wi≡0,选取李雅普诺夫函数:

(30)

上式对时间求一阶导数,并将公式(27)代入可得:

(31)

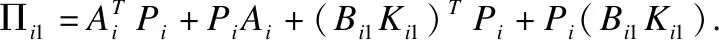
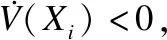
在闭环系统(27)渐进稳定且扰动Wi≢0的情况下,对于给定正常数γi,考虑H性能指标如公式(32):

(32)

因为闭环系统(27)渐进稳定且系统初始条件为零,可得:

(33)

式中：

如果Πi2<0,那么Ji<0,则闭环系统(27)满足H性能指标γi.

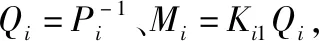
(34)

闭环系统(27)中不确定参数Ki(i=1,…,6)、Jφ、Jθ、Jψ、Δ使得矩阵Ai、Bk1(k=2,4,6)中存在不确定性,表示为Ai=Ai0+ΔAi、Bk1=Bk10+ΔBk1.根据文献[14],ΔAj和ΔBk1可表示为:

ΔAj=DjFj(t)Ej1(j=1,3,5)

(35)

(36)

将公式(35),公式(36)代入公式(34)得:

(37)

(38)

其中：

根据引理3,公式(37),公式(38)等价于：

(39)

(40)

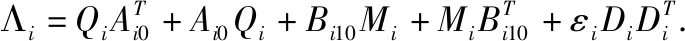
定理1证明完毕.

4 仿真结果

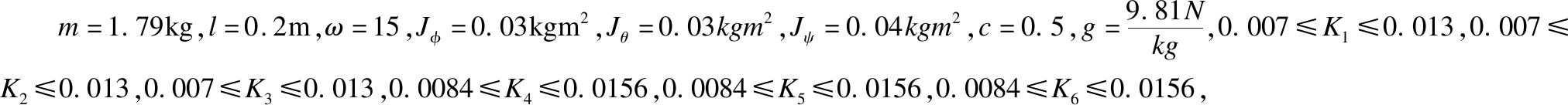
Bxr=[0 0 15 0]T

Byr=[0 0 15 0]T

Bzr=[0 0 15 0]T

根据文献[14]选择

D2=[0 1]T;E21=[0 0.035];

E22=[3.3];D3=D1;E31=E11;

D4=D2;E41=E21;E42=E22;

D5=D1;E51=E11;D6=[0 1]T;

E61=[0 0.12];E62=[0.012].

采用Matlab的LMI工具箱求解定理1中的LMI式(28)和式(29),取γi=1得到:本文所设计的控制增益矩阵:

K11=[-3.1776 -1.9347 -0.1470 -1.7115];

K12=[1];

K13=[-0.2667 -0.2000 0.6667 -0.4667];

K21=[-0.6606 -1.1824];

K31=[3.1776 1.9347 -0.1470 1.7115];

K32=[1];

K33=[0.2000 0.1333 0 0.0667];

K41=[-0.6606 -1.1824];

K51=[-8.0985 -5.8026 -0.0162 -4.7980];

K52=[1];

K53=[-0.2667 -0.2667 -0.7667 -0.0333];

K61=[-3.0855 -4.2142].

Case1,选取rx(t)=ry(t)=sin(0.1t),rz(t)=t可得图2所示的期望轨迹图.

与内外环鲁棒反馈控制进行仿真对比,控制器增益如公式(40-41)所示,相应的位置跟踪误差和角度跟踪误差曲线如图3-图4所示.

(41)

(42)

图3 case1下的位置跟踪误差
Fig.3 Position tracking error under case1

从图3可知,采用内外环鲁棒反馈控制器的最大X向跟踪误差为0.048m,而采用本文方法的最大跟踪误差为0.013m;在Y方向,采用内外环鲁棒反馈控制器的最大跟踪误差为0.053m,而本文方法的最大跟踪误差为0.018m;采用内外环鲁棒反馈控制器的最大z向跟踪误差为0.36m,而采用本文方法的最大跟踪误差为0.01m.可知本文提出的控制方法位置跟踪误差更小.从图6可以看出,采用本文方法的角度跟踪误差小于内外环状态反馈控制器.因此,本文所提出的控制方法比内外环鲁棒反馈控制器的控制效果更好.

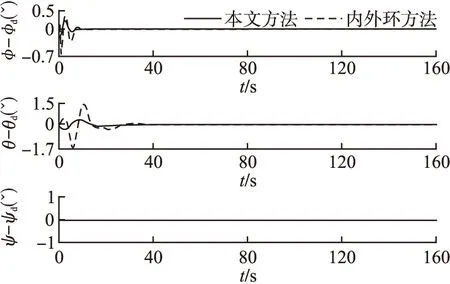
图4 case1下的角度跟踪误差Fig.4 Angle tracking error under case1

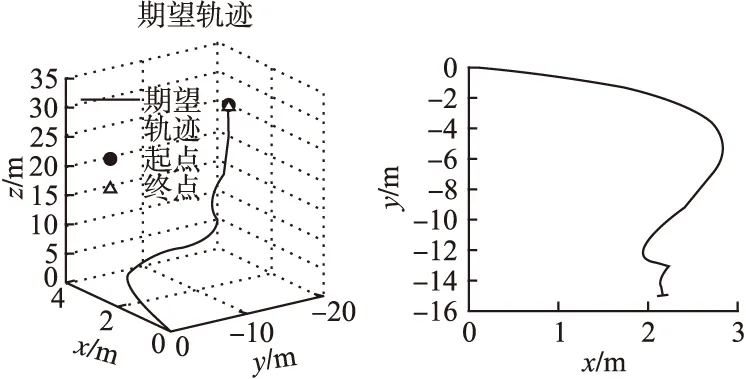
图5 case2下的期望轨迹图Fig.5 Expectation trajectory under case2

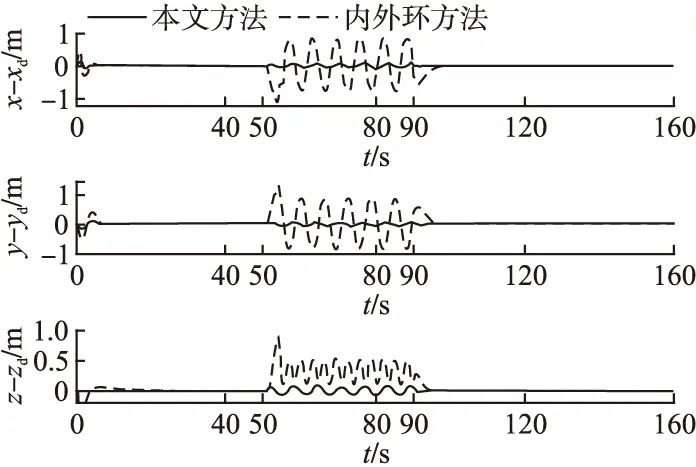
图6 case2下的位置跟踪误差Fig.6 Position tracking error under case2

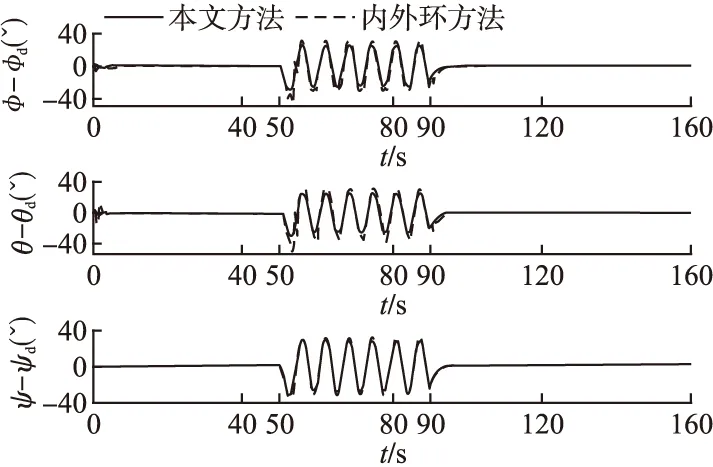
图7 case2下的角度跟踪误差Fig.7 Angle tracking error under case2

Case2,为了验证本文方法的鲁棒性,在50s-90s之间加入扰动:dx=dy=dz=0.2sint,dφ=dθ=dψ=0.12sint,选取rx(t)=ry(t)=rz(t)=t,可得图5所示的期望轨迹图.在此条件下,内外环鲁棒反馈控制器和本文控制方法仿真的跟踪误差如图6-图7所示.

从图6-图7可以看出,外部扰动的作用时,采用本文方法的位置误差和角度跟踪误差均明显小于内外环鲁棒反馈控制器.所以本文方法设计的控制器抑制外部扰动的能力更强.

5 结 论

本文研究了具有参数不确定性的四旋翼无人机系统,建立了X通道、Y通道和Z通道线性误差系统,在此基础上设计了鲁棒H∞跟踪控制器跟踪期望轨迹,并与内外环鲁棒反馈控制器进行对比仿真,仿真结果验证了所提出方法的优越性和鲁棒性.