对时差无源定位系统的相干干扰技术

陈 慧，李 昊

(中国电子科技集团公司第三十八研究所，安徽 合肥 230088)

0 引 言

时差无源定位由于具有较好的隐蔽性和精确性,应用广泛，如捷克的“维拉”系列、俄罗斯的“卡尔丘塔”地基无源定位系统[1]，以及美国海军“白云”星座电子情报侦察系统、天基广域监视系统等，都采用了多站时差定位技术体制对目标辐射源进行无源定位。特别是美军电子情报侦察卫星具有全天候、全空域的电子侦察监视能力，两小时内可对全球任一区域监测一次[2]。传统雷达主要采用被动措施对抗电子侦察，如无线电静默、波束控制、功率控制等[3],但被动防护严重影响了己方装备作战效能的发挥，需要研究有源对抗的积极手段来予以应对。

1 相关处理在时差无源定位系统中的应用

根据多站时差无源定位系统的特点和要求,满足定位的前提条件是3个或以上侦察站能够同时侦收到同一部雷达辐射源发射的同一个脉冲信号,根据信号到达不同站的时差信息来对目标辐射源进行双曲线定位。在时差无源定位精度要求基线保证一定的长度、多站同时覆盖同一片区域、各站侦察天线保证一定的波束宽度等客观要求下，各站同时能够侦收到辐射源波束的主瓣信号的概率较小。特别是针对当前广泛应用的阵列天线窄波束雷达的侦察,因此侦察单站必须具备副瓣侦收的能力,时差无源定位系统必须具有较高的侦察灵敏度。

传统的侦察系统为了提高接收机灵敏度而采取的方法在无源定位系统中难以应用,如通过降低接收机噪声系数对接收机灵敏度的改善意义不大，甚至导致成本的增加；减小接收机带宽会牺牲接收机的截获概率和侦收的信号能量，并导致脉冲波形失真进而影响脉冲到达时间(TOA)的测量；匹配接收需要知道所接收信号的信息结构,这在非协作方式的电子战环境中是难以实现的[4]。由于时差无源定位系统各站侦收的目标信号来自于同一辐射源，信号具有相关性，而大部分噪声是独立随机的，因此时差无源定位系统多采用多站相关处理的方法来解析信号并测量脉冲到达时差信息。

对于平稳随机信号x(t)和y(t)，其互相关函数可以表示为：

Rxy(τ)=E[x(t)y(t-τ)]=

(1)

在实际中常需在有限的时间内计算互相关函数的估计值，如在主站、副站和目标辐射源构成的几何三角关系中，有三角不等式：

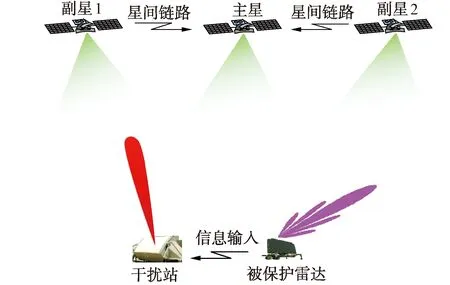
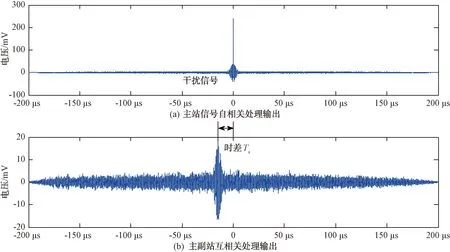
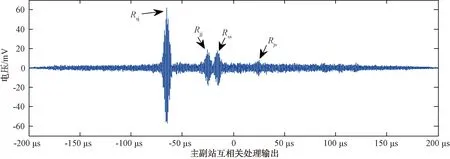
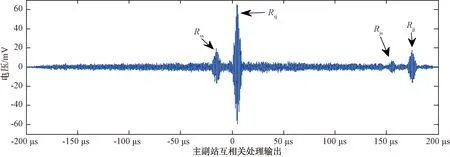
0

(2)

式中：d表示主、副站间的基线长度。

真实到达时差是在一定的范围内，这个范围与主站到副站的距离有关且必须满足上式，通过上式的限制可以降低匹配时的数据量，即在限制的时间范围内选取数据进行互相关处理[5]。

副站将侦收到的信号转发给主站，2路信号之间表现为纯延时的特性，可用互相关法测量延迟的时间。假设x(t)经过延时T得到另一路信号：y(t)=Ax(t-T)，则互相关处理后为：

Rxy(τ)=E[x(t)y(t-τ)]=

E[x(t)x(t-T-τ)]=Rxx(τ+T)

(3)

可见，互相关处理后即为自相关函数，只不过峰值较原自相关函数发生了偏移，偏移值即为测量时差T。

因此采用互相关信号匹配法，能够有效地抑制不相关的噪声干扰，提高检测信噪比；与此同时还能够较准确地测得2路通道间的信号时差，甚至在同时存在多个不同频率等参数的信号时也可以一并处理检测出时差信息，避免了微弱信号条件下的信号检测、参数测量等问题，因此相关处理在时差无源定位系统中被广泛应用。

2 对时差无源定位系统的相干干扰

由于时差无源定位系统采用相关处理技术，能够很好地抑制不同通道间相互独立的接收噪声，但对于多站共同覆盖区域内同一个噪声源信号，由于具有相关性，通过相关处理是无法抑制掉的，并且还有处理增益，因此对时差无源定位系统传统的干扰方法主要采用噪声，如有源噪声调频干扰[6]，利用来源于同一噪声信号的相关处理增益去恶化检测信噪比。但噪声干扰也存在很多问题，主要表现在同一噪声源信号自相关处理后波形特别窄、积累高，而脉冲信号自相关处理后波形展宽，和噪声自相关波形明显不同；另外由于时差不同，在经过相关处理后，噪声干扰信号的波形增益峰值和被保护目标信号的波形增益峰值位置不一致，时域上达不到遮盖的干扰效果。相关处理时，被保护目标脉冲信号和干扰噪声信号因独立而各自相关得到增益，相互之间影响不大。

2.1 对时差无源定位系统的相干干扰模型

噪声干扰不能影响对被保护目标信号的相关处理增益，但若采用与被保护目标信号具有相干性的干扰信号，就可以破坏多站间对目标信号的相关处理结果，造成相关失配，形成欺骗时差信息。因此提出针对时差无源定位系统的相干干扰方法，其战术配置如图1所示。

图1 对时差无源定位系统的相干干扰配置示意图

干扰站部署在距离被保护雷达一定范围，既便于接收并转发雷达发射的信号，又不至于干扰到雷达的正常工作。干扰站通过通信或者侦察手段，接收雷达发射的信号，再存储、调制、发射出去，对时差无源定位系统形成转发干扰。时差无源定位系统各站大概率侦收目标雷达波束的副瓣信号，而干扰站即使在窄波束情况下，也可以对其中的某个侦察站实施主瓣干扰，因此在干信比上能够容易满足要求。

以其中一主一副两站为例，假设主侦察站直接侦收被保护雷达的信号为xs(t)=Azsx(t)，则通过副站转发侦收的雷达信号为ys(t)=Afsx(t-Ts)；主侦察站直接侦收的干扰站转发的干扰信号为xj(t)=Azsx(t-ΔT)，通过副站转发侦收的干扰信号为yj(t)=Afjx(t-ΔT-Tj)，其中Ts为主、副站侦收目标雷达信号的时差，Tj为主、副站侦收干扰信号的时差，ΔT为干扰站转发雷达信号的延时。则主站将侦收的主、副两路信号X(t)=xs(t)+xj(t)、Y(t)=ys(t)+yj(t)进行相关处理得：

RXY(τ)=E{[xs(t)+xj(t)][ys(t-τ)+

yj(t-τ)]}=Rss(τ)+Rsj(τ)+

Rjs(τ)+Rjj(τ)

(4)

其中不难得出：

(5)

从上可以看出，2路相关处理的输出结果中包含了4个成分：主副路侦收的雷达信号自相关输出Rss(τ)、主副路侦收的干扰信号自相关输出Rjj(τ)、主路雷达信号和副路干扰信号互相关输出Rsj(τ)、主路干扰信号和副路雷达信号互相关输出Rjs(τ)，相关处理输出的波形取决于这4个部分的占比，如果能尽量降低雷达信号自相关输出Rss(τ)所占的比重，就可以达到干扰抑制目标定位的效果。

2.2 信号功率对相关输出波形峰值位置的影响

由于采用转发式干扰，干扰信号和雷达信号除了信号功率、时间延时不同外，可以忽略其它参数的不同，因此主副路相关处理后的输出波形仅与4个信号的功率、时间延迟有关，其中信号功率的相对大小影响相关输出波形主峰的位置，也就是判断时差偏移的位置：

(1) 当max(Azj，Afj)≤min(Azs，Afs)时，相关后Rss(τ)最大，信号时差信息还能提取，干扰无效；

(2) 当min(Azj，Afj)≥max(Azs，Afs)时，相关后Rjj(τ)最大，目标被定位到干扰站上；

(3) 当Azj>Afs≥max(Afj，Azs)时，相关后Rjs(τ)最大，峰值转移，时差信息提取错误，干扰有效；

(4) 当Afj>Azs≥max(Azj，Afs)时，相关后Rsj(τ)最大，峰值转移，时差信息提取错误，干扰有效；

(5) 当min(Azj，Azs)≥max(Afj，Afs)或min(Afj，Afs)≥max(Azj，Azs)时，即在同一路出现2个信号同时大、同时小的情况，相关后Rss(τ)、Rjs(τ)、Rsj(τ)、Rjj(τ)的值被均匀、大小区分不明显，Rss(τ)不一定能呈现绝对的优势，也会导致不能检测出目标信号的时差信息。其中当Azj=Azs且Afj=Afs时，Rss(τ)=Rjs(τ)=Rsj(τ)=Rjj(τ)，形成4个等高峰值波形。

从以上分析可以看出，要对时差无源定位系统进行有效干扰，2路接收通道中干扰信号功率至少要比其中一路目标雷达信号的功率强，但2路均为干扰信号功率最强的情况也会导致干扰站被稳定定位。理想的情况是：其中一路接收的干扰信号和另外一路侦收的雷达信号来相关处理并获取得到最大增益，即相关失配，来欺骗定位系统提取错误的时差信息，造成定位错误，也即(3)、(4)中的情形。

2.3 干扰信号延时对相关输出波形峰值位置的影响

在瞬时空间相对位置确定的情况下，信号接收、转发的时差是固定的，即Ts、Tj值是固定的。因此对(1)、(2)中的情形，由公式(5)可以得出无源定位系统对目标雷达或干扰站的定位是确定的、不可更改的；但对于(3)、(4)中的情形，根据失配相关计算公式：

(6)

可以看出，失配相关输出峰值Rjs(τ)、Rsj(τ)的位置除了和相对固定的Ts、Tj有关系外，还和转发延时参数ΔT有关系，而该参数除了和干扰站及被保护雷达之间的距离、信号转发延时等有关外，还可以通过数字射频存储器(DRFM)来控制延时量，以产生不同时差信息、不同位置辐射源的欺骗干扰。延时拖引干扰的过程可以是线性连续的，欺骗产生运动辐射源的轨迹；也可以是动态离散的，造成时差无源定位系统对目标定位的随机跳跃，无法形成稳定的固定地点或者运动轨迹。

3 仿真实验

以一主一副两站间的相关处理为例，假设干扰站距离被保护雷达12 km，时差无源定位系统主副站基线长度为50 km，雷达、干扰站位于无源定位系统偏正前方；扣除基线延时，设置时差Ts=15 μs、Tj=25 μs；侦察站中频处理后的目标信号中频频率为50 MHz，脉冲重复周期为200 μs，脉宽为5 μs；为了便于观察，设置主副路侦收的目标雷达信号信噪比分别为9 dB、1 dB，主副路侦收的干扰信号信噪比分别为-1.4 dB、12 dB。在采样时间满足T<2d/c的情况下，不失一般性，以1个脉冲重复周期内采样为例，进行相关处理。

图2分别是主站和副站侦收到的被保护雷达信号和干扰信号时域波形图，其中主站接收到的干扰信号和副站接收到的雷达信号信噪比相对较低，波形不明显。在没有干扰的情况下，时差无源定位系统只侦收到雷达信号，进行主副站相关处理提取时差信息，原理过程如图3所示，时差Ts可通过2路信号的自相关和互相关来测得。

图2 主、副站侦收的信号波形图

图3 无干扰时相关时差测量原理图

图4 干扰时相关时差测量波形图(ΔT=40 μs)

当施加干扰后，2路信号经过相关处理，分别积累得到4个处理增益，信号强度满足情况(4)的条件，其中Rsj(τ)增益最大，会导致时差无源定位系统将Rsj(τ)误判为Rss(τ)，特别是在低信噪比的弱信号侦察的情况下，其它3个峰值相比于噪声并不明显，导致时差测量、无源定位错误，如图4所示。根据公式(6)，增大转发干扰延时ΔT的值，会导致Rsj(τ)峰值位置发生偏移，时差测量误差增大，如图5所示。

当进一步控制加大干扰延时ΔT=170 μs时，副站干扰脉冲信号进入下一重复周期(加上干扰信号到达副站与主站的时差25 μs、主站雷达信号到达时间在10 μs位置)并领先下一周期的主站雷达信号，相关处理后出现Rsj(τ)向自相关中心右偏的情况，即副站干扰信号领先主站雷达信号，如图6所示。

图6 干扰时相关时差测量波形图(ΔT=170 μs)

继续增大干扰延时，峰值继续左移，当干扰延时ΔT超过重复周期200 μs后，上述干扰过程周期性重复出现。由此可见，合理控制干扰延时，就能够控制产生假目标欺骗时差信息，甚至还能产生超前到达时差，进而模拟不同位置的假目标辐射源。

4 结束语

通过对时差无源定位系统的相干干扰分析，可以为反电子侦察提供一些参考思路。转发式干扰是实施相干干扰的最佳途径，另外由于相关处理对信号相位的要求不是很严格，也可以在确保知悉雷达信号载频变化规律的先验信息前提下，干扰站自身产生非相干干扰，实验证明只要频率偏差在1%以内，同样能实现针对相关处理的干扰。这里需要注意的是，针对时差无源定位系统的相干干扰的前提条件是重点干扰多站中的一个侦察站，造成该站侦收的干扰信号和其它站侦收的雷达信号失配相关，而不是同时干扰所有站，导致干扰站被定位。在干扰天线设计上可采用阵列天线窄波束，战术上可将波束对准其中的一个侦察站，如干扰一边的副站，即可达到相干干扰的要求。