RDX的爆炸产物组成和爆热的计算与分析

张金龙,郭子如,杜明燃,李 国

(安徽理工大学化学工程学院,安徽淮南232001)

0 引言

黑索今(RDX)、梯恩梯(TNT)等烈性高能CHON 类炸药在军工及其它方面应用广泛,深入认识和理解该类炸药的起爆性能、爆轰能力等是有意义的。 炸药的各类爆轰参数是广大研究者衡量炸药性能的重要参考标准,爆轰参数在很大程度上取决于炸药爆热的大小。 探讨炸药爆热的计算方法以及了解采用哪种方法更接近实际场景的爆轰参数具有一定实际价值。

本文应用已有的爆轰产物组成的经验确定方法,运用盖斯定律计算出RDX 的爆热,引用了学者吴雄等的VLW 计算代码得出的爆轰产物组成,并计算了爆热,对上述计算结果进行了分析比较,同时与文献中得到的RDX 的爆热计算或实验测定值亦进行了比较,并进行了讨论。

1 爆炸化学反应方程式的确定和爆热计算[1-5]

计算炸药爆热由热化学方法、爆热经验计算方法和量子化学法。 而最常用的是热化学方法。 首先确定爆炸产物的组成,然后按照盖斯定律计算爆热。 确定爆炸产物组成的方法主要有经验法和理论计算方法两大类。

爆炸产物组成的理论确定方法是采用某种适当的爆轰产物状态方程,运用经典的化学平衡原理和爆轰化学反应的质量守恒原理进行产物组成确定。 理论计算方法较为复杂,一般需要借助计算机编码来实现。 理论方法科学原理强,因而可信度高。 已经公认的经验方法有 Li-Chatelier(简称LC)方法、Brinkly-Wilson ( 简称B-W ) 方法和最大放热量规则。

1.1 L-C方法

该方法以最大爆炸产物体积为原则,是在体积相同的情况下,侧重于放热多的反应。

对第一类炸药(c≥2a+0.5b) ,由于O 含量充足,C、H 两种元素被完全氧化为CO2和H2O,并生成分子状态的N2,剩余的氧元素也被氧化为O2。

对第二类炸药(a+0.5b≤c≤2a+0.5b),首先考虑对生成气体产物有利的反应,C→CO。 余下的O 平均分配,用于生成CO2和H2O。

而对于第三类炸药(c＜a+0.5b),由于严重负氧,L-C 规则并不适用。 我们采取改进方法。 先将3/4H 氧化成H2O,再将剩余的氧平均分配用于氧化C,使之生成 CO2和 CO,显然 CO 的摩尔数是CO2的两倍,且有固体碳生成。 爆炸反应方程式如下:

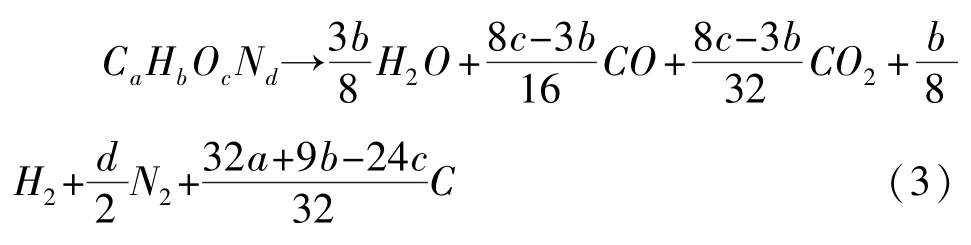
当以上各化学计量数为零或负值时,该项省略。

1.2 B-W规则

布伦克里和威尔逊的计算方法遵循能量优先原则,满足H2O→CO→CO2的产物生成顺序。 该类方法优先将炸药中的H 元素全部与O 元素结合,生成H2O。 剩余的O 再将炸药中的C 完全氧化成CO,如果仍然剩余O,则全部用于生成CO2,如果O含量不足,剩余的C 元素,以C 单质形式保留。 炸药中的N 元素则默认生成N2。

对第一类正氧平衡炸药(c≥2a+0.5b),爆炸反应方程式与L-C 方法相同,这里不再赘述。

对负氧平衡第二类炸药(a+0.5b≤c≤2a+0.5b), O 元素在完全氧化H 元素之后,全部用于生成CO。 完整的爆炸反应方程式如下:

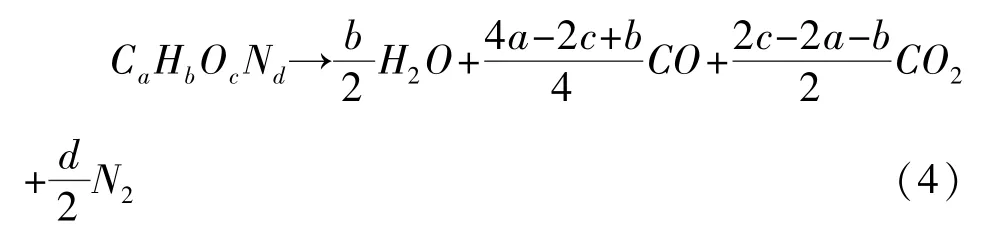
对第三类严重负氧炸药(c＜a+0.5b),O 元素在完全氧化H 元素之后,不足以将C 元素完全氧化,故有C 单质生成。 爆炸反应方程式如下:

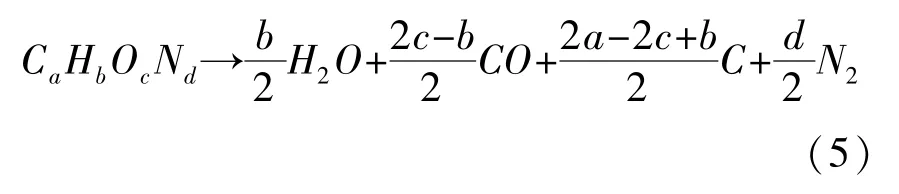
该爆炸反应方程式满足0.5b≤c＜a+0.5b

1.3 最大放热量规则

该类方法即 H2O→CO2方法。 先将 H 元素氧化成H2O,再将C 元素氧化生成CO2,而不生成CO(针对负氧平衡炸药)。 对于CHON 型炸药,爆炸的产物组成与 CO 反应生成 CO2和 C、H2与 CO 生成H2O 和C 的两个反应有极大关联。

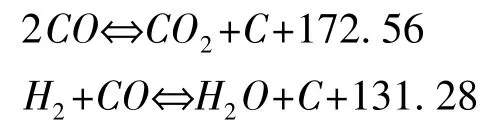
可以得到最终负氧平衡(c≤2a+0.5b)的炸药爆炸反应方程式为:

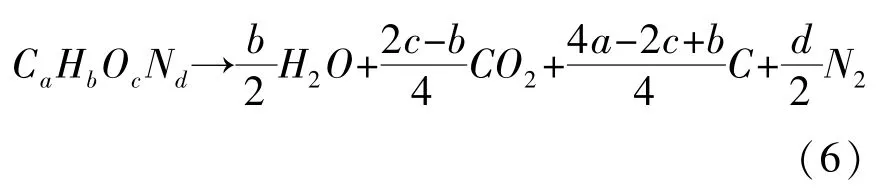
该爆炸反应方程式满足0.5b≤c＜2a+0.5b

1.4 VLW状态方程

二十世纪八十年代, 吴雄等人以维里(VIRIAL)理论为基础建立了爆轰产物状态方程(VLW EOS),又于九十年代在理论上加以完善,历经三十多年的应用考察,证实了采用该状态方程和相应的计算机编码计算可以很好的计算还原炸药爆轰产物组成。

该爆轰产物状态方程形式如下:

式中:B*(T*)为无量纲第二维里系数,T*为无量纲温度,方程具体内容,可参照文献[6]。 依据该状态方程可以理论计算出爆轰产物组成和爆轰参数。

2 爆热计算参数及比较

2.1 爆热参数计算方法

采取理论计算方法进行计算。 遵循化学反应过程中,体积恒定或者压力恒定,且系统没有做任何非体积功时,化学反应热效应只取决于反应的初态和终态,与反应的具体路径无关的规则,即盖斯定律。

爆轰产物的生成,只能由两种方法得到。 一是由各类元素的稳定单质直接反应得到,二是通过稳定单质生成的炸药发生爆炸反应后得到。

我们将稳定单质直接生成爆轰产物所释放的热量定为Q1.3,炸药爆炸反应过程所放出的热量定为Q2.3,元素的稳定单质生成炸药所放出或者吸收的热量定为Q1.2。

则按照盖斯定律对以上三者有如下关系式:

2.2 爆轰产物组成

以1 kg 炸药为基准,运用经验确定的爆轰产物组成以及参考文献[6]运用VLW 爆轰产物状态方程理论计算的RDX 的爆轰产物组成(mol/kg)见下表1。

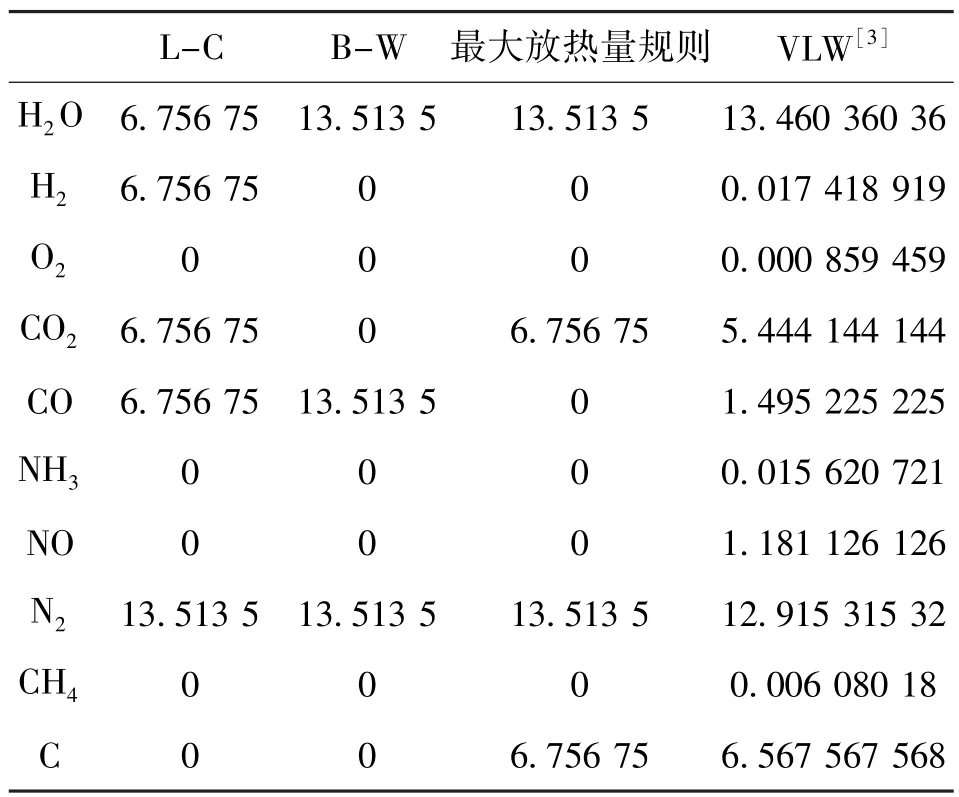
表1 爆轰产物组成

2.3 VLW方程与经验算法得到的爆热计算结果的比较

根据表1 爆轰产物的组成,通过盖斯定律计算得出四种方法的RDX 爆热数据及相对比值如下表2。

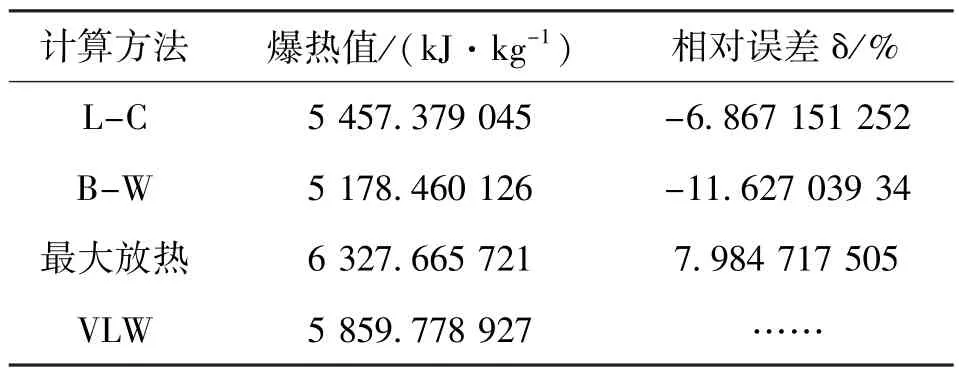
表2 RDX 的计算爆热

表中相对误差是以VLW 方法得到的爆热值为基准(真值)得到的。

2.4 文献中爆热值与经验算法结果比较

为进一步分析讨论,参考多篇文献中的RDX爆热数据。

本文所参考的文献[7]中的RDX 爆热值是文献作者在测试铝成分对RDX 炸药性能研究时所做的空白组对照试验,具体爆热的试验方法参照GJB 772A-97。

本文所参考的文献[8]中的RDX 爆热值是文献作者对含铝炸药进行研究时所做的空白组试验。试样采用圆柱形压装RDX ,并投入了5%的黏结剂。 药柱的长径比为(1.0 ～ 1.2) ： 1.0。 一端带雷管孔。 黏结剂的组分(质量分数 ) 为 1.5%F2603、3%蜡和0.5% 石墨。 试样质量为25 g,采用8 号铜电雷管端面起爆。

本文所参考的文献[9]中的RDX 爆热值是运用KHT(Kihara-Hikita-Tanaka)程序得到 RDX 的p-v 等熵数据,并采用非线性拟合软件1stOpt 的差分进化法在部分公式的约束下,对 JWL(Jones-Wilkins-Lee)状态方程进行参数的预测。 KHT 程序则是由以炸药组分出发、以混合产物自由能最小的原理找出最佳的爆轰产物组成的KHT 状态方程采用FORTRAN 语言编制而成的。 具体计算方法可参考文献[6]。

本文所参考的文献[10]中的RDX 爆热值测定所采取的试验装置为:绝热型爆轰量热计。 采取的试验方法为:将固体试样压成直径25 mm 的药柱,并在上端开有直径7 mm、深15 mm 的雷管孔,在精确称量后放入直径25 mm、壁厚8 mm 的陶瓷外壳中,并接好铜壳电雷管悬挂在弹盖下方;在改好弹盖之后抽真空并充入高纯氮至1.5 MPa,然后放空高纯氮再抽真空,然后得到的试验值。

本文所参考的文献[11]中的RDX 爆热值是在研究炸药密度与炸药爆热的关系时,引用文献[12]中炸药密度与爆热的关系式所得到的不同炸药密度下的炸药爆热。 由文献[11]中RDX 所对应的爆热值随密度增大缓缓上升可知,RDX 的最大爆热应略高于密度1.50 g/cm3时的5 401 kJ / kg 的爆热值,接近L-C 法所得到的5 458 kJ / kg,但仍远低于最大放热规则所计算的6 328 kJ / kg。

本文所参考的文献[13]中的RDX 爆热值是文献作者在精确建立爆轰参数隶属函数时为研究各炸药相对TNT 所对应的隶属函数值所引入的常见单质炸药爆热值。

本文所参考的文献[14]中的RDX 爆热值是文献作者在利用主成分分析法研究炸药5 大爆轰参数(爆热、爆速、爆压、爆容、爆温)对炸药性能影响的相关系数大小所引用的常见单质炸药爆热值。结果如下表3。

其相对误差之比如下表4。

表3 其他文献RDX 爆热值

表4 经验算法与其他爆热值的相对误差%

由表4 可以发现,各参考文献中(除文献[9])爆热值均最为接近L-C 法所计算得到的RDX 爆热值,且文献[9]中爆热值与L-C 法及最大放热规则所得到的爆热值相对误差的数值接近,也可一定程度说明L-C 法的优越性。

3 结论

1)在利用爆轰产物经验算法计算RDX 的爆热时,最大放热规则得到的爆热值最大,B-W 法得到的爆热值最小,

2)L-C 法在理论运用中所计算得到的RDX 爆热较其余两种方法更接近VLW 状态方程得到的爆热值。

3)最大放热量规则所得到的爆轰产物组成比例最接近VLW 状态方程所得到的爆轰产物组成比例。

4)通过让经验算法得到的RDX 爆热值与多个参考文献中的RDX 爆热值相比较可知,采用L-C法计算得到的单晶体RDX 炸药的爆热值较其余两类更为准确。

5)此爆热值同样适用于各类混装炸药爆热的计算。