换个思路,让问题更简单
高睿喆

我很喜欢数学。在数学中,解决问题的过程是非常有挑战性和有意思的。我尤其喜欢几何图形问题。很多时候,我能盯着一个图形看好久,也不觉得厌烦。但是,最近有这样一道题目,让我有点不知所措。
如图1,在一个正方形中,以相邻两条边为直径,分别画半圆。求阴影部分的面积。
“这怎么求啊?阴影部分是不规则图形,不能直接求面积;空白部分也是不规则图形,不能用正方形的面积减去空白部分的面积来计算。”我没有一点思路。
“你怎么了?”爸爸见我愁眉苦脸的,便过来问我。
“这道问题,我解不出来,也没有思路。”
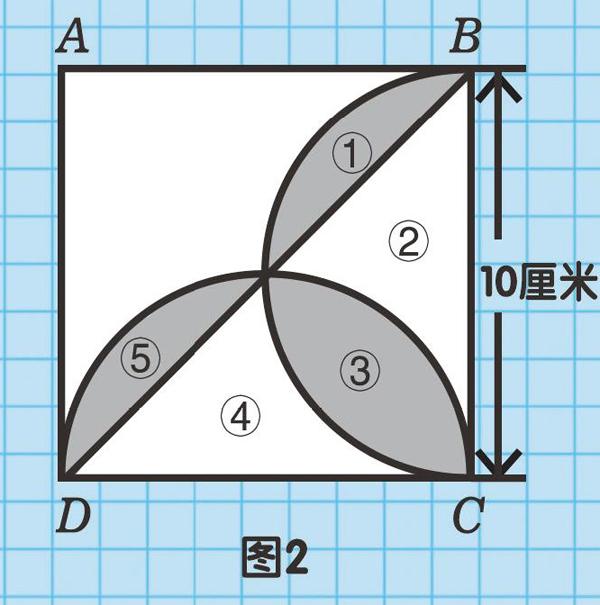
爸爸读了读题,并在图上标记了①②③④⑤(如图2)。询问了我的想法后,爸爸问:“这两个半圆有没有重叠的部分呀?”
“有呀,就是图形③的面积。”
“那你再看看,两个半圆的面积之和又是哪些部分呢?”爸爸接着问。
我想了想,试探性地回答道:“就是图形①②③④⑤的面积之和。”我又看了看爸爸,“不对,应该再加上一个图形③的面积。”
“对了,那你再看看图形②③④的面积之和是什么呀?”
根据爸爸的提示,我发现图形②③④的面积之和正好是直角三角形BCD的面积。瞬间,我恍然大悟,激动地喊道:“爸爸,我知道怎么做了!阴影部分的面积等于两个半圆的面积和,再减去直角三角形BCD的面积,也就是直径为10厘米的圆的面积,减去直角三角形BCD的面积。是吗?”
“是的,赶快记录下你的成果。”
直径为10厘米的圆的面积等于(10÷2)×(10÷2)π =25π (平方厘米),直角三角形BCD的面积等于 10×10×1
2=50(平方厘米),所以阴影部分的面积等于 25π-50=25(π-2)(平方厘米)。
“真棒,你真是位数学小达人!”听到爸爸夸我,我高兴极了!
爸爸接着说:“以后解决问题时,就要像今天一样,当你没有思路的時候,一定要仔细地观察,换一种思路思考问题,也许它会变得很简单!”
“以后在解决数学问题时,我一定要认真观察,努力去寻找更合适、更简便的解决方案。”我肯定地说。
我也相信此时的你和我一样,已经理解并学会了这种解题方法。
指导老师 李小强
杨咏琦 11月4日 14:14:20
思路打开了,难题就迎刃而解了。有时候将图形稍作变化,就能让题目变得简单。就像睿喆在爸爸的提示下,将不规则图形的面积,转化为多个规则图形面积的和或差,真是巧妙,我要鼓掌!
葛淑娜 11月4日 14:20:55
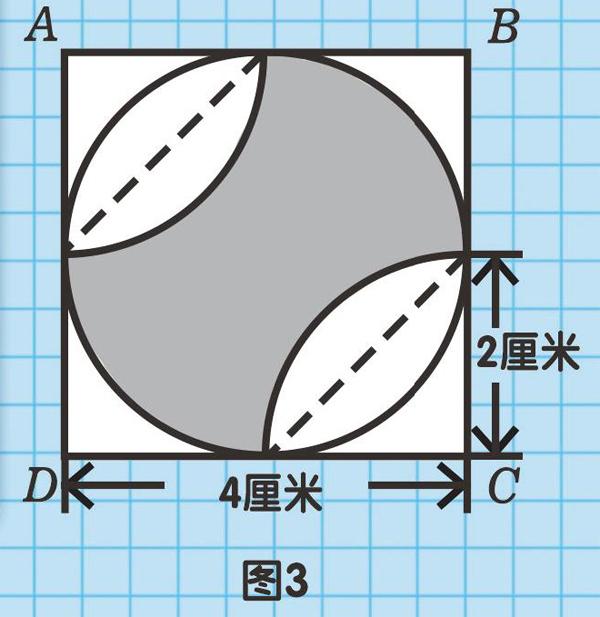
睿喆真的很棒,一点就通!我之前也遇到过类似的难题,现在想场外求助大家,请大家帮我解答一下这道困扰我许久的难题。如图3,以正方形ABCD的边长为直径画一个圆,阴影部分面积是多少呢?
高姣姣 11月4日 15:41:33
让我来!阴影部分的面积,是圆的面积减去圆中的两处空白部分的面积。有了!求出以2厘米为半径的圆的面积的四分之一,再减去一个等腰直角三角形的面积,得到的结果再乘以4,就是圆中空白部分的面积。那么阴影部分的面积为2×2π-(2×2π×1
4-2×2×1
2)×4=8(平方厘米)。

