强震下大跨度三心圆钢管拱桁架结构体系动力弹塑性失效分析

王敏 王俊刚

摘要：本文运用SAP2000结构分析软件，对某钢管拱桁架结构体系 （跨度58m，矢夸比0.38，三心圆）的整体结构模型进行了在EL-cenro地震作用下的弹塑性增量动力响应分析，研究中采用集中塑性铰理论考虑材料的非线性并同时计入结构的几何非线性影响。研究结果表明：该钢管拱桁架破坏过程中，材料塑性发展充分，属强度破坏，且承载力相对较高，抗震能力突出。

Abstract： This paper uses SAP2000 structural analysis software to analyze the elastoplastic incremental dynamic response of a steel tubular arch truss structure system （span 58m， sagitta than 0.38， three-hearted circle） under EL-cenro earthquake. In the study， the concentrated plastic hinge theory is used to consider the nonlinearity of the material and simultaneously account for the geometric nonlinear effects of the structure. The research results show that during the failure process of the steel tubular arch truss， the plasticity of the material is fully developed， which is a kind of strength damage， and the bearing capacity is relatively high， and the seismic resistance is outstanding.

关键词：强震;弹塑性时程分析;钢管拱桁架

Key words： strong earthquake;elastoplastic time history analysis;steel tube arch truss

中图分类号：TU27                                       文献标识码：A                                  文章编号：1006-4311（2019）30-0189-02

0  引言

近年来，大跨度结构建筑在抗震救灾工作中发挥了举足轻重的作用，常作为地震避难所和救灾指挥的场地使用。因此，对此类结构的设计提出了更高的要求，不仅要求进行多遇地震的设计验算，而且應对其在强烈地震下特别是超过规范设防烈度以后的地震烈度进行分析，以确保其在强震后可作为地震避难所使用[1]。为此研究该类结构强震下的弹塑性失效模态对其进行抗倒塌性能设计具有重要的防灾减灾意义。某钢管拱桁架结构体系 （跨度58m，矢夸比0.38，三心圆）的整体结构模型为研究对象，采用塑性铰理论和SAP2000分析软件对结构整体进行弹塑性时程分析，研究其在强震作用下的破坏形态、机理和极限承载力[2]。

1  结构设计

该结构拟采用三心圆钢管拱桁架结构体系，跨度58m，矢夸比0.38，厚度2.4m，三心圆半径分别为17m、34m、17m，圆心角分别为45°、90°、45°，上下弦均设置铰接支座，间距7.2m。结构布置如图1所示。

荷载标准值：①结构自重由程序自动计算;②屋面活荷载0.5kN/m2;活载值=max{屋面活荷载标准值，雪荷载标准值};③屋面板采用玻璃幕墙（8mm+12A+8mm），恒荷载为0.016×2560×10×1.3=0.53kN/m2;④基本风压0.4kN/m2。

抗震设防烈度为8度（0.20g，第一组），场地类别为Ⅲ类，特征周期值为0.45s，阻尼比弹性时取0.02，弹塑性时取0.05;结构设计基准期50年。

材料为Q235B级钢，弹性模量为205E03N/mm2，泊松比为0.3。

首先采用SAP2000按国家现行规范进行结构设计。所有杆件均按轴心受力构件进行设计，分析时采用杆单元。杆件应力比控制在1.0以内。设计杆件尺寸为：上弦杆？准127×4;下弦杆？准127×4;腹杆70×3。

2  动力弹塑性时程分析

2.1 初始条件

采用软件SAP2000，选用适合Ⅲ类场地的一组强震记录EL-Centro波，对结构进行动力弹塑性动力增量（IDA）时程分析，时长为19秒。计算分析时把恒载和0.5倍的雪载作用下的内力和变形状态作为动力弹塑性时程分析的初始条件。地震波的输入方向考虑X向和Z向的组合输入，其中最不利组合为：1.2恒载+1.4活荷载+1.3水平地震（X）+0.5竖向地震（Z）。

利用“屈服力和屈服位移”归一化法，定义铰的“广义力—广义位移”曲线，详细参见FEMA356。为了保证计算精度和计算效率，在上弦杆、下弦杆、腹杆的中间位置设置轴力铰。

2.2 EL-centro波作用下弹塑性动力响应分析

2.2.1 塑性发展与破坏形态

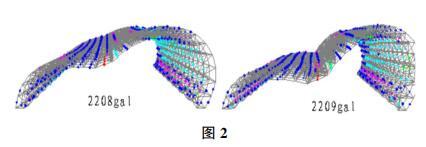
采用动力增量法对结构进行时程分析。地震作用效应组合为1.3水平+0.5竖向。当地震波加速度峰值较小时，结构变形为弹性小变形;当加速度峰值达到400gal时，结构开始进入弹塑性状态，在上弦靠近支座处出现第一批塑性铰;随着加速度峰值的增加，塑性铰的数量会逐渐增加;当加速度峰值达到2209时，结构响应处于发散状态，失效时的变形形态和塑性铰分布如图2所示，由图可见：上下弦杆塑性发展充分，腹杆大部分处在弹性阶段，且上弦杆拱脚处较跨中处破坏严重，下弦杆跨中处较拱脚处破坏严重，腹杆塑性铰集中在拱脚处。

2.2.2 动力失效分析

采用sap2000软件模拟结果如下。

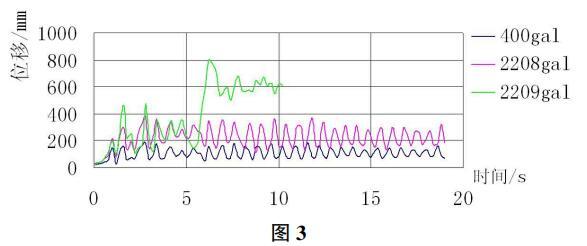
图3为最大位移节点的位移-加速度曲线，当地震作用较小时，杆件处于弹性阶段，刚度没有明显变化，随着地震作用的加大，大部分杆件进入弹塑性阶段，刚度也逐之减小，最终，位移发散，刚度降为零，结构失效。

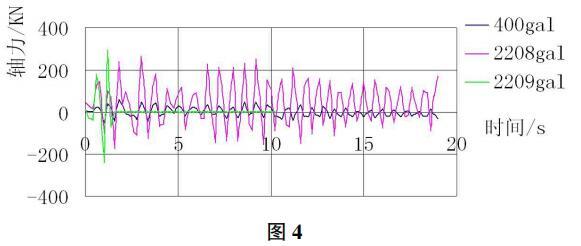
图4为最大杆件轴力时程曲线，杆件大部分时间处于受拉状态，当荷载超过其抗拉强度时，此杆首先发生强度破坏，从而引起其周围杆件内力重分布，近而导致这些杆件也发生强度破坏，造成结构局部刚度弱化，最终使得整体结构丧失稳定而倒塌。

综合考虑破坏过程中，结构的最大节点位移、进入塑性杆件比例逐渐增加，结构刚度逐渐弱化，此钢管拱桁架应属于局部强度破坏引起的整体失稳倒塌。

3  结论

①从结构失效时的塑性铰分布来看，大部分上弦杆和下弦杆可以进入塑性阶段，且上弦杆拱脚处较跨中部位的塑性铰发展程度充分，下弦杆跨中部位较拱脚处的塑性铰发展充分，然而腹杆只有拱脚处塑性铰较多，其余部位并没有进入塑性阶段。因此，建议在此类结构设计时，应注意对薄弱部位（上弦拱脚处，下弦跨中处，腹杆拱脚处）的设计。

②结合最大位移节点的位移-加速度曲线及最大杆件轴力时程曲线，可知，在强震作用下，结构破坏首先发生在下弦跨中处，且属于强度破坏，最终导致结构发生整体失稳而倒塌。

参考文献：

[1]李海旺.大跨鋼网格结构地震避难所抗震设计方法研究[D].太原：太原理工大学，2013.

[2]孙伟苹.强震下180m跨三心圆钢管空间拱桁架动力弹塑性分析[D].太原：太原理工大学，2012.

[3]黄初涛，王惠民，刘时宜，肖启仁，赵帅，姚激，张庆.某钢框架结构的弹塑性减震方案分析[J].价值工程，2018，37（01）：99-102.