基于结构反求的折线轴无试重动平衡方法
徐 远, 易 均, 邓 合, 周 帆, 韩志甲, 曾明浩
(中国工程物理研究院材料研究所,四川 江油 621907)
旋转机械在运行过程中经常会发生振动,大部分情况下,均是由于机器转子的质量不平衡引起的,约占所有引起原因的60%。在摇摆式气体循环增压泵(摇摆泵)研制过程中,其关键传动部件为一根折线轴,高速旋转时,惯性主轴偏离回转中心,产生较大的离心力,造成振动冲击。为保证泵组的使用寿命及压缩性能,需采用动平衡方法,通过配重改变折线轴的质量分布,减小不平衡量。ITER氚工厂中的Thales PR-130摇摆泵[1]结构示意如图1所示,8号、9号部件均为配重块。

图1 Thales PR-130摇摆泵Fig.1 Thales PR-130 wobble plate pump
根据转子的回转特性和力学特点,可分为刚性转子和挠性转子。对于刚性转子,运行中转子本身的弯曲可忽略不计,其不平衡量不随转速变化。而挠性转子离心力引起的弯曲变形不能直接忽略,变形量会改变转子的质量分布,进而改变转子的不平衡状态。对摇摆泵的折线轴进行模态分析:一阶固有频率为972.7 Hz,一阶临界转速约58 000 r/min,远高于正常工作时的最高转速2 000 r/min。因此,在折线轴的动平衡中,可将其视为刚性转子进行动力学分析(见图2)。

图2 折线轴一阶模态振型Fig.2 The first model shape of folding shaft
对于刚性转子,目前的动平衡方法大致可以分为两种思路。一种是在转子上加试重,使试重所产生的离心力和转子系统原有不平衡量所产生的离心力相互抵消,如目前广泛应用的动平衡机测试和有限元仿真。动平衡机一般采用基于影响系数法的双面动平衡原理,通过对转子加试重,测得试重对转子不平衡响应的影响,计算出应加的平衡配重[2]。有限元仿真则利用有限元分析方法,建立出动平衡机的有限元模型,通过在模型上添加试重,进而求解出不平衡转子应加的平衡配重[3-6]。
另一方面,找出不平衡量的大小和方位,在对应的位置消除不平衡量,将初始不平衡量所产生的影响降低至最小,即无试重动平衡。如在理论上预先设计出动平衡性能极佳的转子模型,节约转子的设计开发成本。早期转子动平衡的理论计算主要依靠数学解析法,计算量浩大,计算精度也不高。随着计算机的普及和各种软件的应用,为转子动平衡的设计、计算提供了很好的平台,提高了转子的终平衡效果。章云等[7-8]通过扩展影响系数动平衡方法与转子动力学模型的比较分析,得出了动力学传递函数与影响系数之间的关联关系,求解出了等效集中和分布式的不平衡量,有效地降低了转子旋转时的振动幅值。Kang等[9]使用UG建模对发动机曲轴模锻件进行有限次等距离分割,并根据转子双面动平衡原理对数据文件进行编译以获得曲轴的不平衡量。Van Der Wijk等[10]分析了两缸曲轴的平衡方法,在CAD软件的辅助下,采用线性方程求解曲轴的不平衡量。
虽然上述方法都能求解出转子的不平衡量,但其算法共同点均是采用垂直于回转轴线的截面作为校正面。由于摇摆泵的功能需求,折线轴不能设计为对称结构。若使用现有方法进行折线轴的动平衡,唯有限定住斜轴处配重块的质心偏移距离R2,求解结果才能真正用于动平衡。在图3所示的折线轴斜轴配重示意图中,选定斜轴处的配重位置,使用现有方法只能求解出垂直于回转轴线的校正面上的不平衡量U2。由于实际配重截面垂直于惯性主轴,配重块的质心M2必须刚好位于实际配重截面、校正面和折线轴对称面的交点处,对应唯一的动平衡方案。但是,在摇摆泵的研制过程中,折线轴的动平衡需综合考虑最终平衡效果和实际安装空间限制,唯一特定的M2和R2解不一定能够设计出符合实际应用需求的配重块。此外,若采用动平衡机进行配重试验,由于折线轴安装在摇摆泵的内部,每次平衡块的调整都意味着重复组装,重新选定校正面,再进行不平衡量的计算,费时费力。因此,急需一种专门用于折线轴的多方案快速平衡的无试重动平衡方法。
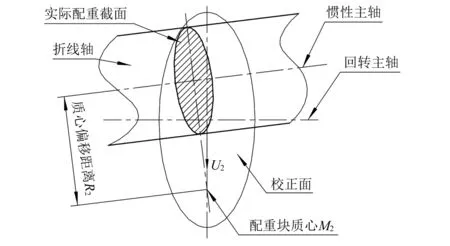
图3 折线轴斜轴配重示意图Fig.3 Counter-weight of oblique-axis
1 动平衡状态参数模型
1.1 折线轴不平衡量
旋转机械在匀速运转时,内部的每个质点都会产生相应的惯性力,组成惯性力系。根据刚体力学原理,该惯性力系可简化成一个主矢R和主矩M。当R=0,M=0时,刚性转子达到动平衡。
采用无试重方法对刚性转子进行动平衡,首先需确定转子的不平衡量。对于传统的铸锻件,制造误差影响较大,无法通过几何测量和三维扫描等手段精确复现出转子的具体模型,只能通过测量由转子和动平衡机组成的转子-支撑系统中的支撑动反力确定校正面上的不平衡量。折线轴采用高精度车、铣方式加工,表面质量好,采用三坐标机进行几何尺寸的测量,通过建模软件可以精确建立出转子的三维模型,并确定转子的质心位置。但是,由于折线轴并非两端支撑类型,建模软件只能确定转子的静不平衡量。折线轴旋转时,斜轴部分弯矩所引起的不平衡力不能忽略。因此,采用仿真软件根据折线轴的三维模型建立起轴承支撑模型,测量折线轴旋转时引起的轴承支撑反力,即可确定折线轴旋转时的不平衡量。
在图4所示的折线轴支撑示意图中,忽略掉折线轴的制造误差,每处质量相对于YOZ平面对称分布。折线轴达到动平衡的充要条件为

(1)
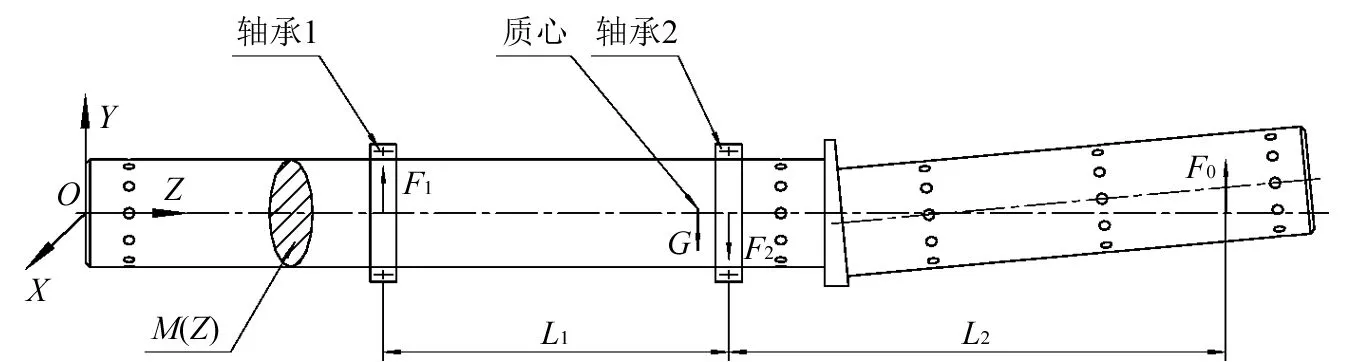
图4 折线轴支撑示意图Fig.4 The supporting diagram of folding shaft
对折线轴进行分析,其惯性主轴与旋转主轴在质心G以外的点相交,属于准静不平衡状态,不平衡量在效果上可等效于一个静不平衡量与一个力偶不平衡量之和,可在一个校正面上加减配重进行平衡[11]。采用ADAMS建立折线轴动力学模型,仿真折线轴在轴承支撑情况下的运动状态,得到匀速运转时两边轴承的支撑反力变化规律,如图5所示,两边轴承所受到的惯性力相位相差180°。
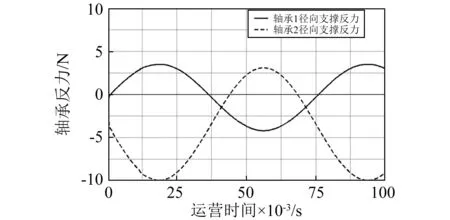
图5 折线轴未平衡时轴承径向支撑反力变化图 (n=800 r/min)Fig.5 The change of bearing radial support reaction when the folding shaft out-off-balance(n=800 r/min)
(2)

轴承支撑反力的恒定部分为折线轴重量G的分量,随时间变化部分则由旋转时的惯性力引起,即不平衡量。通过力学分析,可将该不平衡量等效成作用于折线轴对称面上的一恒力F0,如图6所示。通过在F0作用面反向加载平衡配重,即可实现动平衡。
(3)

图6 折线轴实际配重位置图Fig.6 The actual counter-weight of folding shaft
1.2 折线轴动平衡状态参数模型
基于摇摆泵的特殊结构,不能在F0作用截面进行配重,只能在两端指定的截面上进行配重。通过力学计算,可将F0分解到两端的实际配重截面上,只需在这两个截面上进行配重,即可使折线轴达到动平衡。在图6所示的折线轴实际配重位置图中,直轴配重截面垂直于回转主轴,斜轴配重截面垂直于惯性主轴,折线轴达到动平衡的充要条件为
(4)
式中:M1,M2分别为配重块1和2的质量;R1,R2分别为配重块1和2的质心偏移折线轴惯性主轴线的距离;ω为折线轴旋转的角速度;其余折线轴尺寸参数如图6所示。
简化后,即可得到折线轴的动平衡状态参数模型
(5)
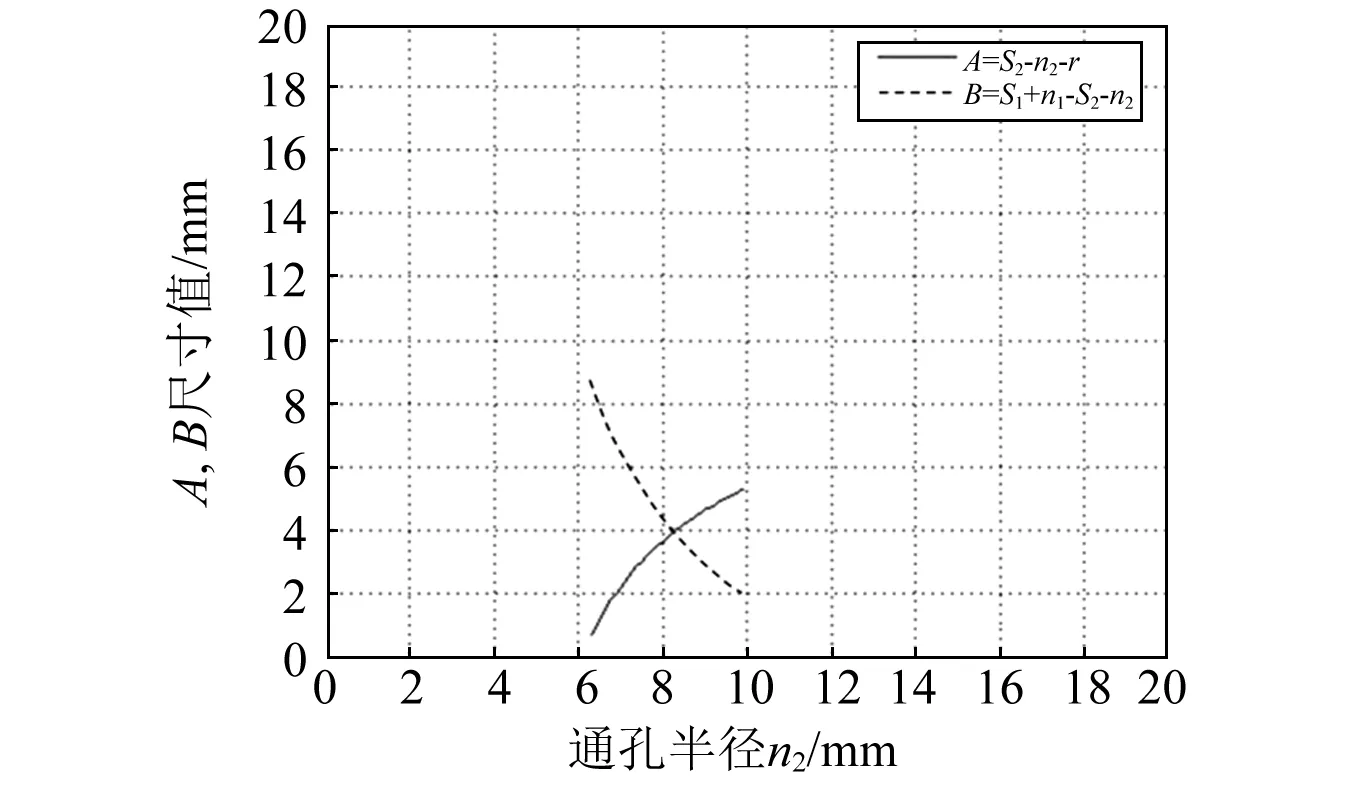
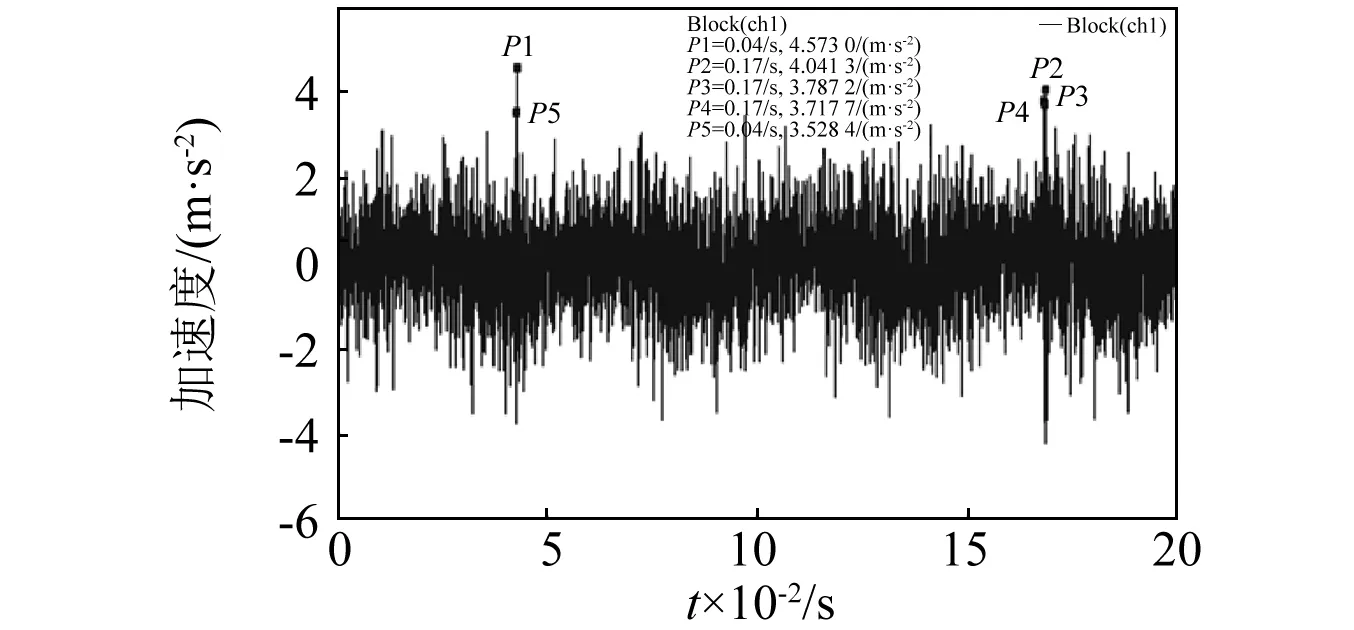
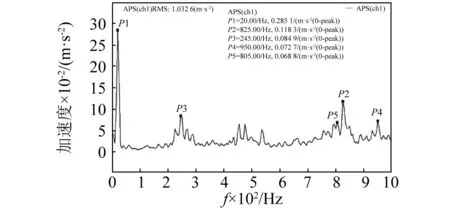
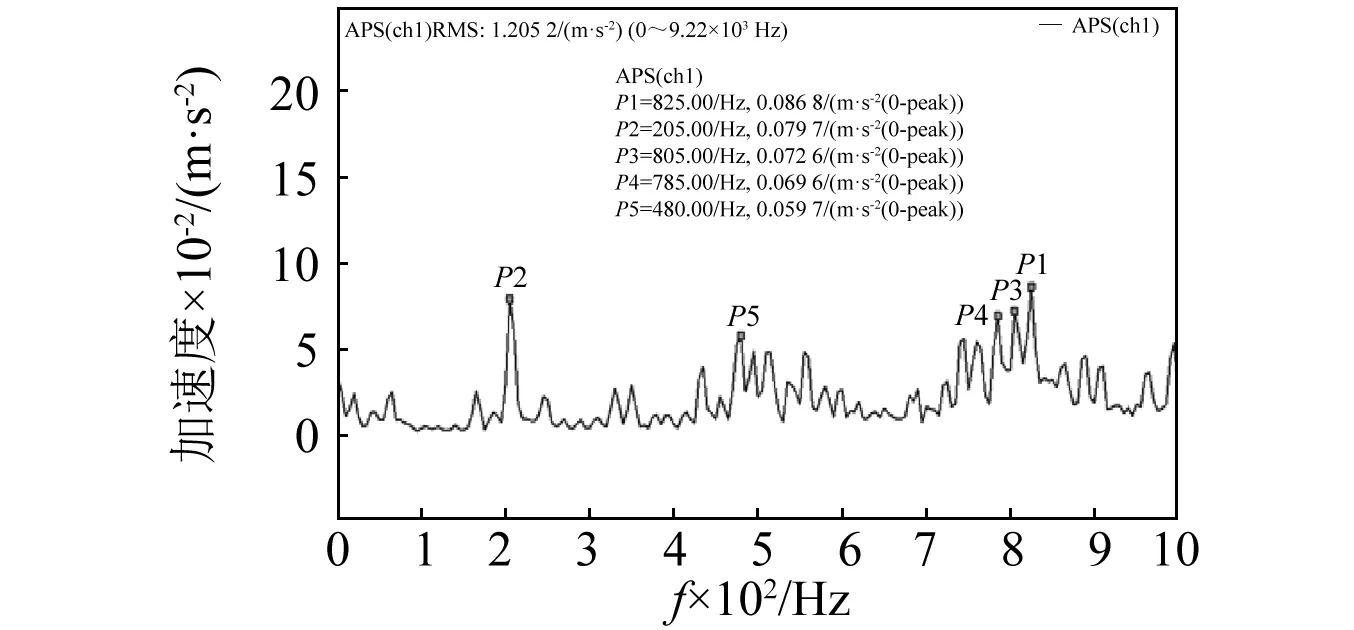
未知参数为直轴配重块1的质径积M1R1,斜轴配重块2的质量M2和质心偏移距离R2,结果为一空间解集,如图7所示。在模型中添加摇摆泵的结构限制条件5 图7 动平衡状态模型空间解集Fig.7 The solution space of parameter model 图8 折线轴动平衡解集Fig.8 The solution space of folding shaft when balancing 根据折线轴的动平衡状态参数模型,可以获得多种配重方案,每种方案对应一组配重块特征值:直轴配重块1的质径积M1R1、斜轴配重块2的质量M2和质心偏移距离R2。在实际应用时,设计的配重块需满足相应的特征值要求。因此,需根据已知的特征值,进行配重块的反求设计。 司中柱[12]在静力学模型的基础上,以零件固有频率和固有振型为约束条件,通过修改各个节点的质量来获得满足需求的动力学模型。应用该方法,可以在各向异性的材料中通过改变质量分布获得满足质量和质心要求的零件。但在工程应用时,大部分无明显内部缺陷的材料,其质量均匀分布,微弱的材料各项异性对质量和质心位置影响较小,结构尺寸才是影响质量和质心位置的关键因素。因此,在折线轴的配重块设计时,忽略材料的各向异性。对于各向同性的材料,其质心计算公式为 (6) 为缩短开发时间,减少未知参数的求解,配重块尽量设计为对称结构。在配重块1的结构设计中,其目标特征值为质径积M1R1。根据摇摆泵的实际安装空间及折线轴结构,设计了如图9所示的配重块1,结构在纵向和厚度方向对称分布,材质为304不锈钢,厚度为h,密度为ρ,两半圆的圆心距离S为未知参数。根据质心计算公式,配重块的质径积等于各部分质径积之和,即 (7) (8) 式中:m1,m2,m3分别为配重块1在图9中所示1、2、3部分的质量;l1,l2,l3为各部分质心偏移安装通孔r1中心线的距离。 图9 配重块1示意图Fig.9 The sketch map of balance weight 1 将配重块1的质径积M1R1代入式(8)中,即可求解配重块1的未知尺寸S,设计出符合目标特征值的配重块。 将上述方法进行拓展,对斜轴配重块2进行反求设计。配重块2需满足特定的质量M2和质心偏移距离R2要求。经过多次建模求解发现,当配重块2的结构设计成2个或3个未知参数时,减重孔会超出实体尺寸,无法进行制造。当未知尺寸的个数大于等于4时,才有合适的解集。为减小计算量,尺寸未知参数选定为4个。配重块2在纵向和厚度方向上对称分布:材质为304不锈钢;厚度为h;密度为ρ;两半圆的圆心距离为S1;两通孔间的中心距为S2;配重块2外形半径为n1;减重孔半径为n2;S1,S2,n1,n2均为未知参数,如图10所示。 图10 配重块2示意图Fig.10 The sketch map of balance weight 2 配重块2需满足质量M2和质心偏移距离R2要求 (9) 即 (10) 对于该四元方程组,结果为一空间解集。根据摇摆泵的结构需求,在该方程组的基础上,添加上配重块2的尺寸限制条件,如外径n1大于通孔外径r,减重孔需在配重块2的外形范围内,减重孔不得与通孔相交等,进一步缩小解集范围。 n1>r,2n1={1,2,3…+∞}S1+n1>S2+n2S2>r+n2n2>n1 采用Matlab对上述方程组与限制条件进行数学建模。对每一组M2和R2,n1对应有限个数值使得方程组有解。如取M1R1=0.017 8 kg·mm,则M2=0.096 8 kg,R2=0.824 mm,对应n1的解集有{18,18.5,19,19.5},对每一个n1进行分析,未知参数S1,S2,n2的空间解集如图11所示。 图11 配重块2未知参数空间解集(n1=18 mm)Fig.11 The solution space of balance weight 2(n1=18 mm) 在n1的有限个解中,任选其一均可设计出满足要求的配重块2。根据结构设计相关原则,零件质量均匀分布,各尺寸相对称,应力均匀分布。对于特定的n1,分析减重孔半径n2的变化对两侧剩余实体尺寸A,B的影响,A,B位置如图10所示。当n1=18 mm时,实体尺寸A,B随减重孔半径n2的变化规律如图12所示。为使两边实体均匀分布,n2选取曲线接近交点位置的数值,即n2=8 mm,将n1,n2的数值代入式(10)中,即可求解出S1,S2的尺寸值,并设计出对应的配重块2。至此,就完成了与动平衡解集相对应的配重块的设计。 图12 尺寸A,B变化规律(n1=18 mm)Fig.12 The variation trend of A and B(n1=18 mm) 为了判断上述无试重动平衡方法的有效性,建立了轴承支撑模型对折线轴的运行状态进行仿真,测量轴承在径向方向的支撑反力,量化折线轴配重后的残余不平衡量。根据上述无试重动平衡方法所获得的动平衡解集,分别选取了M1R1为0.017 8 kg·mm,0.018 2 kg·mm,0.018 6 kg·mm,0.018 8 kg·mm四种动平衡方案,设计出了相应的配重块,进行仿真验证,得到轴承在X方向的径向支撑反力如图13所示,平衡效果对比如表1所示。 此外,随着配重块1质径积M1R1的增大,配重块2的质量M2呈指数型减小,质心偏移距离R2呈线性增大,动平衡效果愈好,如图14和图15所示。从仿真结果中可以看出,采用上述无试重动平衡方法,除了对轴承造成恒定的作用力外,均从不同程度上减小了折线轴的残余不平衡量,使轴承支撑反力的波动幅度大幅减小。当M1R1=0.017 8 kg·mm时,波动幅度减小至10%;当M1R1=0.018 8 kg·mm时,波动幅度减小至3.0%。 图13 轴承X方向的径向支撑反力Fig.13 The change of bearing radial support reaction in X direction 动平衡方案轴承1支撑反力/N轴承2支撑反力/N残余不平衡量/%无配重F→1=-0.336+3.845sin(ωt)F→2=-3.426+6.517sin(ωt+180°)M1R1=0.017 8 kg·mmM2=93.9 g,R2=8.5 mmF→1=0.754+0.402sin(ωt)F→2=-5.671+0.595sin(ωt+180°)10.5M1R1=0.018 2 kg·mmM2=50.6 g,R2=14.3 mmF→1=0.077+0.216sin(ωt)F→2=-4.561+0.354sin(ωt+180°)5.6M1R1=0.018 6 kg·mmM2=34.2 g,R2=17.6 mmF→1=-0.180+0.125sin(ωt)F→2=-3.929+0.211sin(ωt+180°)3.2M1R1=0.018 8 kg·mmM2=31.1 g,R2=18.7 mmF→1=-0.226+0.111sin(ωt)F→2=-3.991+0.198sin(ωt+180°)3.0 图14 配重块2质量M2变化规律Fig.14 The quality variation trend of balance weight 2 图15 配重块2质心偏移距离R2变化规律Fig.15 The centroid distance variation trend of balance weight 2 按照上述四种动平衡方案所设计出的配重块尺寸,加工出了配重块实物,利用动平衡机为支撑平台,CoCo-90为数据采集设备,对折线轴前轴承处的径向振动加速度进行了测量。折线轴未加配重时的振动加速度采集数据块如图16所示,实验转速为1 200 r/min。 图16 未加配重时的振动加速度Fig.16 Vibration acceleration of no counterweight 添加上配重块后,测量折线轴旋转时的振动加速度。四种动平衡方案所对应的振动加速度虽然均有不同程度的减小,但减小幅度并不大。另外,由于外界信号的干扰,振动加速度幅值具有一定的随机性,不能用其衡量折线轴的残余不平衡量。为准确表征折线轴不平衡量所引入的振动能量,对振动加速度信号进行了频谱分析,得到其自功率谱,如图17~图21所示。 图17 振动加速度自功率谱(无配重)Fig.17 Auto-power spectrum of vibration acceleration (no counterweight) 图18 振动加速度自功率谱(M1R1=0.017 8)Fig.18 Auto-power spectrum of vibration acceleration (M1R1=0.017 8) 图19 振动加速度自功率谱(M1R1=0.018 2)Fig.19 Auto-power spectrum of vibration acceleration (M1R1=0.018 2) 图20 振动加速度自功率谱(M1R1=0.018 6)Fig.20 Auto-power spectrum of vibration acceleration (M1R1=0.018 6) 图21 振动加速度自功率谱(M1R1=0.018 8)Fig.21 Auto-power spectrum of vibration acceleration (M1R1=0.018 8) 未加配重块时,所测振动加速度信号的自功率谱峰值在20 Hz左右,大小为0.285 1 m/s2。添加上配重块后,基频处的自功率谱幅值大幅减小,自功率谱峰值出现在中高频处,因折线轴不平衡量引起的振动能量大幅减小,振动加速度的影响源转换为电机、轴承、支撑平台等环境因素,折线轴基本实现了动平衡。实验数据对比如表2所示。 实验结果表明,由于支撑平台及轴承等环境因素的影响,虽然各平衡方案所对应的振动加速度并没有明显减小,但各信号所对应的自功率谱峰值及基频幅值相对无配重块时均大幅减小,四种方案所对应的残余不平衡量减小趋势也与仿真结果相吻合,微小数据差异主要来源于配重块的制造、装配误差和测量误差。因此,该无试重动平衡方法所求解出的所有动平衡方案均可减小折线轴旋转时的不平衡量,配重块的结构反求设计方法行之有效。另外,将该无试重动平衡方法进行拓展,考虑其他弹性单元及气体压缩后的反力,可用于折线轴装配后的摇摆泵整体动平衡。 表2 实验数据对比Tab.2 Contrasts of the experimental data 在摇摆泵研制过程中,为了满足折线轴无试重及多方案快速动平衡的需求,通过建立基于配重块特征值的动平衡状态参数模型及多元参数化结构反求设计方法,形成了适用于折线轴的无试重动平衡方法。通过该方法,不仅有效地降低了折线轴旋转时的不平衡量,还可以提供多种动平衡方案以便摇摆泵的迭代设计,为泵组的整体动平衡提供了新方法,也对通过零件特征值进行结构尺寸的反求设计提供了新思路。

2 参数化结构反求
2.1 一元参数化结构反求

2.2 四元参数化结构反求

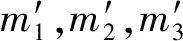
3 动平衡方案验证
3.1 仿真验证




3.2 动平衡实验验证




4 结 论

