舰船地震波远程定位方法研究

薛泽利，张晓峻,侯金弟，孙晶华

(1.佳木斯大学 理学院，黑龙江 佳木斯 154007；2.哈尔滨工程大学 物理与光电工程学院，黑龙江 哈尔滨 150001)

随着舰船制造技术的提高，水声高频信号被进一步抑制，传统水听器由于尺寸、设计原理等原因很难准确有效检测低频信号[1]. 同时浅海海域的地形复杂，浑浊海水对声波的吸收，不利于水声的远程传播[2]，因此利用水声远程定位舰船目标变得越来越困难. 在浅海海域舰船水声传播至海底沉积层表面形成了足够能量的舰船地震波，可以远程传播[3]，因此利用舰船地震波远程定位，可以弥补水声远程定位的不足.

舰船地震波是水声在海底沉积层表面形成的椭圆波，舰船地震波能量主要集中在固体-液体分界表面[4]，沿着固体-液体分界面上衰减缓慢，可以远程传播. 海底地震计组成的九元环形阵列具有波数响应灵敏度高、各方向响应均匀等优点. 基于此阵列，侧向定位和时差法无法准确定舰船目标，采用梯度下降算法和单纯形算法可以减小定位误差，实现稳定精确定位舰船目标.

1 舰船地震波耦合与传输

水声是一种纵波，当淤泥层的水声传播至沉积层表面与海底沉积层发生作用，使得沉积层发生应变. 其中切应变产生水平方向的振动变成纵波，正应变产生竖直方向的振动变成横波，所以纵波在沉积层表面作用点处发生波形转换. 水声在分界面处波形转换如图1所示，其中P波为纵波，S波为横波.

图1 水声在沉积层表面的波形转换

在沉积层作用点处，产生的S波又可以分解为振动方向垂直于分界面的SV波和平行于分界面的SH波[5]，舰船地震波是P波和SV波在淤泥层和沉积层分界表面合成的一种振动轨迹为沿着逆时针旋转的椭圆波，在图2所示的坐标系中，波的水平传播方向为x轴，垂直传播方向为z轴.

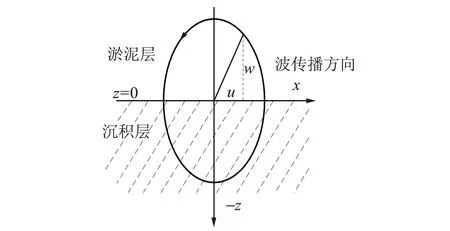
图2 舰船地震波位移

舰船地震波振动的位移分解为水平方向u和竖直方向w的位移[6]可以表示为

(1)

(2)

式(1)和式(2)中,λST为舰船地震波波长，vST为舰船地震波波速，ω为舰船地震波角速度，在式(2)和式(3)中的其他函数为

(3)

(4)

(5)

(6)

(7)

vP为纵波波速，vS为横波波速，舰船地震波满足于椭圆轨迹方程,

(8)

(9)

(10)

2 定位阵列

利用三维高灵敏度海底地震计可以检测舰船地震波[9]，但是利用单一海底地震计并不能实现对目标的定位，需要多个海底地震计组成的阵列才能实现对目标的定位. 如图3所示，建立九元海底地震计环形阵列，其中M0～M8表示海底地震计的位置，M0位于原点处，其他阵元M1～M8均匀地分布在圆周上，R为九元海底地震计环形阵列的半径.

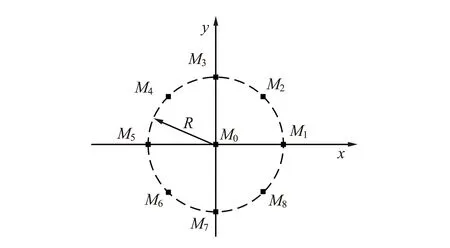
图3 九元环形阵

阵列的波数响应是阵列的重要指标，阵列的波数响应主瓣大而尖，并且边瓣小，表征阵列可以压制潜在的干扰信号，从而保证定位的精度. 阵列的波数响应[10]可以表示为

(11)

式中，N是海底地震计的数目，rj和rs表示海底地震计的位置矢量，九元海底地震计环形阵列半径R为1 km，波数响应图如图4所示，其中y(k)表示y方向的波数，x(k)表示x方向的波数，H(k)表示波数振幅响应.

(a)二维波数响应

(b)三维波数响应图4 九元圆形海底地震计阵列的波数响应

图4(a)中二维波数响应图表明，环形阵对每个方向的波数响应一致，也就是对每个方向的定位精度一致. 图4(b)中三维波数响应图表明，九元海底地震计环形阵列的波数响应主瓣高边瓣小，波数分辨率高，可以压制潜在的干扰信号，保证阵列定位的精度.

3 定位算法

利用海底地震计组成的阵列对舰船目标进行定位，最常用的定位方法是测向法定位和时差法定位[11]，但是利用测向法定位需要海底地震计能够准确地检测到舰船地震波的波达角. 当舰船目标在较远的位置移动时，舰船地震波的波达角变化很小，海底地震计难以准确检测到舰船地震波的方向. 时差法是利用海底地震计阵列检测舰船地震波到达不同海底地震计所形成的时间实现对目标的定位[12]. 时差法在求解目标位置时，通常不能得到唯一解，所以时差法通常不能得到目标的唯一坐标位置[13]. 针对侧向法和时差法的不足，采用梯度下降算法和单纯形算法对目标进行定位研究.

3.1 梯度下降算法

梯度下降算法是基于泰勒级数展开的算法[14]. 利用梯度下降算法对舰船目标定位，其运算的流程如图5所示，首先在二维坐标平面选取初始的点x0，计算初始点函数值，如果函数值f(x0)满足停止条件，停止运算输出结果x0，否则按照一定规则变换到下一个xk+1点继续运算，直到满足停止条件ε0，停止运算输出结果.

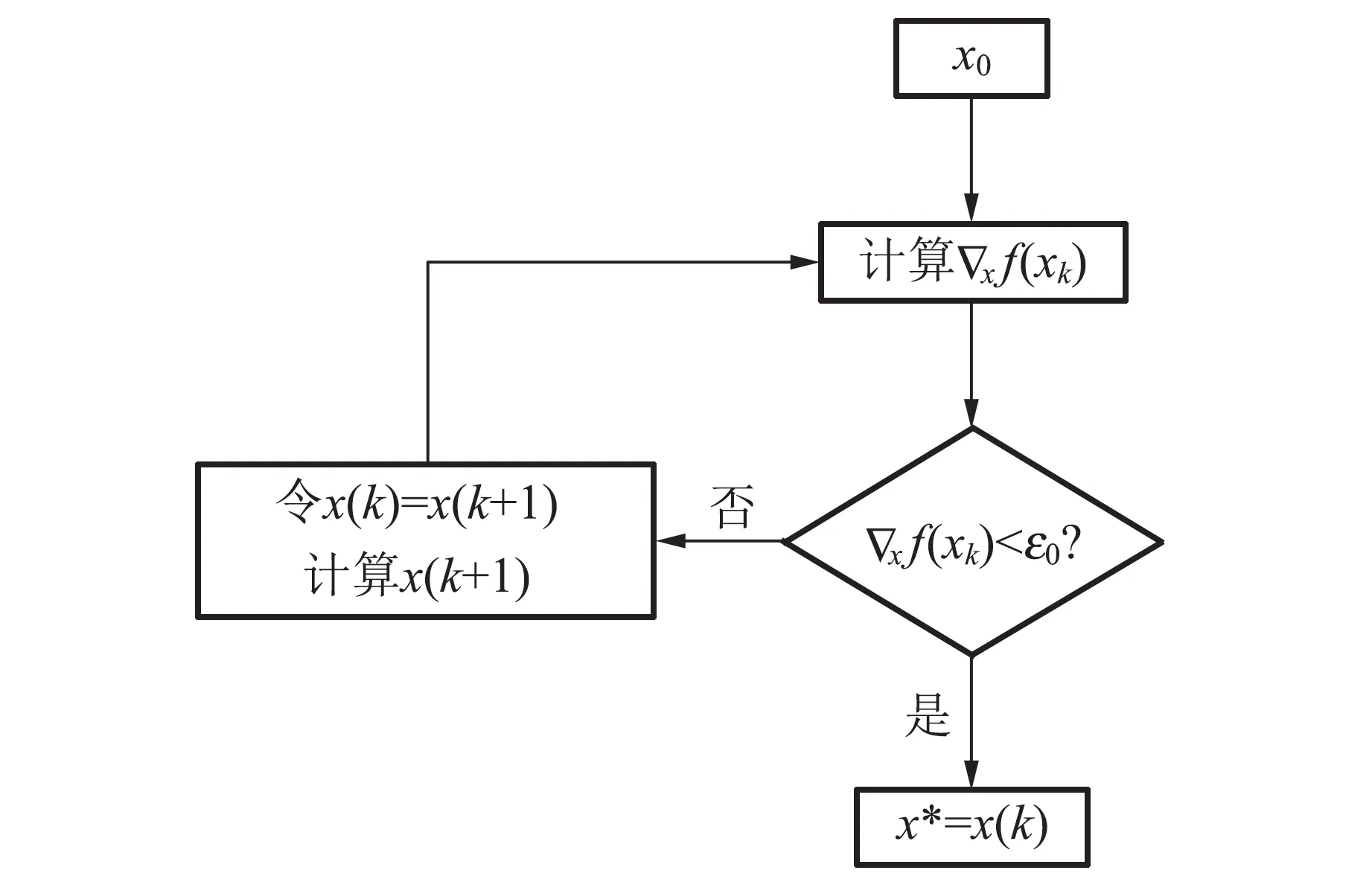
图5 梯度下降算法运算流程

依据时差法的定位原理，误差矢量可以表示为[15-16]

e(x)=Ax-(M-vSTτi‖x‖),

(12)

代价函数可以表示为

f(x)=eTe,

(13)

代价函数的梯度可以表示为

(14)

由第k个点变换到第k+1个点的变换准则为

x(k+1)=x(k)-μxf(xk),

(15)

其中中μ为下降速度.

3.2 单纯形算法

利用单纯形算法阵列定位的残差[17]可以表示为

(16)

式(16)中n为方程数，对于九元海底地震计环形阵列的方程数为8，对于二维平面定位q为3.ti为舰船地震波到达第i个传感器的时间，tm表示ti的中位数，在九元环形阵中tm=t0.

(17)

f(x)=E(x).

(18)

二维空间内的单纯形算法首先在二维空间定义3个任意点，分别为x1,x2和x3，3个点相互连接构成了“单纯形”. 定义一个函数为f(xi)，这个函数是误差函数，在这个二维空间的单纯性的各个顶点的函数值定义为

fi=f(xi),i=1,2,3.

(19)

在这个单纯形中，顶点的最大值和最小值分别定义为

fm=maxf(xi),

(20)

fn=minf(xi).

(21)

最大值顶点定义为xm，最小值顶点为xn，大于最小值且小于最大值的点定义为xg，单纯形的形心点[18]的坐标为

(22)

(23)

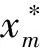
(24)

在式(24)中扩展系数V>1，形成新的单纯形，直到满足条件输出结果.

(25)

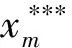
(26)

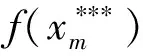
(27)

单纯形法算法运算流程图如图6所示[19].

图6 单纯形算法流程图

这种变化是把单纯形的边缩短了，紧缩系数为L=0.5，其中xi≠xm，形成新的单纯形继续循环，直到f(x*)的值满足设定的条件时停止运算. 单纯形算法每1次循环都是通过映射、扩展、压缩、缩短边长中的某一种方式变换得到新的单纯形[20]. 当单纯形的最大值满足设定的条件f(xm)<ε0时，停止运算输出xm，运算结束.

4 仿真计算

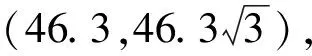
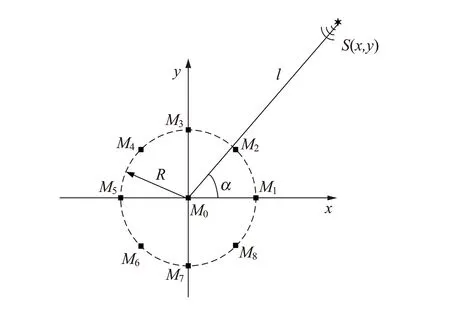
图7 九元海底地震计环形阵定位模型

利用梯度下降算法进行定位时首先选择初始点，通过初始点的变换，最终变换到估计的位置，研究初始点对定位的影响，选择3种不同初始点进行定位，初始点a的坐标位置为(2，2.5)，初始点b的坐标位置为(35，75)，初始点c的坐标位置为(40，25).

梯度下降算法3种不同的初始点定位的结果如表1所示，其中μ是下降速度设置为0.01，下降速度是进行运算时变换的步长，ε0是停止条件设置为0.001，当代价函数的梯度小于停止条件ε0时停止运算，输出估计的目标的位置S*. 其中利用a初始点最终估计的位置为(32.405，75.421)，其中利用b初始点最终估计的位置为(45.692，79.051)，其中利用c初始点最终估计的位置为(44.950，80.523).

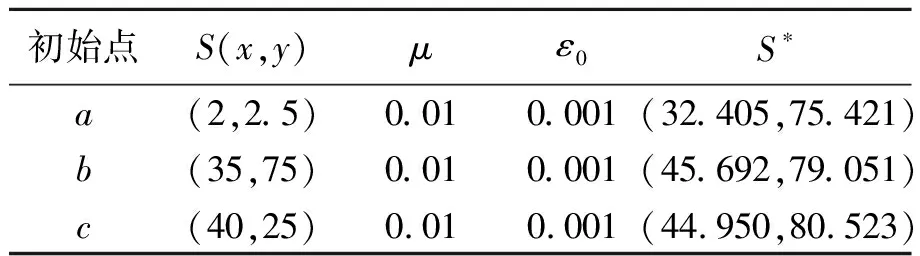
表1 梯度下降算法定位结果

研究初始单纯形对定位的影响，首先选择3种不同的初始单纯形进行定位，a初始单纯形的3个初始点分别为x1(1，2.5),x2(10，8.7),x3(6，50)，b初始单纯形的3个初始点分别为x1(30，45),x2(50，115),x3(65，50)，c初始单纯形的3个初始点分别为x1(50，10),x2(35，25),x3(65，40).

3种不同初始单纯形算法的定位结果如表2所示，其中T是映射系数设置为1，V是扩展系数设置为1.2，Z是压缩系数设置0.5，L是紧缩系数设置为0.5，ε0是停止条件设置为0.001，当阵列的残差小于停止条件时输出估计的目标的位置S*，最终a初始单纯形最大值点变换到(46.462，80.454)停止运算输出结果S*(46.462，80.454)，最终b初始单纯形最大值点变换到(46.418，80.351)停止运算输出结果S*(46.418，80.351)，c初始单纯形最大值点变换到(46.421，80.349)停止运算输出结果S*(46.421，80.349).

表2 单纯形算法定位结果

采用定位误差和对初始值的依赖程度对梯度下降算法和单纯形算法定位效果进行评价. 目标的定位误差是指算法估计的位置与实际位置的空间距离，定位误差可以表示为

(28)

(29)

在式(29)中，n表示定位的次数为3.

2种算法的定位误差和对初始值的依赖程度如表3所示，单纯形算法定位目标的误差约为0.2 km，对初始值的依赖程度为1.1×10-5km2. 与梯度下降算法相比，定位误差小，定位精度高，对初始值的依赖程度小，定位更加稳定，所以相比于梯度下降算法单纯形算法对目标定位优势更明显，更适合对舰船目标定位.

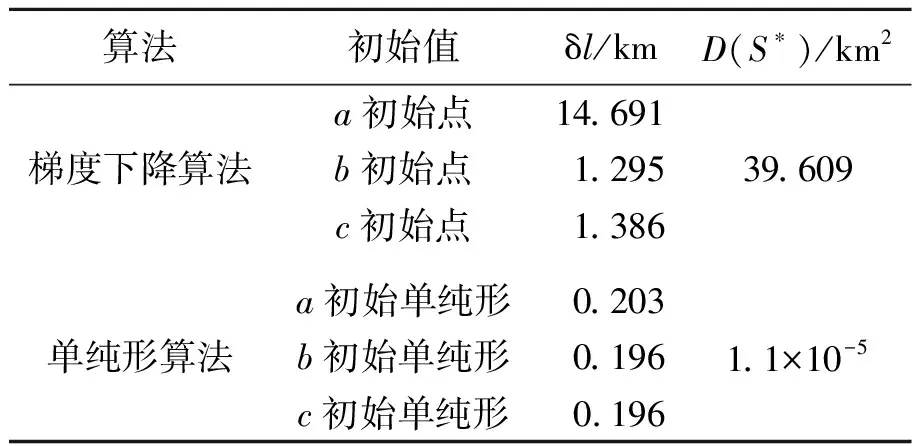
表3 算法定位性能

5 结 论

从理论上分析了舰船地震波形成的机理，固-液分界表面耦合特性及海底远程传播的特性，结果表明舰船地震波远程传输衰减小. 基于九元海底地震计环形阵列,研究了梯度下降算法和单纯形算法，结果表明：九元海底地震计环形阵列具有波数响应灵敏度高，各方向响应均匀的特点；利用梯度下降算法和单纯形算法对目标位置进行估计，可减小定位误差；单纯形算法定位误差更小，对初始值的依赖程度更小，定位更加稳定. 因此，基于舰船地震波实现远程目标定位具有可行性.