基于偏最小二乘法的翼型稳健设计替代模型

(西南科技大学 计算机科学与技术学院，四川 绵阳 621010)

0 引言

近几十来世界航空航天技术取得了迅猛的发展，航空航天已成为大国间的主要竞技场之一，也是国家综合实力的体现，而飞行器的设计又是航空航天的重要研发领域。机翼的设计是整个飞行器设计的核心之一，而翼型又是机翼设计的核心。如何快速、低成本地获得一个性能高效且稳定的翼型成为了研究人员关注的重点之一。

翼型的传统设计方法主要是通过风洞对研究人员建立的不同机翼模型进行试验，通过试验数据分析来选择最佳翼型，该种方法存在成本高、试验周期长等缺点。此外传统翼型设计中，设计人员在借鉴其过去设计经验时，可能会引起单点设计问题如对单一点马赫数处的阻力进行了优化设计，但引发了该点临域马赫数处的阻力出现剧烈波动的情况。在超声速翼型的设计中单点设计带来的性能波动会更加剧烈，在Hicks和Johnson的研究[1]中对单点设计问题进行了详细介绍。

在之后的研究中，研究人员们将计算流体动力学(Computational Fluid Dynamics，CFD)等相关数值计算用于翼型稳健设计。虽然通过CFD软件进行气动性能计算能降低传统风洞试验的成本，但是其计算时间仍然非常漫长。而通过将替代模型与CFD计算相结合的方法来进行翼型稳健设计，能够在保证精度需求的情况下大大缩减计算时间，能在基准翼型的基础上获得一个性能更优的稳健翼型。

1 翼型稳健设计及其目标模型

翼型的稳健设计就是要对选定的基准翼型进行优化，以最终获得一个对环境因素变化不敏感的稳健翼型。因此在翼型设计的初始阶段就要明确稳健设计针对的噪声因素，通过稳健设计方法来获取一组可控因素的最佳组合，从而实现稳健翼型对噪声因素不敏感，达到翼型性能高且稳定的目的。

飞行器翼型在非设计状态下常出现性能不稳定现象。本文以一马赫数区间为非设计状态因素，进行RAE2822基准翼型的稳健设计，使稳健翼型的阻力系数对马赫数区间范围内的变化不敏感。达到不但要降低翼型的阻力还要实现翼型性能稳定即不发生阻力系数剧烈波动的目的。该目的在本文中通过对稳健翼型在马赫数区间(Ma∈[MaminMamax])的阻力系数的均值和方差进行评价，本文稳健设计参考了文献2[2]中的目标模型，本文目标模型如下所示：

(1)

式中，μ为阻力系数的均值；σ2为阻力系数的方差；D为翼型的几何外形参数；T为外形的几何约束；Cl为升力系数约束条件；R为雷诺数约束条件；α为攻角；Ma为选定的马赫数变化区间。

在稳健设计目标模型中翼型的升力系数和阻力系数都是关于翼型外性设计变量、攻角以及马赫数的函数。稳健设计的目标是获得一个在给定的马赫数变化区间内，较基准翼型的阻力系数均值和方差更小的稳健翼型。将升力系数和雷诺数作为约束条件，避免其对最终阻力系数结果产生影响。使用偏最小二乘法(Partial Least Squares，PLS)建立阻力系数关于翼型外形设计参数(D)和马赫数(Ma)的替代模型来对阻力系数进行预测。PLS替代模型可解决使用CFD软件计算阻力系数Cd时计算量过大、耗时长，甚至无法求解的问题,并能保证最终结果满足一定的精度要求。使用PLS替代模型的预测结果来获得目标模型≠2+...2的近似值，目标模型的近似值求解公式如下所示：

(2)

2 翼型稳健设计流程及各步骤原理

本文中使用偏最小二乘法建立替代模型进行翼型稳健的流程主要分为三大关键步骤：确定试验设计方法、建立替代模型和进行遗传优化。稳健设计详细步骤与设计流程图(图1)如下所示：

(1)确定稳健设计的优化目标模型。

(2)进行翼型参数化，确定外形设计因素的个数。

(3)确定试验设计方法及试验设计的因素数及其水平数，生成对应样本点数据。

(4)对试验设计样本点翼型外形生成对应网格并进行雷诺数约束下的CFD计算，获得样本点对应的阻力系数Cd值。

(5)根据CFD计算出的样本Cd的结果，使用偏最小二乘法建立替代模型。

(6)使用偏最小二乘法建立的替代模型与遗传算法结合进行寻优，得到稳健翼型外形设计参数水平值的最佳组合。

(7)计算稳健翼型外形参数所对应翼型在设定的马赫数范围内的阻力系数的均值与方差，并与基准翼型RAE2822进行比较，验证稳健翼型性能是否更佳。

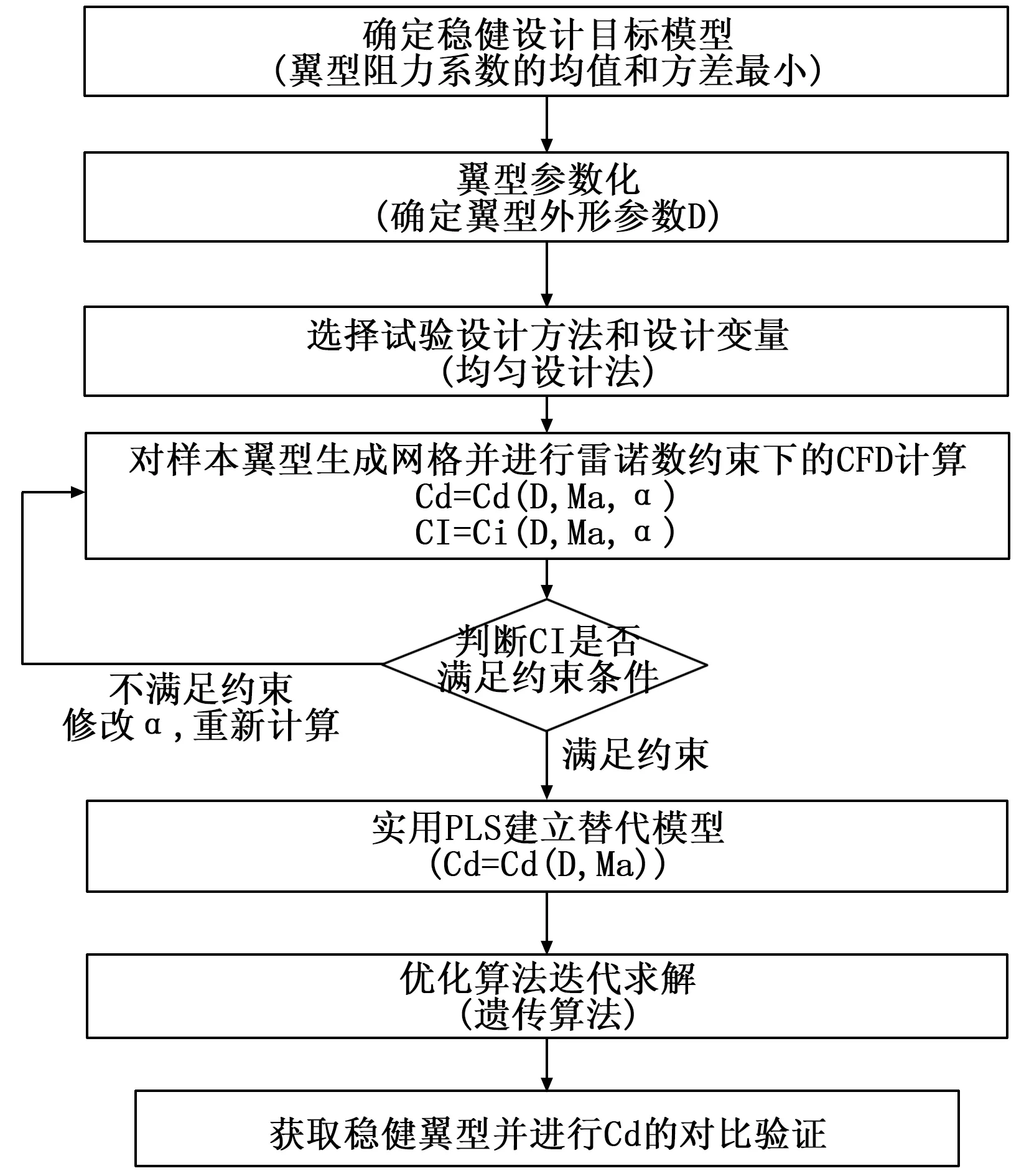
图1 PLS翼型稳健设计流程图

稳健翼型设计流程中各步骤详细介绍：

2.1 翼型外形设计参数化

在翼型外形参数化步骤中采用当前常用的Hicks-Henne[3]型函数进行线性叠加的方法来获取样本翼型的外形，样本翼型的外形是由基准翼型和型函数及其相关系数叠加生成的，Hicks-Henne生成样本翼型的公式如下所示：

(3)

式中，Fbas为基准翼型的外形数据，Pi为型函数的相关系数，即翼型外形参数的设计变量，n为选取的设计变量的个数，fi(x)为Hicks-Henne的型函数。Hick-Henne型函数的表达式如下：

(4)

2.2 试验设计方法的选取

试验设计[4](Design of Experiment)是用于对试验进行合理安排，使样本点更具代表性，减少试验次数的方法。常用的试验设计方法主要有：正交试验设计方法、均匀设计法、超拉丁方抽样法等。本文采用由我国方开泰教授和数学家王元提出的均匀设计法。均匀设计法与正交试验法相比，只考虑了试验点在试验设计范围内均匀分布，无需考虑正交试验中整齐可比的要求，其试验点的均匀性更佳，将其用于翼型稳健设计能大大减少样本点的数量。在本文中，通过马赫数和翼型外形参数的因素数及水平数来确定最合适的均匀设计表，来进行试验样本的安排。

2.3 样本翼型的网格生成及其CFD计算

对样本数据表中每一行的一个翼型样本使用Gridgen软件进行对应的二维网格生成，网格结构采用C型结构。在进行翼型样本网格生成前，需要先建立RAE2822基准翼型的结构化二维网格，为后续CFD结果正确性验证做准备。RAE2822基准翼型的C型网格如图2所示。

图2 RAE2822基准翼型网格

生成样本点翼型的网格后，开始进行对应网格的CFD[5]计算，使用气动计算中常用的Fluent软件完成。在样本翼型CFD计算前，先使用Fluent计算RAE2822基准翼型网格在雷诺数R6=6.5×106，Ma=0.73，α=3.19时的翼型表面压力分布，通过和1979年关于RAE2822的试验报告[6]中的翼型表面压力分布结果进行对比，来验证CFD计算的正确性。对比结果如图3所示，结果表明气动分析结果正确，符合精度要求。

图3 RAE2822翼型表面压力分布CFD计算和试验报告结果对比

2.4 建立偏最小二乘替代模型

建立偏最小二乘替代模型的目的是为了降低使用Fluent软件进行CFD计算时的工作量，减少求解时间。通过PLS进行回归拟合，能最快得到阻力系数目标模型值。偏最小二乘法又称偏最小二乘回归[7]，其是一种多对多的线形回归建模方法。当所求解目标的自变量和因变量数量多，且彼此存在多重相关性，而样本的数量却较少时，用偏最小二乘法获得的模型比传统回归模型，如主成分回归分析模型要更优，能提供更加深入和丰富的信息。

2.4.1 偏最小二乘法的建模原理：

假设有m个自变量{x1,x2…,xp}和n个因变量{y1,y2…,yp}。为了研究自变量x和因变量y之间的统计关系,设有k个样本点,由此获得了自变量与因变量的数据集X={x1,x2…,xp}和Y={y1,y2…,yp}。

偏最小二乘法首先分别在自变量集合X与因变量集合Y中分别提取出第一成分t1和u1(简而言之，t1是x1,x2…,xp的一个线形组合,u1是y1,y2…,yq的一个线形组合)。在提取这两个第一成分时,为了回归分析的需要,有两个需要格外关注的要求:

(1)t1和u1应尽可能多地分别提取出自变量集和因变量集中的变异信息;

(2)t1和u1间的相关程度要达到最大。

上述两个要求的目的是要使得t1和u1尽可能好的代表数据集合X和Y,同时自变量的第一成分t1对因变量的第一成分u1还要具有最强的解释能力。

在第一成分t1和u1被提取后，使用偏最小二乘法分别进行X对t1的回归以及Y对u1的回归。如果回归方程能达到满意的精度，则算法中止；否则将利用X被t1解释后的残余信息以及Y被u1解释后的残余信息进行第二成分的提取，直到能达所需要的精度为止。若最终对自变量X共提取出r个成分t1,t2…,tr，偏最小二乘法将通过建立y1,y2…,yq与t1,t2…,tr的回归,然后再表达成y1,y2…,yq关于原变量x1,x2…,xp的回归方程。

2.4.2 偏最小二乘法的简化算法步骤：

本文采用文献[10]中偏最小二乘的简化算法，能极大的减少计算时间，减小程序代码的编写难度。

为简便计算，设m个自变量{x1,x2…,xp}和n个因变量{y1,y2…,yq}均为归一化后的变量。归一化方法采用min-max方法，如下所示：

(5)

式中，i为变量范围内的一个具体变量的下标；j为变量类型下标(自变量或因变量)xjmax；xjmin和分布为自变量或因变量的最大值和最小值。

完成归一化后，将自变量集和因变量集的w次数据矩阵分别记为：

PLS简记算法的简要步骤如下：

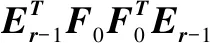
(6)

最终的n个因变量的偏最小回归方程为 ：

yj=aj1x1+…+ajmxm,j∈[1,m]

(7)

偏最小二乘法的详细步骤、推导过程及其Matlab程序代码可参考文献[10]。偏最小二乘法还可建立二次、三次等高阶多项式回归模型。本文中为获得更好的模型拟合效果，采用偏最小二乘法建立三次多项式回归模型。

2.5 遗传算法优化

本文采用遗传算法进行稳健翼型的寻优。采用马赫数按等差数列生成，其余翼型设计变量在指定范围内随机生成的办法来进行遗传算法优化求解。

遗传算法[11]是一种自适应全局搜索算法。其参考达尔文的生物进化论，通过模拟自然界中生物种群的进化发展过程，来尽可能得到全局最优解。

本文中对目标模型进行近似表示，来进行遗传算法求解：

(8)

式中，NMa为选取的马赫数区间范围内的马赫数的个数，D为翼型的外形参数变量。

在遗传算法算法计算过程中，对多个变量使用二进制的形式进行编码。遗传算法中种群的数量决定了遗传算法的多样性，种群数目越多则多样性越好，但计算量也会增加，降低运行效率。然后数目过少又可能出现局部最优解，因此需要研究人员根据具体问题进行种群数目的确定，一般种群数目最小应大于等于20。在遗传算法中变异概率(Pm)对种群的影响应远远小于交叉概率(Pc)，Pc和Pm的相关取值分析见文献[12]，Pc一般取值范围为0.4～0.99，Pm取值范围为0.001～0.1。罚函数采用的是翼型最大相对厚度的几何约束，即最大相对厚度的最大值和最小值，使用罚函数能保证最终翼型外形的合理性，以便获得最优解。将PLS替代模型和遗传算法结合以获得稳健翼型的外形设计参数的一组最佳组合，再使用Hicks-Henne型函数进行处理，即可获得稳健翼型的外形数据。

3 试验样例及其结果分析

以对RAE2822基准翼型进行稳健设计来对偏最小二乘法建立的替代模型的效果进行验证。选择在马赫数Ma∈[0.7,0.8]，雷诺数Re=6.5×106,翼型升力系数Cl=0.8，翼型最大相对厚度0.1≤d≤0.12的条件下，进行基准翼型的稳健设计。在Hicks-Henne翼型参数化时采用十个设计参数变量(d1～d10)进行翼型外形的表示(上下翼面各取五个参数变量并分别确定各设计变量的取值范围，如d1∈[-0.006,0.006]等)。马赫数是设计中除了翼型外形十个设计变量外的另一个设计变量。

完成样本CFD计算后进行偏最小二乘替代模型的建立。在PLS替代模型建立前先求取PLS模型三次多项式各系数的值，并进行保存。PLS替代模型中取NMa=1 000，即按公差为0.000 1在Ma∈[0.7,0.8]，选择种群规模M= 100,交叉概率Pc= 0.8,变异概率为pm= 0.1，进化代数步长Pd= 50，初始种群进化代数=Pd。当某进化步长的整数倍时的最佳翼型的目标模型值与临近左右步长的最佳翼型的目标模型值相等时，即目标模型值不再发生变化时，停止种群进化迭代。将稳健翼型的外形设计变量组合的值带入Hicks-Henne中，获得稳健翼型的外形数据，并生成对应的二维结构化网格。按公差为 0.001在中生成100个马赫数，使用Fluent计算稳健翼型分别在这100个马赫数以及升力系数、雷诺数约束下的Cd值，计算出阻力系数的均值与方差并与基准翼型在同样条件下的均值和方差进行对比，以验证稳健翼型的效果是否更优。

图4 遗传算法进化次数及对应目标模型近似值

遗传算法计算环境为个人PC，硬件环境：处理器 2.7 GHz Intel Core i7，内存16GB 2133MHz LPDDR3；软件环境 Python 3.7.1，PyCharm 2018。遗传算法的进化次数的计算结果如图4所示，可以发现在进化次数为250次时，第200次的目标模型的近似值已与第150次和第250次的值相等，不再发生改变，已求得遗传算法的最优解，停止进化迭代。遗传算法的最终进化次数250次，用时112分钟30秒。遗传算法的最终结果如表1，可以看到偏最小二乘法建立的替代模型与遗传算法结合获得的稳健翼型在时，稳健翼型阻力系数的均值与方差都明显小于RAE2822基准翼型的数值，说明使用偏最小二乘建模方法获得的稳健翼型的效果更佳，偏最小二乘法建立替代模型的方法确实可以用于翼型的稳健设计之中。

表1 PLS稳健翼型与基准翼型阻力系数均值和方差对比

图5为PLS稳健翼型与RAE2822基准翼型的外形对比，可明显发现稳健翼型的厚度有所减小，上表面更为平坦，因此其出现阻力发散的临界马赫数将提高，最大相对厚度的减小能带来翼型波阻的减小，使性能得到提升。此外稳健翼型下表面后缘出现了一个非常明显的向里凹进去的反曲断，表明稳健翼型具有了明显的超临界翼型的特征，后缘反曲断的出现使后缘的升力增加，弥补了由于上表面平坦而引发的升力不足问题。在图6翼型性能比较图中，可明显发现PLS稳健翼型在升力系数和雷诺数约束下且处于设定范围时，其阻力系数明显小于基准RAE2822翼型的阻力系数值。从最终结果来看，PLS建立的替代模型达到了翼型稳健设计的目标。

图5 PLS稳健翼型与基准翼型的外形对比

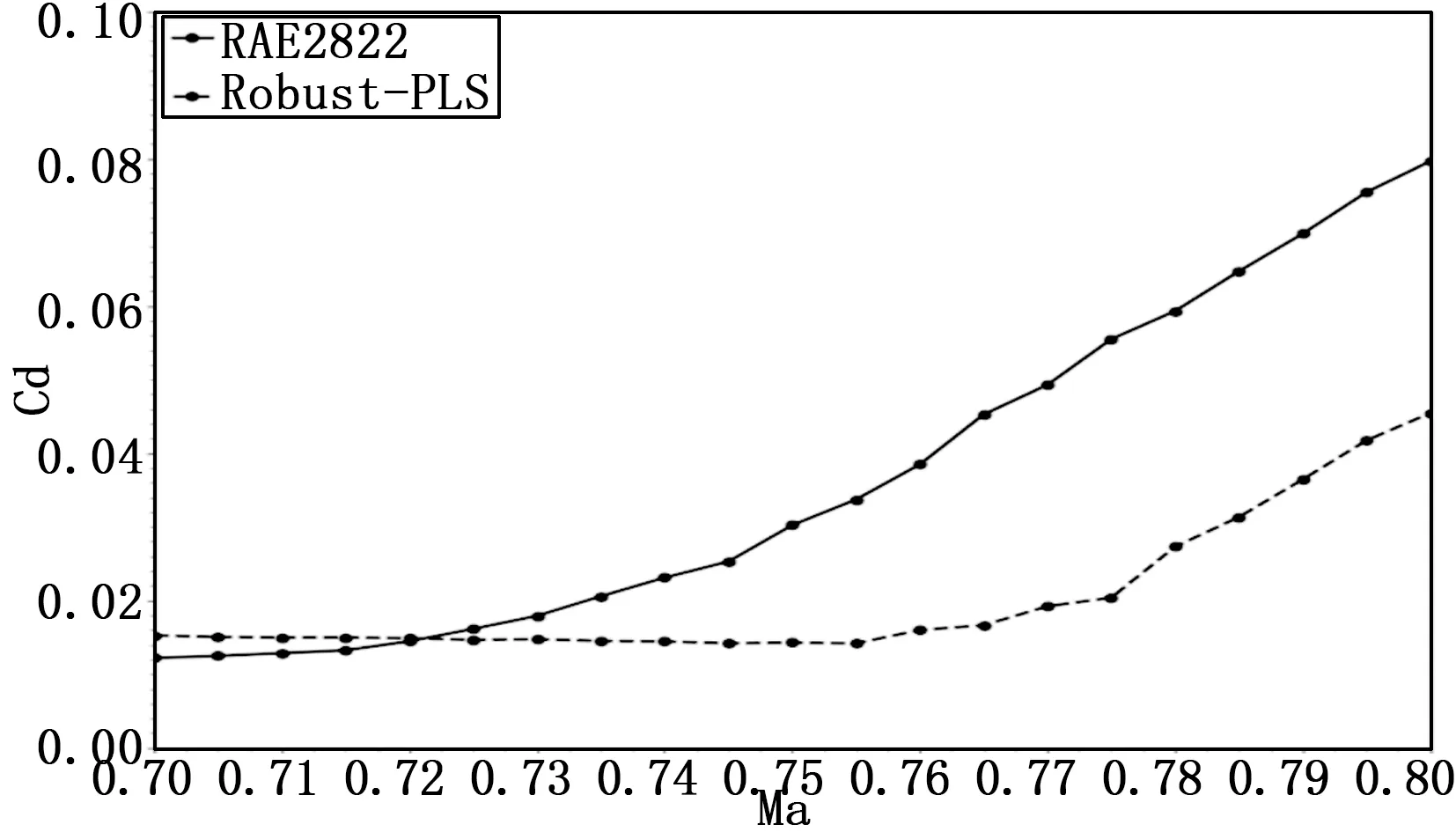
图6 PLS稳健翼型与基准翼型的性能对比

4 结论

本文使用偏最小二乘法建立替代模型来解决传统飞行器翼型设计中存在的单点设计和CFD计算量过大，风洞试验成本高的问题。以获得某一区间变化的马赫数(即外界环境不稳定)下翼型阻力系数均值和方差最低的翼型稳健设计为研究背景，通过偏最小二乘法建立替代模型来完成翼型的稳健设计，实现在保证一定精度下，稳健设计快捷和简易的目标。结果表明，采用PLS替代模型方法，能有效实现本文翼型稳健设计计算成本低，计算快，精度能保证的目的。

在后续的研究中，还可将PLS替代模型方法用于机翼的稳健设计以及风力机叶片稳健设计、发动机叶片稳健设计中。飞行器翼型的稳健设计结果可为后续机翼和整机的稳健设计打下了良好的基础。偏最小二乘替代模型在稳健设计上具有广阔的应用前景，值得深入研究。