基于改进DNN-LSTM算法的车辆前方行人行为识别方法

(上海工程技术大学 机械与汽车工程学院，上海 201820)

0 引言

随着汽车保有量的快速增加，交通事故数量和死亡人数一直处于较高水平，行人作为道路交通的主要参与者，保障行人安全是智能交通系统建设的重要目标之一。资料数据表明，在道路交通事故的人员伤亡中，行人横穿道路发生的交通事故占较大比重。因此，实现对行人行为的有效检测和正确识别，可保障交通环境中行人的安全，减少交通事故的发生率[1-2]。实现车辆前方行人行为的准确识别是汽车自动驾驶系统构建基本要求，对改善道路交通安全和交通质量具有重要的意义[3]。

车载摄像系统可对车辆前方的行人及道路状况进行记录，通过对记录的视频数据进行分析可识别出行人的行为动作[4]。根据视频数据源不同可将行为识别方法划分为三类：基于彩色视频的行为识别、基于深度图的行为识别、基于骨架节点的行为识别[5]。基于彩色视频的行为识别方面，Feichtenhofer等人[6]提出了一种新的双流网络时空结构，将时间流和空间流产生的特征在时间和空间上进行3D融合识别视频，但由于数据集中的干扰信息过多对识别精度产生了一定的影响。基于深度图的行为识别方面，Vieira等人[7]在识别行为动作中，保留了时空单元之间的空间和时间的上下文信息，具有较高的灵活性。与前两种方法相比，基于骨架节点的行为识别方法主要利用骨架的运动特征表示行为，具有更好的视图不变性，减小了识别模型的复杂度和计算量[8]。Yang等人[9]利用人体关节点位置的差异性，提出了一种由特征信息构成骨架节点的表达方式，并作为特征描述符，利用朴素贝叶斯分类器进行行为识别。Boulbaba等人[10]使用中值滤波方法对骨架节点的轨迹进行平滑处理，并分别用最近邻分类器和支持向量机对动作进行分类。Zhang等人[11]采用关节线距离作为输入，以较少的训练样本数量获得较好的识别结果。Zhu等人[12]提出了一种端到端完全连接的长短时记忆网络用于基于骨架的行为识别。基于骨架节点的行为识别方法能够有效的降低行为识别复杂程度，但由于其特征数据中包含干扰序列，致使该方法识别精度方面仍存在一定的改善空间。

综上所述，本文以骨架节点为研究对象，建立了基于经验模态分解(Empirical Modal Decomposition, EMD)的深度神经网络-长短时记忆网络(Deep Neural Network-Long Short Term Memory, DNN-LSTM)行为识别模型。该方法结合了经验模态分解能够平滑数据的优点，采用深度神经网络对数据做特征分析，并利用长短时记忆网络对获取的行为特征做时序分析，从而实现对车辆前方行人行为的准备识别。

1 骨架节点特征提取

骨架节点特征提取是行人行为识别的关键技术之一。该方法首先以行人行为骨架节点为基础，提取行人行为运动的关键参数，构建行人行为特征表征向量。势能、加速度以及位置信息等特征在识别行人的行为动作方面具有很强的表述性。选取势能、相对位置、加速度、角加速度作为表征参量描述行人行为，表征形式δi如公式(1)所示。

δi=[Eij,Pi,ai,γi]

(1)

式中，Eij为骨架节点的势能变化特征；Pi为相邻帧间同一关节点处的相对位置特征；ai为节点加速度特征；γi为关节点处角加速度特征。

为解决人与摄像机相对位置不同出现的误差，利用相邻帧间的势能差来表示行人势能的变化[13]，在行人的运动过程中，头部相对肢体其他部位坐标变化较小，故选取头部作为零势能点,人体的势能变化表示如公式(2)所示。

Eij=L(Pi,j-Pi,0)

(2)

式中，L为势能参数，取9.8；Pi,j为第i帧中的第个骨架节点的像素；Pi,0为第i帧中零势能点的像素。

不同运动情况下，相邻两帧间各骨架节点的相对位置变化量不同，其表达式如公式(3)所示。

Pi=Pi,j-Pi-1,j

(3)

式中，Pi-1,j为i-1帧第个骨架节点的像素。

行人动作可以看作一组骨架节点组成的刚体轨迹，不同的运动方式其速度与加速度会产生不同的变化，且变化差异较大。速度与加速度表达式如公式(4)所示。

(4)

式中，dt为相邻两帧之间的时间间隔；根据姿态估计算法性能，此处取为。

每个刚体的运动可看作是以刚体长度为半径的圆周运动，都有对应的角速度和角加速度[14]。以膝盖处的角速度和角加速度为例：设大腿处的向量为rm,小腿处的向量为rn，则关节角弯曲角度表达式如公式(5)所示。

(5)

式中，rm，rn分别为相邻的两向量；||为向量的模。

刚体的角速度及角加速度表达式如公式(6)所示。

(6)

式中，αi,j为当前帧膝盖处的弯曲角度；αi-1,j为前一帧的膝盖处的弯曲角度。

2 基于EMD的DNN-LSTM模型

针对提取的特征数据存在干扰信息以及需要考虑特征信息的时序性等问题，提出了基于EMD的DNN-LSTM网络识别模型。该方法主要基于经验模态分解方法对初始特征数据进行平滑处理，利用深度神经网络对特征数据做非线性变换，并采用长短时记忆网络分析连续帧间的变化规律。

2.1 模型原理

EMD[15]具有自适应特性，能够根据数据自身的特征进行分解，把数据中包含大尺度的波动逐级分解开，用于处理非线性、非平稳性数据，并将各分量能量小于某一阈值的数据滤除达到数据去噪的目的。

其分解假设满足两个条件：在整个时序内，分量的局部极值点和零点的数目之差小于或相等1个；在任意时刻，局部极大值点形成的上包络线和局部极小值点形成的下包络线，均值为零。其分解步骤如图1所示。

图1 分解步骤

每个分量代表一个特征尺度的数据序列，分解过程即将原数据序列分解成各种不同特征波动序列的叠加。利用能量法根据提取的特征数据以及各分量的能量占比选择合适的阈值M对数据进行处理，使特征数据更加平稳以利于后续识别阶段的处理。

计算各分量的能量：

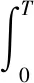
(7)

式中，T代表每个动作的总帧数。

计算各分量的能量占比：

(8)

式中，Ki为第i个信号IMF分量的能量比；I为信号分量的个数。

经过上述处理特征数据可以表示为：

(9)

式中，cj为原始信号的第j个分量；rn为原始信号的残余分量。

考虑到模型的网络性能和泛化能力，增加网络层数可以提高精度但会使网络复杂化，增加节点数会降低误差，因此改进模型的深度神经网络有4个隐含层，每个隐含层有32个神经元。但深度神经网络对特征的处理在各时刻都是独立的，循环神经网络对特征的处理具有时序性，其神经元在当前时刻的输入包括上一层神经元在该时刻的输出和自身在前一时刻的输出。长短时记忆网络[16]在循环神经网络的基础上加入了门控机制，其细胞单元中包含输入门、遗忘门和输出门。

图2 DNN-LSTM模型

当深度神经网络具有l层网络，其第l-1层共有m个神经元时,则第l层的第j个神经元的输出表达式如公式(10)所示。

(10)

式中，tanh为神经元的激活函数；σ为sigmoid函数；ω为权重系数；δ表示当前层的输入；b为偏置向量。

本文序列帧长度为N的特征序列δ=(δ1,δ2,…,δn)，标准LSTM单元按时间顺序从t=1-n进行计算其计算公式如公式(11)～(16)所示。

遗忘门决定细胞单元中遗忘的信息，输出一个0-1之间的数值输入到输入门，计算公式为：

(11)

式中，ht-1为上一个细胞的输入；δ为DNN的输出即LSTM当前细胞的输入。

输入门决定需要更新和丢弃的信息，分三步运算，σ决定更新的数据，tanh得到一个新候选值，决定加入到细胞状态的比例，计算公式为：

(12)

(13)

(14)

输出门是LSTM的最终输出，先利用决定更新再与得到的新候选值相乘获得最终输出，计算公式为：

(15)

ht=ot*tanh(ct)

(16)

DNN输出更明显的特征向量后利用LSTM分析其时间序列特性[17]。对人体左右两侧分别进行特征提取，模型输入层的节点数n=8，深度网络层的节点数为32，激活函数为tanh函数，长短时记忆网络层的神经元个数为64，激活函数为sigmoid函数，输出层的节点数为1，激活函数为sigmoid函数。为解决过拟合问题，实现更有效地学习加入Dropout层，其比重设置为0.5。图3为融合的神经网络模型图。

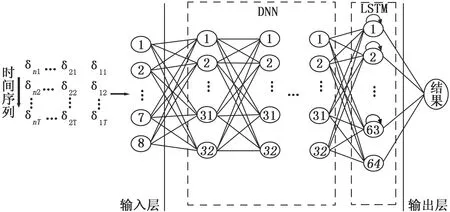
图3 网络模型图

2.2 模型的训练

有监督训练在训练过程中既有训练数据又有训练结果，训练效果较好，因此采用有监督训练，将处理好的特征输入模型中，经过模型处理得出相应的识别结果。本文模型采用均方误差函数(mean square error，MSE)作为损失函数，即将预测值与实际值作比较，利用损失函数计算识别结果与真实值之间的误差。具体表达式如公式(17)所示。

(17)

计算数据的损失梯度后，优化算法对损失进行优化，模型使用的优化算法是自适应学习率的Adam优化算法，利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率，一阶矩估计的指数衰减率为0.9，二阶矩估计的指数衰减率为0.999，使每一次迭代学习率都有明确的区间，参数较平稳，可较快预估结果。

3 实验结果与分析

3.1 Weizmann数据集

Weizmann数据库包含了10个动作，每个动作有9个不同的样本，视频的视角是固定的，背景中没有嘈杂的环境。文中主要针对交通过程中行人的常见行为即行走和奔跑进行识别，将数据集中的剩余行为作为负样本数据集进行处理。原始视频数据经过前期预处理后分为训练集和测试集两部分。其中，训练集用于建立模型和调整参数，测试集用于测试模型的识别精度，训练过程中用2/3的动作数据作为训练数据，1/3的动作数据作为测试数据。

3.2 预处理结果分析

对视频中的动作利用一种自下而上的人体姿态估计算法[18]获取人体各关键点的像素点，该算法检测人体的十八个关键的骨架节点，是特征提取的基础。图4为对实际场景中行人检测的序列图。

图4 行人运动序列图

图5和图6分别为跑步和行走时的足部轨迹图。从图5中的前14帧以及15帧到30帧，可以看出行人的运动轨迹呈周期性变化，从图6中可以看出左右脚的位置呈互补关系，证明检测算法的准确性和可靠性较高。对某一帧骨架节点像素值全为零的情况，利用前两帧的数据变化规律进行补缺的方法填补特征数据。

图5 跑步时足部轨迹图

图6 行走时足部轨迹图

3.3 实验结果分析

为了校验基于改进DNN-LSTM算法的车辆前方行人行为识别模型的有效性，采用常用的传统DNN模型、LSTM模型以及DNN-LSTM模型作为对比模型。对比试验采用相同的试验数据作为输入，对比结果如图7至图8及表1所示。图7为各模型在整个训练过程中随着训练迭代次数增加的损失变化图，图8为精度变化图，为了能更清晰直观的比较各个模型的损失与精度之间的差异，从迭代30次后进行对比。

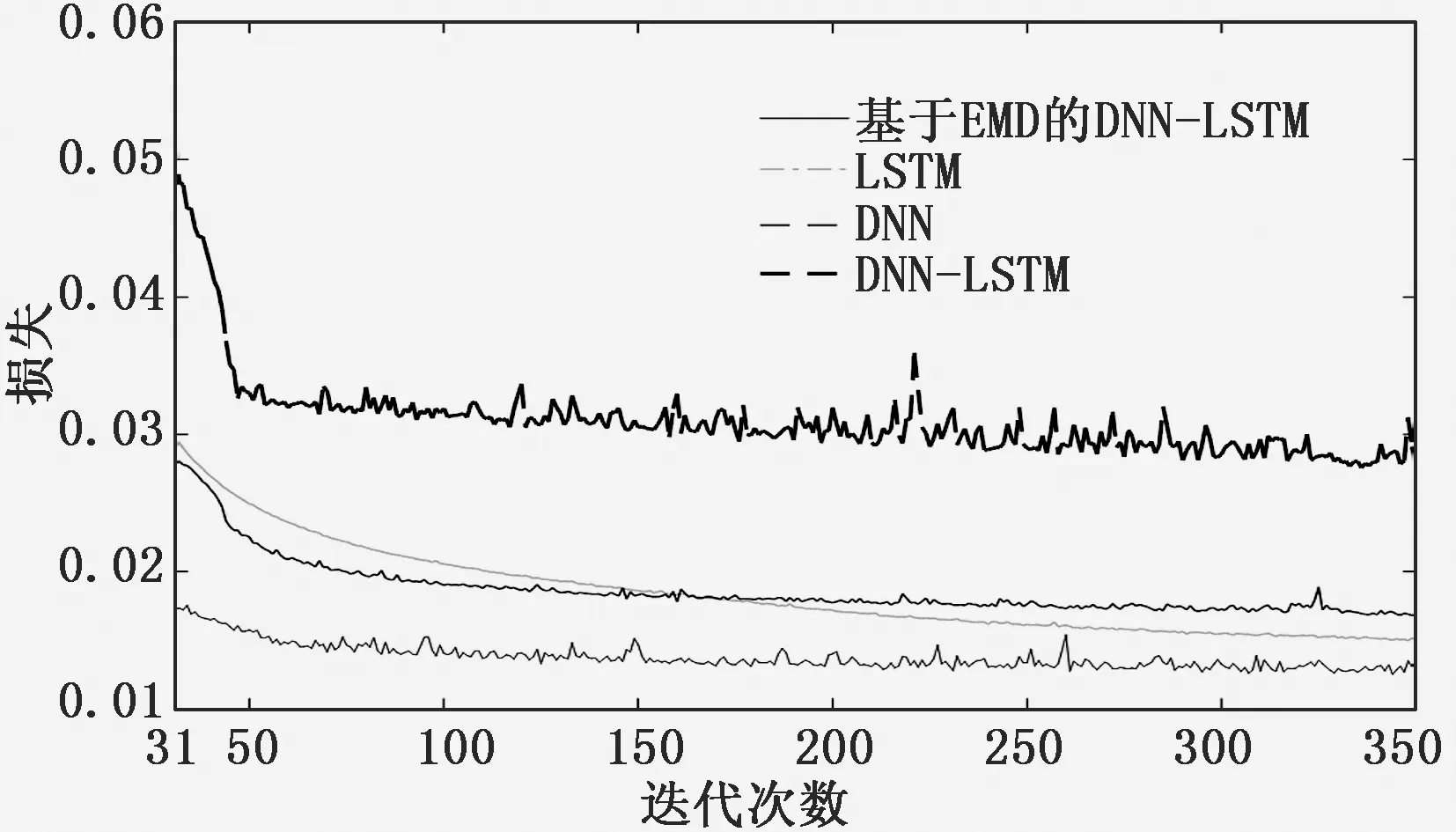
图7 各模型训练损失图

图8 各模型精度图

从图7中可以看出，在训练过程中基于改进DNN-LSTM算法的网络模型在迭代150次左右已趋向稳定，趋于稳定的速度明显快于其他模型，且其损失值比其他3种模型更小。未经平滑处理的特征数据在训练过程中的损失较大，证明特征数据平滑处理的必要性；其余3种模型均用预处理后的特征数据做为训练模型的输入，损失下降过程中波动较小，且损失值与未经预处理的模型相比下降0.01左右。

图8可以看出，随着迭代次数增加精度均呈增加的趋势，在迭代次数达到100次左右时精度趋于稳定。传统DNN模型在迭代过程中精度上升最慢；未经EMD处理的模型的精度波动最大，平稳性较差；改进DNN-LSTM算法的网络模型识别精度明显高于其他3种模型，且训练后期稳定性较好。

表1为对Weizmann数据集进行行为识别的准确率与其他模型的识别准确率对比表，从表中可以看出识别准确率由高到低依次为：改进自行车的DNN-LSTM、DNN-LSTM、LSTM、DNN。在特征提取阶段简化了识别模型的输入，减少了模型输入的参数量，模型的计算效率有所提高。改进DNN-LSTM算法的网络模型识别准确率要高于其他3种类型，主要原因是对特征进行了平滑处理以及用LSTM网络进行时间序列分析；并证明改进DNN-LSTM算法模型可提高行为识别的准确率。

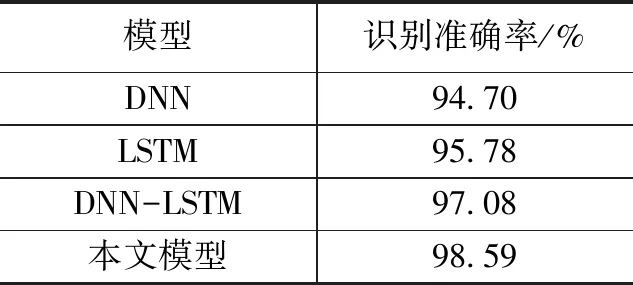
表1 与其他模型识别准确率对比表

为证明模型的可行性，采用KTH数据集对模型进一步训练和测试，KTH数据集由25个人在4个不同场景下进行的6类动作组成，共有2391个视频样本。视频样本的外在环境变化包括尺度变化、衣着变化和光照变化，将慢跑与跑步视频作为跑步数据集，行走作为行走数据集，剩余行为作为其他负样本数据集，数据集的前期处理与Weizmann数据集相同，最终的识别部分依然用数据集中2/3的动作数据作为训练数据，1/3的动作数据作为测试数据。识别精度达到98%，证明本模型在KTH数据集上也同样适用。

4 结论

本文提出了一种基于EMD的DNN-LSTM的深度学习模型进行行为识别。提取关键骨架节点的特征向量后利用EMD降低特征数据的不平稳性，最后用DNN-LSTM模型实现行为识别，模型表现出不错的识别效果。

(1)为评估新模型的性能，分别在DNN、LSTM、DNN-LSTM、改进的DNN-LSTM四个模型上利用Weizmann数据集进行训练与测试，结果表明新模型的测试识别率达到98.59%，高于其他3个模型。

(2)新模型在KTH数据集的测试精度达到98%，证明该模型适用于两种数据集，具有较高的可行性。由于实验中采用的数据集背景比较单一，且均为单人动作，与现实场景有所偏差，未来将对复杂环境下的多人场景进行行人的行为识别。