砂箱弥散试验尺寸效应及弥散度尺度效应

宫 玥，张 敏，任 宇，郭彩娟，孙 琳,3

(1.中国地震灾害防御中心,北京 100029；2.中国地质科学院水文地质环境地质研究所，河北 石家庄 050061；3.自然资源部地下水科学与工程重点实验室，河北 石家庄 050061；4.中国地质大学(北京)水资源与环境学院,北京 100083)

0 引 言

弥散度是孔隙含水层中污染物迁移的关键参数，表征介质的弥散特征，主要是介质非均质性的体现[1-5]。然而，弥散度获取一直以来都是水文地质学的难点问题[1-5]。室内砂箱弥散试验是获取弥散度的重要手段[5-11]。但室内试验测得的弥散度不仅与含水介质有关，还受试验规模影响。室内所测得的弥散度往往与野外测定的相差一个或数个数量级[5-9]。因此，一般认为，砂箱、土柱等室内弥散试验可用作研究水动力弥散机理，不可应用于野外[1-10]。

普遍认为，室内试验不可应用于野外的原因是弥散度尺度效应。研究发现，尺度越大，弥散度越大[1-5]。依此理论，砂箱尺度获取的弥散度经尺度分析可外推至野外尺度。然而，外推至野外尺度涉及穿越不同尺度约束体系的限制问题，该问题虽已在多个学科领域研究数年，至今却仍是世界性难题，尺度外推常被认为是砂箱弥散试验野外应用的主要制约问题[12-15]。尺度外推需要首先刻画砂箱尺度对试验结果的影响。野外弥散度主要体现土体的非均质性，而砂箱由于边壁存在，其弥散度体现的则是砂箱边壁和土体二者组合的非均质性[16-20]。理论上可认为，砂箱边壁影响产生的尺寸效应越小，试验结果越接近土体弥散度。若砂箱尺寸越趋于无限大，边壁影响几乎可忽略，则可通过尺度分析外推至野外应用。但实际是否如此仍未见试验研究。总之，尺度效应和尺寸效应限制了砂箱弥散试验的野外应用，尺寸效应及其对尺度效应的影响到底如何有待研究。

本文采用不同尺寸的大、小砂箱，以NaCl为示踪剂，开展砂箱一维水动力弥散试验[5-11,21-25]，分析大、小砂箱弥散度特征，以导向性方法表征弥散度尺度效应和砂箱尺寸效应及其二者关系，为消除尺寸效应对砂箱试验测定土体弥散度影响，实现砂箱试验弥散度的野外尺度外推应用提供参考。

1 材料与方法

1.1 试验设计及砂箱装置

试验设计大、小两个尺寸类型砂箱(图1)。将大砂箱视为具理想无边壁影响的无边界条件，无砂箱尺寸效应；以大砂箱为对照，小砂箱视为具边壁影响较大的有边界条件，产生尺寸效应；同等尺度下，弥散度的差异即为尺寸效应导致的。为尽量符合以上理想模式，弥散试验观测孔设置在纵向中心线上，使得弥散度观测受砂箱边壁非均质性影响最小。并且，为验证试验代表性，同类型砂箱设置平行对照，大、小砂箱各2个，共4个砂箱。基于此设计思路制作的大、小砂箱含水层分别为1.0 m(长)×0.4 m(宽)×0.6 m(高)、0.5 m(长)×0.2 m(宽)×0.3 m(高)，大砂箱尺寸为小砂箱的两倍，每10 cm设置一个观测孔。

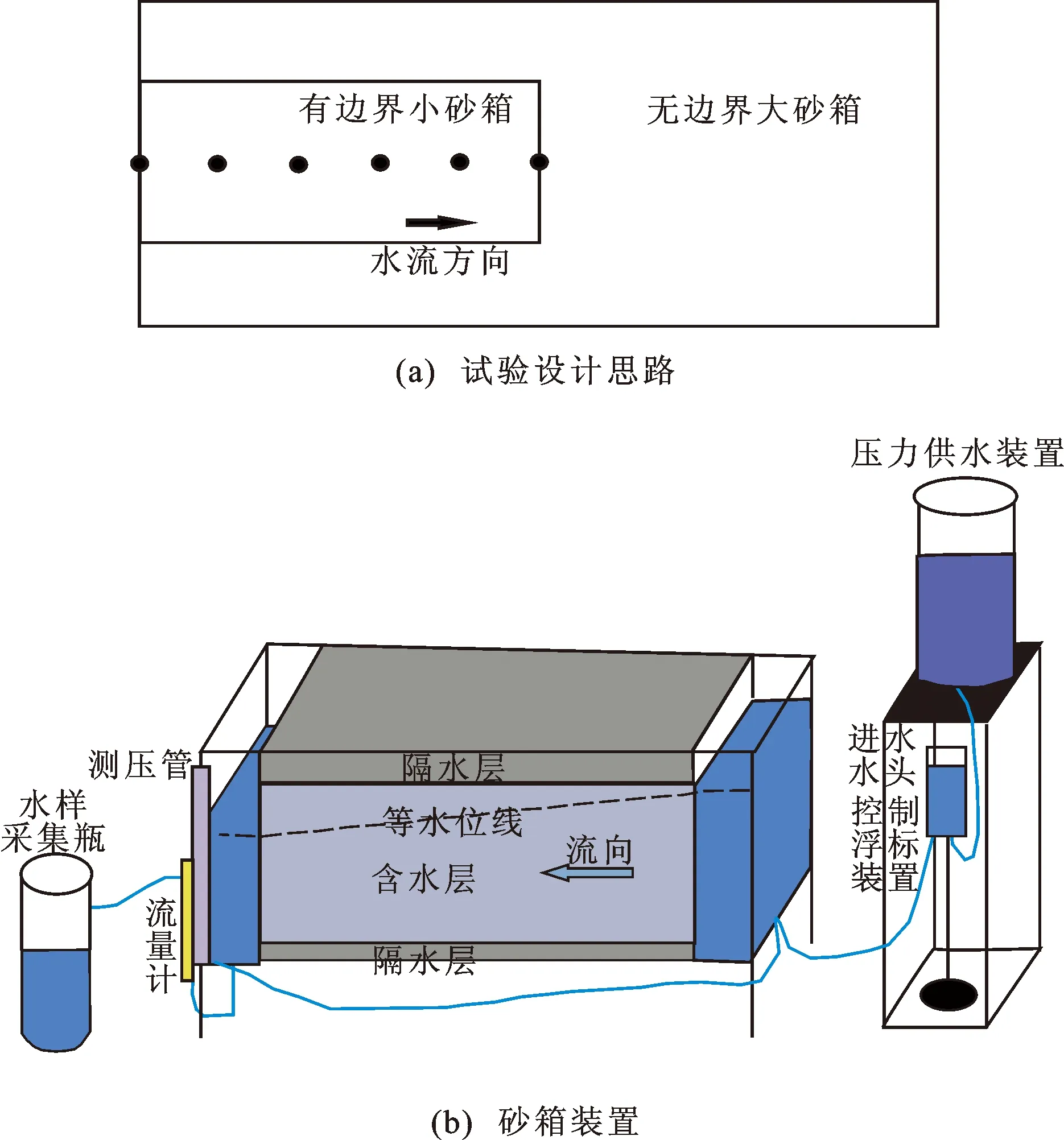
图1 试验设计思路及砂箱装置示意图

整个砂箱试验装置还包括压力供水装置，进水水头控制浮标装置，进、出水缓冲水箱，出水系统4部分装置。①压力供水装置：砂箱供水装置为提供约两倍于砂箱进水水头(随着水桶液面变化而变化)的蓄水桶，与进水水头控制浮标装置进水口连接，保证提供足够水压使浮标正常运作，提供稳定供水(图2)。②进水水头控制浮标装置：水箱下端分为进水口和出水口，进水口为压力供水装置与浮标阀门连接点，出水口与砂箱水箱体连接；当出水口水输入砂箱水箱体，则浮标上层空气浮力组件下沉，带动反作用杠杆将浮标阀门打开，由于供水装置与浮标进水口存在水头差而将水补入浮标装置，从而保证水头稳定[图3(a)]。③进、出水缓冲水箱(缓冲水箱的宽度为0.1 m)：经进水水头控制浮标装置的水首先进入进水缓冲水箱，防止直接进入砂箱，形成局部压力流网；同理，出水口设有出水缓冲水箱[图3(b)]，保证整个过水断面出水，防止产生局部压力流网。④出水系统：由出水缓冲水箱出水后，连接阀门浮球流量计，可调节流量，观测实时流速；然后，连接至进水水头高度固定的水样采集瓶；砂箱进、出水缓冲水箱底部预留了两个测压管连接出口，以软管连接至同一砂箱位置，测定水头差(图4)。

图2 压力供水装置

1.2 砂箱含水层及达西渗流试验

提供试验的含水层土体样品为华北山前平原子牙河流域滹沱河冲洪积扇砂土。大砂箱上、下各10 cm填充粉土，作为相对隔水层，中间40 cm为中、细砂填充的含水层；小砂箱上、下各5 cm填充粉土，作为相对隔水层，中间20 cm为中、细砂填充的含水层。填土前，过40目筛网，砂土粒径不超过0.425 mm。填土过程中，每添加10 cm厚度砂层，加水至饱和，自然沉积压实7 d，再继续填土，重复以上操作，直至填满砂箱。连续通水30 d，排除气体；观测流量，连续5 d流量稳定，视砂箱土体已压实，砂箱中水不再排空。通入地下水为华北山前平原深层地下水(中国地质科学院水文地质环境地质研究所饮用深层地下水)。

图3 进水水头控制浮标装置及出水缓冲水箱

图4 出水系统

根据达西(Darcy)定律，渗透系数表达式为

K=v/I

(1)

式中：K为渗透系数；I为水力坡度；v为达西流速。

开展8个水力坡度在10-3数量级((1～4)×10-3)的一维稳定渗流试验。线性回归水力坡度与达西流速关系发现，判定系数(R2)为0.988 2(图5)，拟合较好，土体渗透系数为17.226 m·d-1，在此范围内地下水流动满足达西定律。

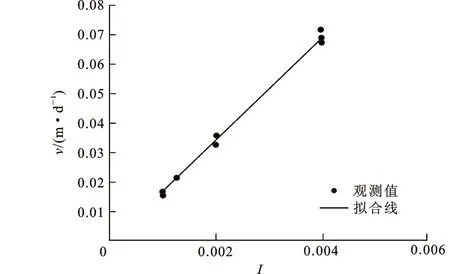
图5 水力坡度与达西流速的关系

1.3 弥散试验

接上述达西渗流试验，持续通水，将各砂箱水力坡度进一步调控，使其接近上述回归分析中段范围(水力坡度为(2～3)×10-3)，开展一维稳定渗流弥散试验。根据压力供水装置、进水水头控制浮标装置和进水缓冲水箱体积，添加NaCl至浓度2 g·L-1，开始初始浓度恒定的一维稳定渗流弥散试验，依据文献[2]和[7]，选取解析解方法计算弥散度。采用电导率仪监测示踪NaCl浓度。NaCl浓度和电导率关系见图6，其判定系数为0.996 5。监测砂箱纵向中心线离进水口分别为10、20、30、40 cm时观测孔中的电导率。当示踪剂到达某观测孔，则开始每5 h监测一次，直至达峰值稳定状态[24]。

图6 NaCl浓度与电导率的关系

2 弥散度计算结果

以流量和NaCl浓度绘制弥散正态分布函数，函数符合标准正态分布，则按以下方法计算弥散度[2,7]。其表达式为

式中：U为液体流出体积与试验柱体积比；u为实际流速；L为柱体长度；Q为流量；A为过水断面面积；n为有效孔隙度，取0.3；t为从开始进水至测样时间；C为电导率；Cc为实测电导率；Cb为电导率本底；t0.5为相对浓度达到0.5时的时间；D为弥散系数；α为弥散度；J0.84、J0.16表示C/C0值为0.84、0.16时对应的J值；C0为添加浓度电导率。

从弥散正态分布(图7、8)可看出，所有正态分布拟合优度的判定系数为0.815～0.985，均大于0.81(一般认为是极强相关)，基本满足标准正态分布，计算得到的弥散度见表1。

3 结果分析

3.1 砂箱试验获取弥散度的特征

表1中弥散度计算相关结果显示，大砂箱1、大砂箱2、小砂箱1、小砂箱2试验条件下地下水实际流速分别为0.449、0.737、0.602、0.511 cm·h-1，变异系数为0.22。按一般经验，孔隙渗流状态基本一致，差异不大，且理论上弥散度并不受流体特征影响，主要是受介质空间结构非均质性的影响[1-5]，因此，可认为不同尺度试验条件下弥散度的变化是弥散度尺度效应和砂箱尺寸效应的表征。统计所有测得的弥散度，其范围为1.00～6.67 cm，均值为3.06 cm，变异系数为0.54，差异明显，说明砂箱试验存在明显的弥散度尺度效应和(或)砂箱尺寸效应。

简单统计大、小砂箱弥散度的均值分别为1.78、4.33 cm，小砂箱弥散度大于大砂箱；大、小砂箱弥散度范围分别为1.00～2.82、3.00～6.67 cm，所有小砂箱的弥散度均大于大砂箱。这说明小尺寸弥散度大于大尺寸，换而言之，砂箱尺寸越小，尺寸效应越明显。大、小砂箱弥散度变异系数分别为0.40、0.29，大砂箱大于小砂箱；大砂箱1、大砂箱2、小砂箱1、小砂箱2在10、20、30、40 cm不同尺度下的变异系数分别为0.36、0.49、0.30、0.18，所有大砂箱的变异系数均大于小砂箱。这说明大砂箱弥散度随尺度变化更大，换而言之，砂箱尺寸越大，尺度效应越明显。

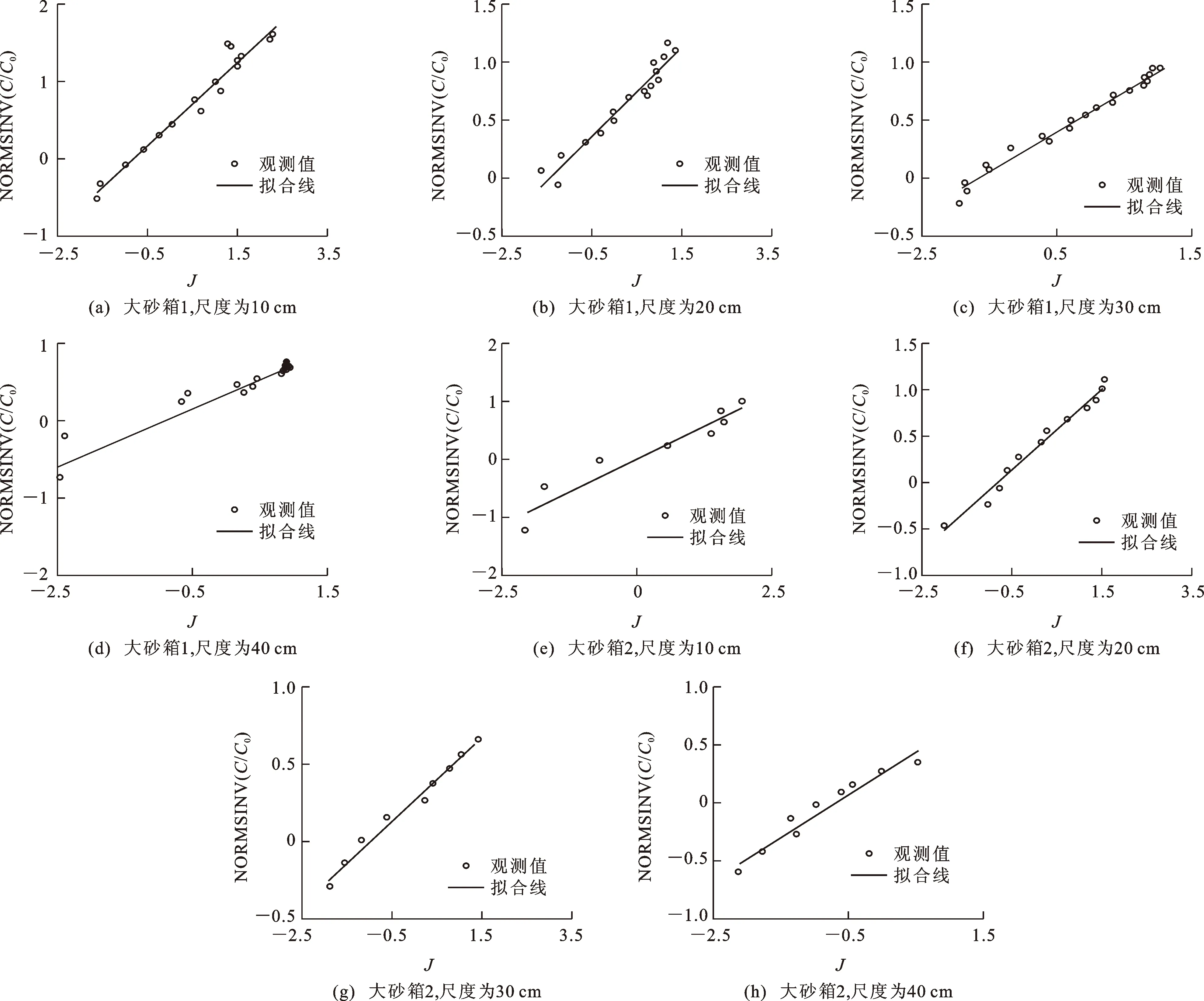
图7 大砂箱试验不同尺度弥散正态分布

图8 小砂箱试验不同尺度弥散正态分布

表1 弥散度计算结果

Tab.1 Calculated Results of Dispersivity

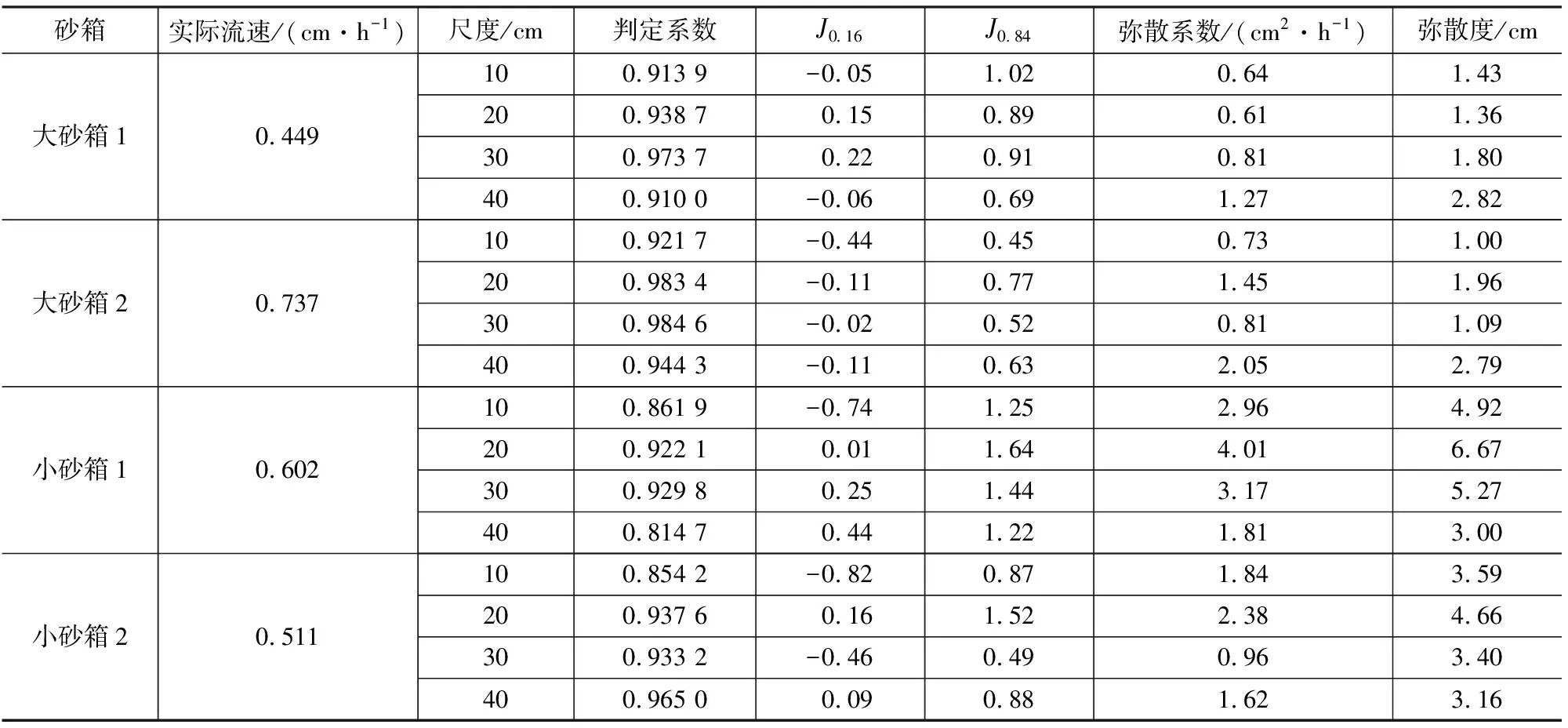
砂箱实际流速/(cm·h-1)尺度/cm判定系数J0.16J0.84弥散系数/(cm2·h-1)弥散度/cm大砂箱10.449100.913 9-0.051.020.641.43200.938 70.150.890.611.36300.973 70.220.910.811.80400.910 0-0.060.691.272.82大砂箱20.737100.921 7-0.440.450.731.00200.983 4-0.110.771.451.96300.984 6-0.020.520.811.09400.944 3-0.110.632.052.79小砂箱10.602100.861 9-0.741.252.964.92200.922 10.011.644.016.67300.929 80.251.443.175.27400.814 70.441.221.813.00小砂箱20.511100.854 2-0.820.871.843.59200.937 60.161.522.384.66300.933 2-0.460.490.963.40400.965 00.090.881.623.16

3.2 尺度效应对弥散度的影响及其表征

理论上，天然条件下，尺度越大，弥散度越大[1-5]。计算可知，10、20、30、40 cm不同尺度下，大砂箱弥散度分别为(1.21±0.30)、(1.66±0.42)、(1.45±0.50)和(2.81±0.03)cm，小砂箱弥散度分别为(4.26±0.94)、(5.66±1.42)、(4.33±1.32)和(3.08±0.11)cm。以该弥散度均值±误差为纵坐标，以尺度为横坐标，绘制弥散度随尺度变化曲线(图9)，并以回归斜率量化尺度效应。尺度效应的物理意义量化为尺度每增加1 cm，弥散度增大多少厘米。尺度效应表达式为

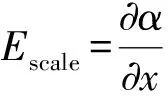
(2)

式中：x为尺度；α为弥散度；Escale为尺度效应,以大砂箱为表征，其尺度效应为0.045 7。

图9 弥散度随尺度变化

砂箱试验条件下，大、小砂箱弥散度随尺度变化均不严格遵循尺度效应规律，砂箱尺寸可能影响了弥散度的尺度效应。趋势上，大砂箱尺度越大，弥散度越大，线性回归判定系数为0.696 5，基本满足尺度效应规律；小砂箱尺度越大，弥散度越小，线性回归判定系数为0.351 9，不满足尺度效应规律。大砂箱尺度效应对弥散度的影响可以α=0.045 7x+0.640 2方程表示，小砂箱则不可以线性回归斜率量化尺度效应。

与第3.1节分析结果吻合，该现象表明：虽然砂箱尺寸影响了弥散度的尺度效应，但相对小砂箱而言，大砂箱受尺寸效应影响小，即大砂箱弥散度尺度效应明显，小砂箱弥散度受尺寸效应控制，尺度效应被掩盖。

含水层弥散度的本质是溶质迁移过程由达西流速(平均速度)与每一点孔隙速度的差值引起溶质的空间分异现象[1-3,22]。对于地下水溶质迁移的弥散度尺度效应，主要是非均质性引起的。该砂箱试验虽然采用均质砂，但含水层随尺度增加，非均质性仍增加，弥散度受砂箱尺寸效应显著。此为该试验条件下弥散度尺度效应的主要原因。

3.3 尺寸效应对弥散度的影响及其表征

在第3.2节分析大砂箱受尺寸效应影响较小的基础上，视大砂箱基本不受尺寸效应影响。在此以(αs-αl)/αl量化砂箱尺寸效应，其中，αs为小砂箱弥散度，αl为大砂箱弥散度，αs-αl为砂箱尺寸导致的弥散度。在试验条件下，尺寸效应的物理意义量化为砂箱尺寸由1.0 m×0.4 m×0.6 m变为0.5 m×0.2 m×0.3 m，长、宽、高尺寸均减至1/2，同等尺度下弥散度增大的倍数。其表达式为

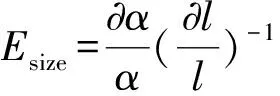
(3)

式中：l为砂箱的尺寸；Esize为尺寸效应。

砂箱尺寸变化指长、宽、高等比变化，表达式中砂箱的尺寸取砂箱长度。

在10、20、30、40 cm尺度下，尺寸效应分别为-5.02±0.78、-4.82±1.00、-3.98±1.14、-0.20±0.10，呈减小趋势。从砂箱尺寸效应对弥散度影响的柱状图及误差线(图10)可看出：10、20、30 cm尺度下，与大砂箱相比，小砂箱弥散度分别增大(2.51±0.39)倍、(2.41±0.50)倍、(1.99±0.57)倍，但3个尺度下的误差重叠；与其他3个尺度相比，40 cm尺度下的误差无重叠，小砂箱弥散度仅增大(0.10±0.05)倍。

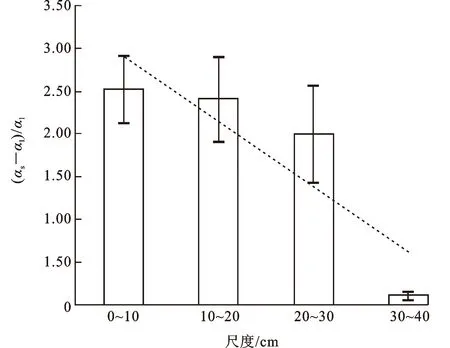
图10 尺寸效应对弥散度的影响

3.4 尺度效应与尺寸效应的关系

理论上，砂箱边壁与土体的非均质性产生的尺寸效应是一定值。若尺度无限大，则尺寸效应产生弥散度的占比较少，表观上砂箱尺寸效应消失[16-20]。从图10可以看出，试验条件下，随着尺度增大，大、小砂箱弥散度相差倍数越来越小，尺度效应与尺寸效应存在一定关系。以尺度为横坐标，大、小砂箱弥散度相差倍数为纵坐标作线性回归分析，发现判定系数为0.772 3，拟合优度较高。其回归方程为

(4)

Esize=0.153 2x-7.331 8

(5)

以式(5)外推预测，尺度为48 cm时，尺寸效应为0。

4 结 语

(2)本研究仅为室内条件获取弥散度的应用提供导向性方法。从试验本身而言，实际上，大砂箱尺寸效应是客观存在的，砂箱尺寸效应导致弥散度的刻画相对保守。换而言之，大砂箱的尺度效应回归方程并不严谨。基于此的尺度效应、尺寸效应及二者关系的量化表征均并不严谨。加之，试验观测尺度及观测孔数量有限，趋势分析可认为明显，但严格讲，其统计意义不足，尤其是尺寸效应的外推预测有待验证。尺寸效应和尺度效应关系产生的机理模型也有待研究。

砂箱试验设计得到了中国地质科学院水文地质环境地质研究所陈宗宇研究员的指导与帮助，砂箱弥散试验得到河北地质大学郭跃龙同学的协助，在此一并表示感谢。

[第41卷卷终]