退化的C型量子群Uq(sp2l,2m)
陈学鑫 成 锦
( 山东师范大学数学与统计学院,250358,济南 )
1 引 言
量子群[1-4]是近年来新兴的数学分支,是在研究量子力学中的量子可积系统时提出来的.其表示理论可以产生Yang-Baxter方程的解,进而来构造扭结不变量.量子群理论在许多数学领域和数学物理领域都有广泛的应用[5-8],例如:可积模型,共形场论,低维拓扑[9,10]和表示理论[11]等.我们在本文中提出了量子群Uq(sp2n)的退化形式Uq(sp2l,2m),研究了它的Hopf代数结构和元素间的交换关系.
2 退化量子群Uq(sp2l,2m)的定义
任意给定一组正整数m,n,其中n>m+1,令l=n-m.设集合I={1,2,…,n},且令p=-q-1,当a≤m时,令qa=q;当m (1) (2) (3) (4) eaeb=ebea,fafb=fbfa,若|a-b|>1, (5) (6) (7) (8) (9) (10) emEm-1,m+2-Em-1,m+2em=0 , (11) fmEm+2,m-1-Em+2,m-1fm=0, (12) 其中Em-1,m+2和Em+2,m-1是由以下关系来定义的: Em+2,m-1:=fm+1Em+1,m-1-qm+1Em+1,m-1fm+1, Em+1,m-1:=fmfm-1-qmfm-1fm. Δ(ea)=ea⊗ka+1⊗ea,Δ(fa)=fa⊗1+ka-1⊗fa,Δ(kb)=kb⊗kb; 令 Q+:=emEm-1,m+2-Em-1,m+2em,Q-:=fmEm+2,m-1-Em+2,m-1fm, fbQ+-Q+fb=0,ebQ--Q-eb=0, ∀b∈I, (13) (14) (15) 为了更进一步的分析Uq(sp2l,2m)的结构,我们用惯用的记法来表示x-交换 [A,B]x=AB-xBA, 对于∀A,B∈Uq(sp2l,2m)和x∈C(q).显然这也包含了李代数中[A,B]=[A,B]1的情况. 给出量子伴随表示的定义: ad:Uq(sp2l,2m)⊗Uq(sp2l,2m)→Uq(sp2l,2m), (16) x⊗yadx(y):=∑(x)x(1)yS(x(2)). 现在对于任意的1≤i Eji=Ej,j-1Ej-1,i-qj-1Ej-1,iEj,j-1,对于j>i+1. 基于当|a-b|>1时,fa与fb可交换的事实,有 Eji=EjkEki-qkEkiEjk=[Ejk,Eki]qk,其中j>k>i+1, 进一步观察到: [fi,fi-1]qi=fifi-1-qifi-1fi=-qiadfi-1(fi), 通过定义中的Serre关系,可得到任意两元素之间的交换关系[13]. 引入一个自同态ω: 根据定义1,显然可以得到定理1. 定理1F(θ)K(η)E(θ)是代数Uq(sp2l,2m)的一组生成元. 通过对退化量子群Uq(sp2l,2m)的研究,我们得到了其较好的代数性质,这为以后量子超群的研究提供了新的思路.接下来的工作是继续研究在特殊点(比如在长根处)退化的情况,进一步搞清退化版本与相应的量子超群间的区别与联系.另外将C型退化量子群的定义推广到B型和D型中,我们可以进行更深入的研究.



3 Uq(sp2l,2m)的Hopf代数结构与元素间的交换关系








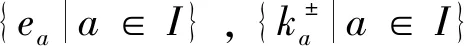







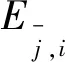



4 结 语

