受限状态下的高速列车迭代学习控制方法研究

何之煜,杨志杰,吕旌阳

(1.中国铁道科学研究院研究生部,北京 100081； 2.中国铁道科学研究院集团有限公司通信信号研究所,北京 100081； 3.北京邮电大学信息与通信工程学院,北京 100876)

迭代学习控制(Iterative Learning Control， ILC)是在有限区间内处理重复运行系统跟踪控制问题最有效的方法之一，其特点是原理简单、易于实现且对模型要求不高，是一种近乎无模型的前馈学习控制算法。自1978年日本学者Uchiyama提出迭代学习控制理论至今[1]，国内外专家学者对其做了大量的工作[2-5]，逐步形成了具有严格数学描述的控制理论体系。目前，对迭代学习控制的研究和应用已遍及工业生产的方方面面，如工业机器人[6，7]、数控机床[8]、工业化学反应堆[9]、注模机[10]、列车自动驾驶系统[11]和汽车防抱死系统[12]等。

高速列车自动驾驶系统是一个具有高度重复性的控制系统，具体表现为运行环境的重复性、运行计划的重复性、运行目标的重复性以及列车动力学模型的重复性。文献[13]首次将ILC思想引入到列车自动驾驶系统中，文献[14]研究了距离域反馈、迭代域前馈学习的列车自动驾驶控制方法，基于距离域建模，结合压缩映射方法，控制列车逐渐逼近期望轨迹。文献[15]提出预测迭代学习控制算法来处理系统输入受限问题，实现对期望轨迹的精确跟踪，但需要知道控制系统的精确模型。文献[16]设计了一个动态建模的ILC算法，通过递推最小二乘法辨识模型参数，基于范数最优理论，实现对跟踪误差关于2范数收敛，但没有考虑系统初态和受限问题。

系统受限问题普遍存在于现代工业控制系统中，主要表现为输入受限和状态受限。目前，对于控制系统受限问题下的迭代学习控制研究已有了大量的研究成果，文献[17]设计了一个双环ILC控制器来解决系统输入受限问题，ILC环1用来学习标称系统的控制器，ILC环2则用来拟合非线性控制输入项，但是双环结构复杂且独立工作。文献[18]以受限状态下的Euler-Bernoulli梁结构为研究对象，在非周期性分布式扰动和边界扰动作用下，建立了基于时间加权的Lyapunov-Krasovskii能量函数，实现了跟踪误差沿迭代轴的渐进收敛。文献[19-20]将饱和函数sat(·)引入输入受限控制系统的研究中。文献[21]针对一个线性状态受限的系统，将迭代学习控制问题转化为凸函数优化问题，证明了算法的跟踪误差是关于2范数收敛的，但是没有对非线性系统进行深入研究。文献[22]利用双曲正切函数和饱和函数处理机械手控制系统输入受限问题，实现跟踪误差随迭代轴的渐进收敛。

与大多数工业控制系统相同，高速列车自动驾驶系统也是一个受限的控制系统，主要体现为执行器物理结构对控制输入的限制、线路的固定限速和临时限速等。本文充分考虑上述限制因素，针对时变、非线性的高速列车自动驾驶控制系统，提出一种受限状态下的迭代学习控制算法，建立类Lyapunov函数的复合能量函数，对所设计的算法的收敛性进行证明，通过计算机仿真验证，证明了算法的有效性。

1 问题描述

为便于描述，通常将列车看作是一个刚性质点，理想状态下的列车动力学模型可以表示为

(1)

式中，i为系统迭代运行次数；x1，i(t)为列车运行距离，m；x2，i(t)为列车运行速度，m/s；f(Xi，t)为列车运行的单位非线性阻力函数，N/kg；b为系统的输入增益，这里取列车的质量的倒数1/M；ui(t)为列车的输入牵引力/制动力，kN；fb(t)为列车的单位基本阻力，N/kg；fa(s)为线路上的单位附加阻力，包括坡道附加阻力fg、曲线附加阻力fc和隧道附加阻力ft，N/kg；a0，a1，a2分别为列车基本阻力函数的系数。

列车在实际运行过程中会受到以下两方面的限制。

(1)输入受限

umin(t)≤ui(t)≤umax(t)

(2)

式中，umax(t)，umin(t)分别为系统控制输入的上、下界。

(2)状态受限

xk，min(t)≤xk，i(t)≤xk，max(t)

(3)

式中，k为系统阶数，k=1，2；xk，max(t)，xk，min(t)分别为系统状态信息的上、下界。

考虑系统受限情况，可以将式(1)改写为

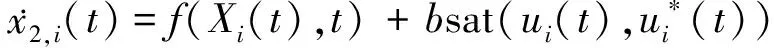
(4)

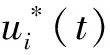
(5)

本文的控制目标是，对于给定的列车运行期望曲线xd，在式(2)、式(3)限制条件下，基于迭代学习控制理论，找到一个最优的控制序列ui(t)，使得当i→∞时，系统能够精确跟踪期望曲线。

为方便控制器设计，提出如下合理假设。

假设1：列车在每次运行前满足相同的初始条件，即

Xi(0)=Xd(0)， ∀i∈Z*

(6)

假设2：存在一个最优的控制序列ui(t)，使得列车能够在有限时间t∈[0，T]内完全跟踪上期望的轨迹曲线。

为便于对下一节控制器收敛性的分析，这里给出关于饱和函数的性质。

(7)

2 控制器设计

在设计控制器之前，首先定义系统的跟踪误差ei(t)=xi(t)-xd(t)，进一步，系统在第i次迭代的扩展误差可以表示为

si(t)=c1e1，i+e2，i

(8)

定义系统第i次迭代的Lyapunov函数为

(9)

上式关于时间t求导，可得

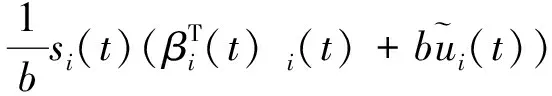
(10)

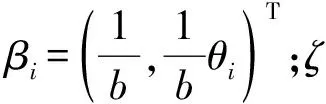
为满足Lyapunov稳定性要求，对于重复运行的列车自动驾驶系统，基于迭代学习的思想，在受限情况下，设计如下控制器

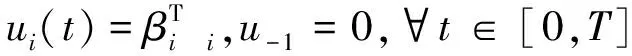
(11)

时变的模型系数向量βi可以通过饱和函数和迭代学习的思想来实现，表示为

(12)

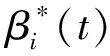
3 收敛性分析

针对高速列车自动驾驶系统，给出所设计控制律的收敛性分析，下述定理是主要的结论。

定理1：对于高速列车自动驾驶系统模型式(1)执行重复运行任务时，应用迭代学习控制器，本文所设计的控制律和学习增益更新律具有以下的性质。

(L1)∀t∈[0，T]，当迭代次数i趋向于无穷时，跟踪误差向量ei(t)趋向于零。

(L2)系统状态信号ui(t)，xi(t)均有界，且在任意时刻任意迭代次都能满足约束条件(2)和(3)。

证明 首先，构造类Lyapunov的复合能量函数(为了表述清晰，会对函数的表达作一定的简化)

(13)

式中，δβi为时变学习增益的估计误差，δβi=β-βi。

接下来，分别对定理1中的(L1)、(L2)部分进行证明。

(1)定理1中(L1)部分的证明

首先，在迭代域对复合能量函数Ei(t)进行差分，得到

ΔEi(t)=Ei(t)-Ei-1(t)=

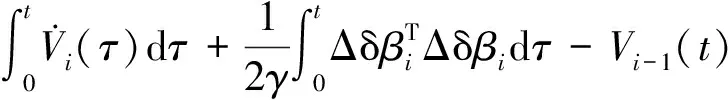
(14)

式中，Δδβi为δβi在迭代轴的差分，Δδβi=δβi-δβi-1。

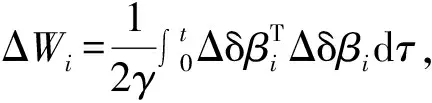
(βi-1-βi)dτ=

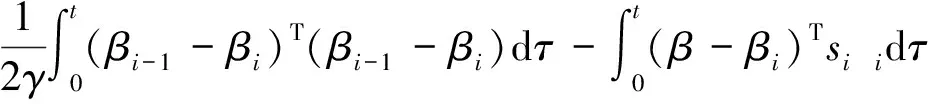
(15)

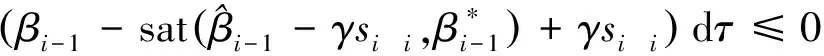
(16)

成立。

因此，利用上式可以将式(15)改写为

(17)

对式(14)第一项，将控制律式(11)代入，可以得到

(18)

将上两式代入到式(14)中，得

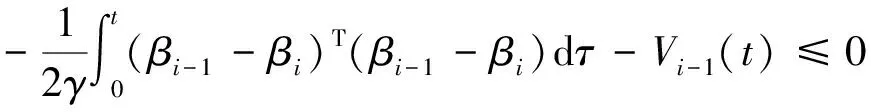
(19)

由于上式中两项均具有正定性，因此式(19)成立，即能量函数沿迭代轴具有差分负定性。

接下来，将对E0(t)的有界性进行证明。令i=0，将式(13)重写为

(20)

对上式关于时间t求导，可得

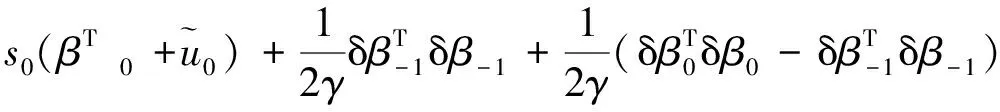
(21)

考虑到∀t∈[0，T]，β-1=0，可以将上式改写为

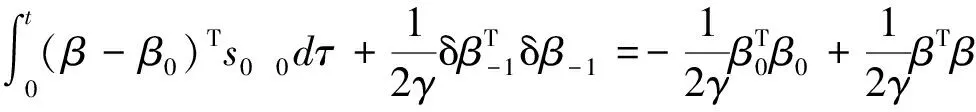
(22)

因此，可以得到

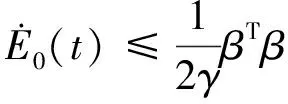
(23)

由于β为已知闭区间上的连续函数，且有界，因此，必然存在一个已知上界D*，使得

(24)

那么，式(20)就可以表示为

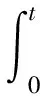
(25)

根据复合能量函数Ei(t)的差分负定性，可以将第i次迭代学习的能量函数表示为

(26)

对上式两端取极限

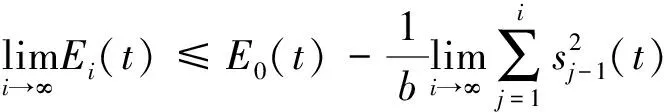
(27)

由于能量函数Ei(t)是正定的，且E0(t)在时域[0，T]上有界，所以根据级数收敛的条件，可以得知，当迭代次数i趋于无穷时，有

(28)

即列车运行的跟踪误差在迭代域上会逐渐收敛到零。

(2)定理1中(L2)部分的证明

由于能量函数Ei(t)的正定性，且E0(t)在时域[0，T]上是有界的，那么根据式(27)，Ei(t)在时域[0，T]上也是有界的。另外，根据上述的级数收敛定理，当迭代次数i趋于无穷时，系统跟踪误差ei(t)也会收敛到零。根据学习增益更新律式(12)，在饱和函数意义下，可以得出结论，时变的学习参数向量βi(t)同样是有界的。

此外，基于迭代学习控制的控制目标可达性可以描述为存在一系列的控制输入ud(t)，使得系统可以完全跟踪上期望运行曲线。那么，对于∀t∈[0，T]，系统状态xd(t)是有界的。又由于系统实际的控制状态可以描述为xi(t)=xd(t)+ei(t)，根据ei(t)的有界性，可知，系统状态xi(t)也是有界的，由此可知，控制输入ui(t)同样是有界的。

4 算例仿真

以高速动车组某型车作为仿真对象，仿真线路长度为112.46 km，计划运行时间为1 800 s。列车线路上受到的附加阻力如图1所示，根据列车动力学模型和线路条件，求解出列车在区间的期望速度曲线和期望位移曲线，如图2所示。通过Matlab仿真，将PID控制算法和D型迭代学习控制算法，与本文提出的受限状态下的迭代学习控制算法进行比较，验证算法在受限状态下的有效性和收敛性。

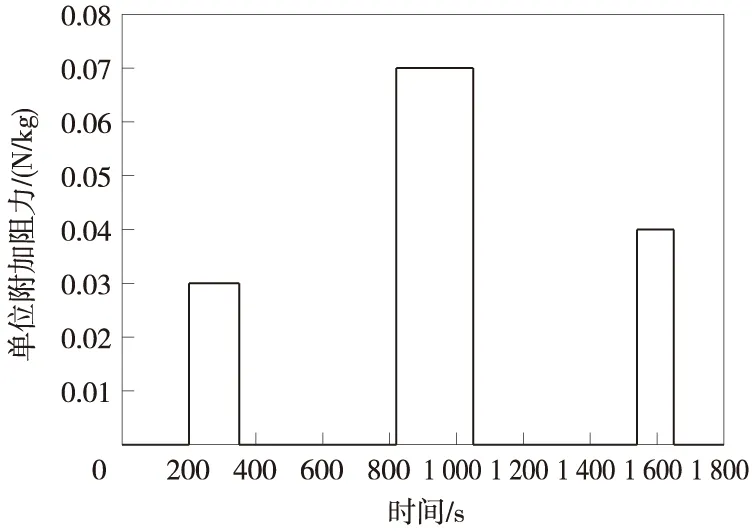
图1 列车单位附加阻力

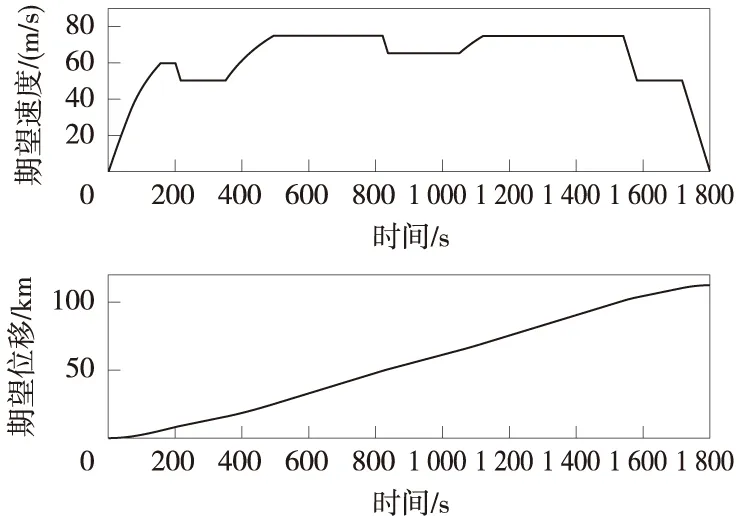
图2 列车运行期望速度和位移曲线

(1)PID反馈控制算法

工业上广泛使用PID反馈控制器，控制律设计如下

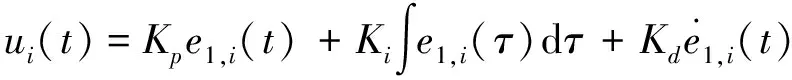
(29)

式中，Kp为控制器的比例项系数，取0.5；Ki为控制器的积分项系数，取0.1；Kd为控制器的微分项系数，取10。

(2)D型迭代学习控制算法

列车的初次迭代采用(1)的PID反馈控制器得到，从第2次开始，采用如下D型迭代学习控制器

(30)

式中，G为常学习增益，G=[g1，g2]T，取g1=1.5，g2=3。

(3)本文提出的参数化迭代学习控制算法

列车的初次迭代同样采用(1)的PID反馈控制器，根据所提出的迭代学习控制律和参数更新律，设置c1=1，θi(0)=[0，0，0]T，参数向量θ(t)的上界定义为θmax(t)=[1，0.01，0.000 5]T，下界定义为θmax(t)=[0.01，0.001，0.000 05]T，参数更新增益矩阵γ=[0.01，0.000 4，0.000 000 4]T。

图3 PID控制跟踪效果

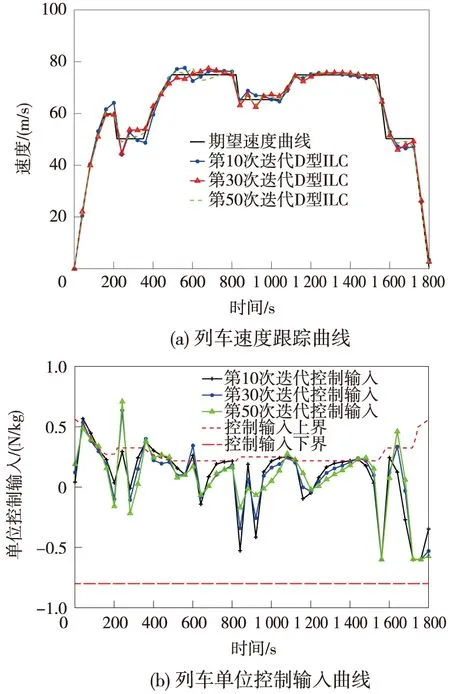
图4 D型迭代学习控制跟踪效果

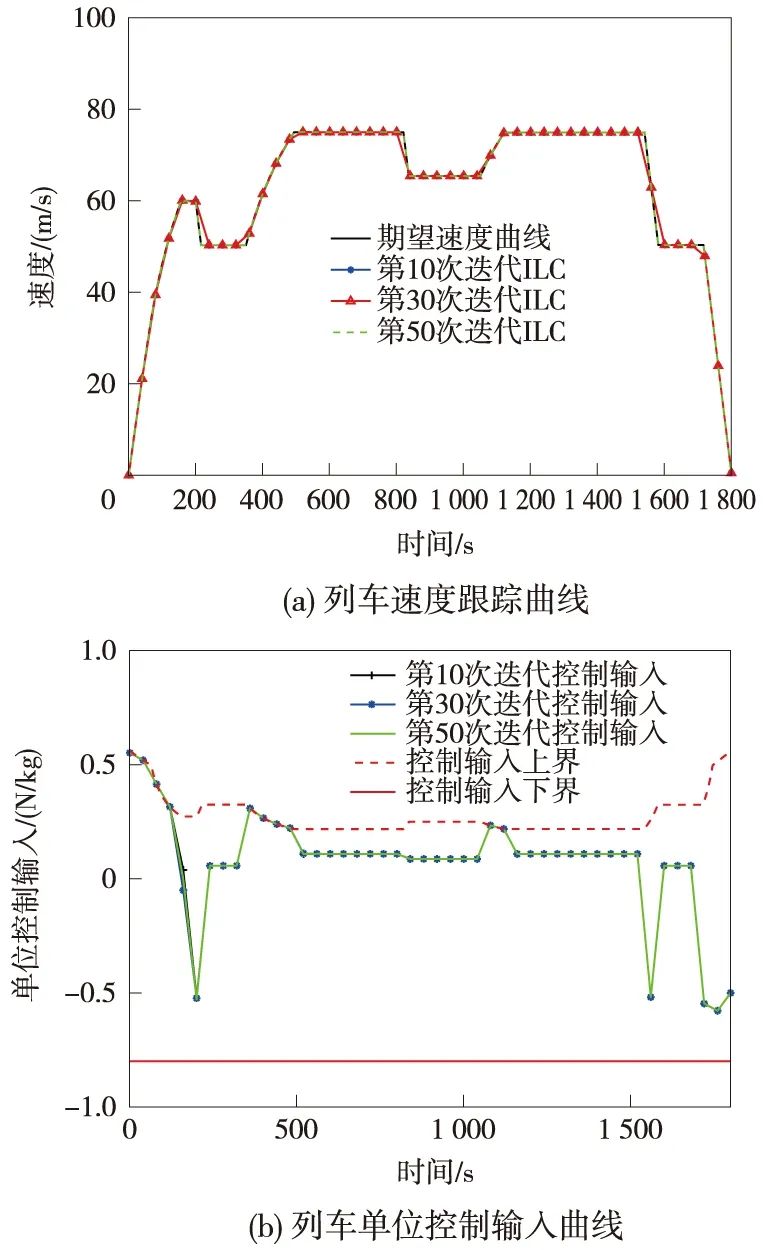
图5 本文所提出的迭代学习控制跟踪效果

由图3～图5可以看出，当列车进行工况转换时，PID反馈控制会产生较大的暂态，导致列车运行偏离期望轨迹；而D型迭代学习控制器对期望曲线跟踪的收敛速度较慢，且控制输入会超过执行器上界，不利于列车安全运行；而本文提出的受限状态下的迭代学习控制算法，通过饱和函数sat(·)的作用，保证列车运行控制输入和状态始终在允许范围内，并且能够较快地跟踪上期望轨迹曲线。

图6 三种控制算法的距离跟踪误差对比

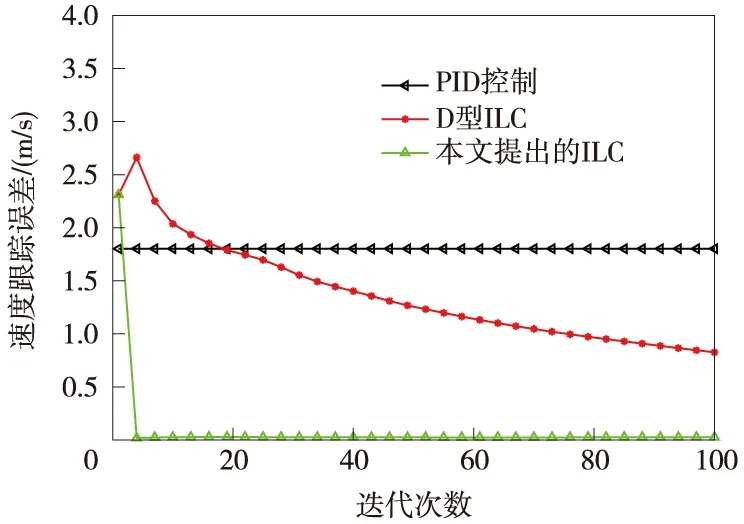
图7 3种控制算法的速度跟踪误差对比

图6和图7给出了3种控制算法在距离和速度跟踪误差的对比图，可以看出，PID算法由于没有学习机制，无法随着迭代次数提高距离和速度的跟踪精度；D型迭代学习控制算法由于没有对控制系统模型的学习，因此跟踪收敛速度较慢；而本文提出的迭代学习控制算法，可以很好的学习系统的重复性信息，达到较快的收敛速度和跟踪精度。

5 结论

为分析在受限状态下高速列车的跟踪控制问题，首先建立了在受限状态下的列车动力学模型，然后根据扩展误差建立Lyapunov函数，推导出基于迭代学习控制的控制律和参数更新律，并给出严格的数学收敛性分析，最后通过计算机仿真对所提出的算法进行验证，分析其对期望运行轨迹的跟踪性能，主要结论如下。

(1)饱和函数sat(·)可以有效限制列车自动驾驶系统执行器的控制输入过大问题，保证了系统的运行安全。

(2)通过严格的数学证明，验证了所提出的控制律沿迭代轴可以达到渐进收敛，证明了算法收敛性和稳定性。

(3)通过计算机仿真验证以及与PID算法和D型迭代学习控制算法对期望运行轨迹跟踪性能的比较，证明所提出的算法具有较快的收敛速度和较高的跟踪精度，且能够保证控制输入在允许的范围内。