滚动活塞压缩机运动副摩擦模型的研究现状

郑 贤 ，王 潇 ，韦 为 ，3，冯文波 ，石冬宇 ，谭华中

（1.广西大学机械工程学院，广西 南宁 530004；2.东风汽车集团有限公司技术中心，湖北 武汉 430058 3.广西制造系统与先进制造技术重点实验室，广西 南宁530004）

0 引言

滚动活塞压缩机具有结构简单、体积小、重量轻和动平衡性能好等诸多优点，被广泛应用于现代制冷与空调系统当中，但其效率相对其他类型的压缩机并无明显优势，这是因为影响其效率的因素较多，包括有间隙泄漏、吸排气压力损失、运动副的摩擦损耗和电机效率等[1-3]，其中运动副的摩擦损耗在滚动活塞压缩机的消耗功当中占了1/3左右[4]。摩擦损耗直接影响机械效率，要降低压缩机的摩擦损耗，其关键在于根据滚动活塞压缩机的实际工况，从现有摩擦学研究得出的摩擦模型中选择适合滚动活塞压缩机运动副实际工况的摩擦模型，建立滚动活塞压缩机运动副的摩擦模型，进而探明运动副的摩擦机理和摩擦特性。在滚动活塞压缩机中，存在摩擦的运动副主要有滑片-滑槽副、滑片-端盖副、滑片-滚动转子副、滚动转子-端盖副、滚动转子-气缸副和滚动转子-曲轴副。这些运动副在压缩机的实际运行过程中均处在动态变化的环境，即位置、温度、间隙、气体压力、润滑状态等都在不断的变化，因此，各运动副的摩擦特性实际上是一个关联多个因素并伴随工作进程而不断变动的特性。由于研究深度、认识程度和着重点等诸多方面的差异，不同研究人员对滚动活塞压缩各运动副开展摩擦特性研究时，所用的摩擦模型各不相同，没有一致的观点，为此，本文先对摩擦学自开展理论研究至今的摩擦模型研究情况进行梳理，接着对近年来关于滚动活塞压缩机运动副摩擦模型建立和摩擦特性方面的研究进行综述，最后结合作者的一些研究结论提出滚动活塞压缩机各运动副在摩擦模型建立和摩擦特性研究上的一些总结和展望。

1 摩擦模型

摩擦特性从Leonardo（1519年）的研究开始，已经被学者们研究了500多年。众多的试验研究揭示了摩擦具有丰富的行为特性，根据摩擦力可否用微分方程描述，可将摩擦模型分为静态摩擦模型和动态摩擦模型[5]。静态摩擦模型是一种摩擦力为相对速度的函数模型；动态摩擦模型是摩擦力为相对速度和位移函数的模型，因为动态模型既可以描述摩擦的静态特性，也可以描述摩擦的动态特性，故也可认为静态摩擦模型是动态模型的一种特殊模型。考虑到流体润滑的存在，除上述两种模型外，还有一种摩擦模型，即流体摩擦模型。

1.1 静态摩擦模型

1.1.1 库伦摩擦模型

库伦摩擦模型的摩擦力的大小与负载正比，与接触面大小无关，方向与运动方向相反，其摩擦力的表达式如下[6]：

式中F为摩擦力，Fc为库仑摩擦力，v是相对滑动速度，sgn（v）是符号函数，当 v>0，sgn（v）=1，当v=0，sgn（v）=0，当 v<0，sgn（v）=-1。

1.1.2 库伦+粘性摩擦模型

当摩擦面之间存在液体且认为粘性摩擦力与速度成正比时，可将该模型描述为库伦+粘性摩擦模型，其摩擦力的表达式为[7]：

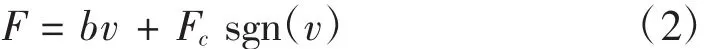
式中b是粘性摩擦系数，其余符号的含义同式（1）。

1.1.3 静摩擦+库仑+黏性摩擦模型

静摩擦+库仑+黏性摩擦模型是为了使摩擦模型能够描述静摩擦力，在库仑+黏性摩擦模型的基础上引入了静摩擦力，表达式为[7]：

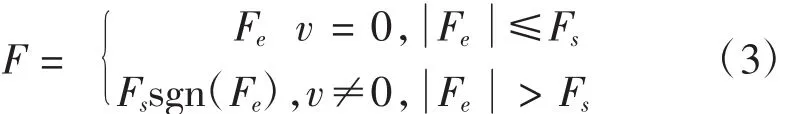
1.1.4 Stribeck摩擦模型

Stribeck摩擦模型是由Bo和Pavelescu于1982年通过一个指数模型来描述Stribeck现象的模型，其表达是为：

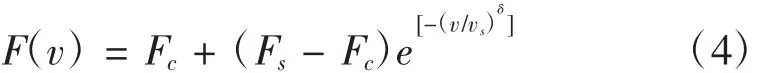
式中，vs是 Stribeck速度，vs和 δ是经验常数。Armstrong对该模型进行晚上后完善，添加了黏性摩擦项[8]，得出了如下的摩擦力表达式：

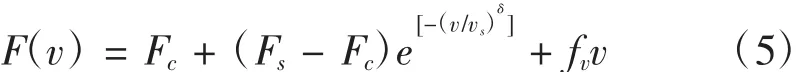
1.2 动态摩擦模型

1.2.1 Dahl摩擦模型

在外力的作用下，接触的法向、切向都是有柔性变形的。Dahl发现两相对运动在未达到最大静摩擦力之前，接触界面间会有微小的位移（即所谓预滑移位移），并用偏微分描述了摩擦力和位移的关系[10]，表达式为：

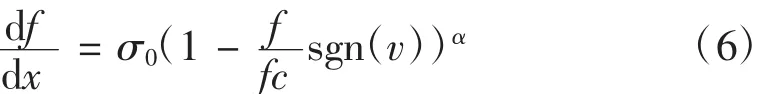
式中，f是摩擦力，x是变形量，σ0为刚度系数，v为相对运动速度，fc是库伦摩擦力，是与曲线形状有关的参数，图1为α＝1时的曲线形状。

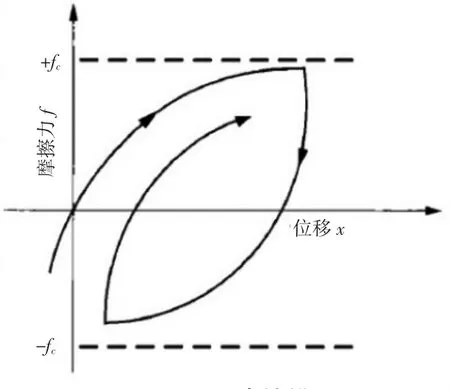
图1 Dahl摩擦模型

从时域角度看，上式可以描述为：

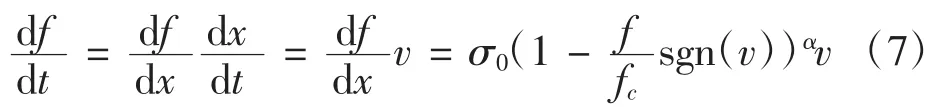
当α=1时，Dahl模型变为

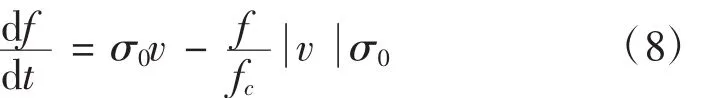
若设f=σ0z，则上式变为

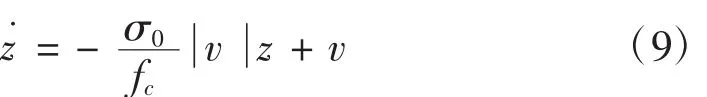
式中，z为鬃毛变形量，它是一个状态变量，代表的是在外力作用下的微小位移。稳态状况下，摩擦力为式：

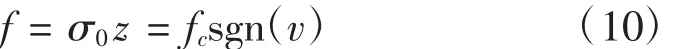
Dahl模型最大的特点是采用状态变量z来描述两接触副之间无数个接触峰的平均变形，是后续建立其它动态模型的基础。

1.2.2 LuGre摩擦模型

LuGre摩擦模型是由法国学者Canudas de Wit在Dahl模型的基础上综合了鬃毛模型的思想提出的，其模型示意图如图2所示。在该模型中，鬃毛的平均变形量用状态变量z来表示，摩擦力被认为是由鬃毛的挠曲变形产生[11]，其表达式为：

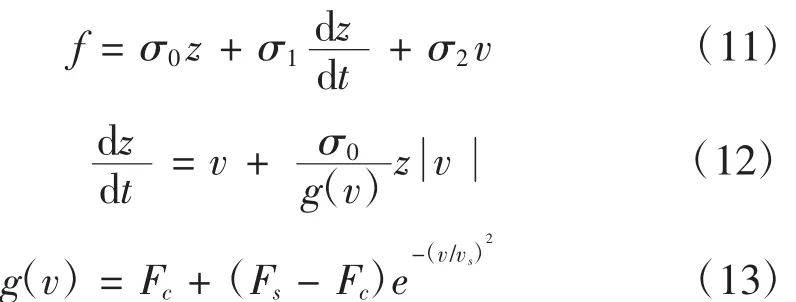
式中，f是摩擦力；σ0为鬃毛的刚度系数；σ1为阻尼系数；σ2为黏性摩擦系数；v为两表面相对速度；vs为Stribeck速度；Fc为库仑摩擦力；Fs为最大静摩擦力；函数g（v）描述的是Stribeck负斜率效应。

当 g（v）=Fc，σ1= σ2=0 时，LuGre 摩擦模型将简化为Dahl摩擦模型。若假设z˙=0，即鬃毛的平均变形处于稳态运动时，且忽略黏性。这样就可以得到前面所述的Stribeck摩擦模型。

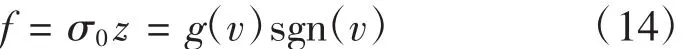
该模型应用一个一阶微分方程描述了库仑摩擦、可变静摩擦、黏性摩擦、预滑移位移、摩擦滞后和Stribeck摩擦等，属于连续模型，能够很好地体现真实的摩擦现象，并且各摩擦状态之间能够平滑地过渡，但最大的难点就是对其6个参数的辨识，尤其是对2个动态参数的辨识[12-15]。

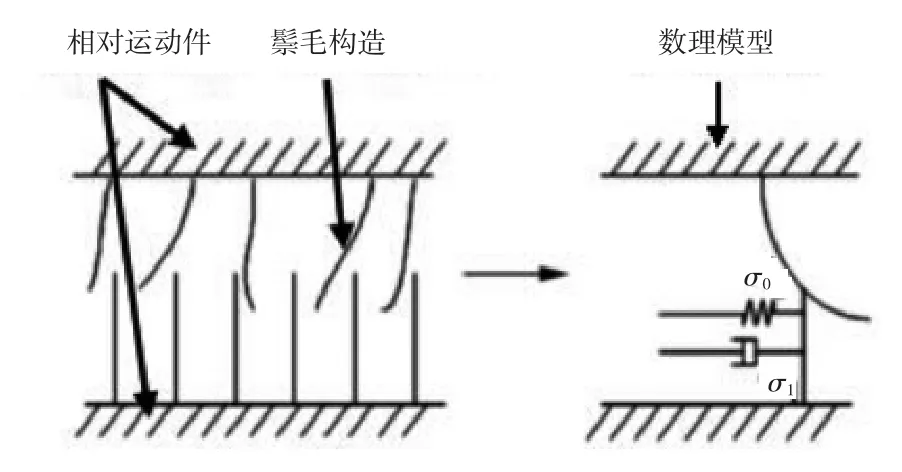
图2 LuGre摩擦模型

1.3 流体摩擦模型

1.3.1 牛顿内摩擦

牛顿内摩擦形成的摩擦力又称粘性力，是一种是组成液体分子的内聚力阻止分子相对运动而产生的内摩擦力，这种内摩擦力只能减慢液体流动，不能阻止液体流动，这是与固体摩擦力不同的[9]。牛顿内摩擦的模型示意图如图3所示，图中Ⅰ、Ⅱ是面积相等的两块的平板，两平板之间的距离很小并且其中充满流体，刚开始时，系统原先处于静止状态，之后平板Ⅱ不动，而平板Ⅰ以恒定速度v沿x方向上运动，在运动过程中，紧贴于平板Ⅰ下方的一薄层流体也以速度v随平板运动。当速度v不太大时，板间流体将形成稳定层流。从运动平板Ⅰ到固定平板Ⅱ的液体薄层的速度按某种曲线规律连续变化，靠近平板Ⅰ的液体比远离平板Ⅰ的液体具有较大的速度，并且离平板Ⅰ越远的薄层，其速度越小，至固定平板处，液体薄层的速度降为零。大量实验证明，牛顿内摩擦力大小与流体性质有关，与接触面积A和流体成正比，其表达为：

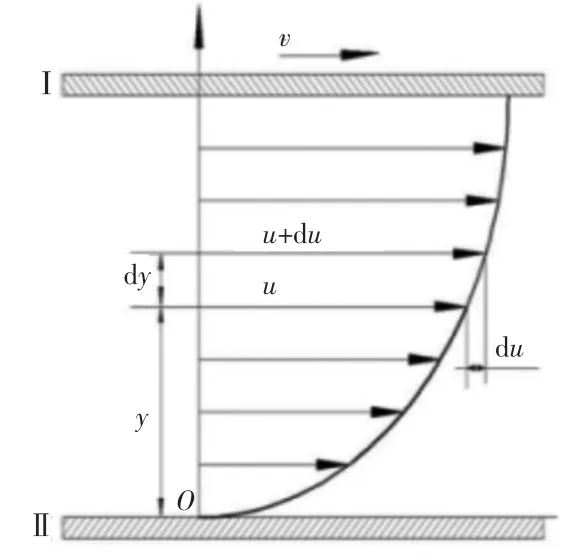
图3 牛顿内摩擦

1.3.2 流体动压润滑摩擦

流体动压润滑是由摩擦表面的几何形状和相对运动，并借助粘性流体的动力学产生动态压力来平衡外载荷一种模型，其示意图如图4所示。流体动压润滑的形成必须要满足一定的摩擦结构和相对运动速度条件：流体表面形成由大到小的收敛液（气）楔、流体表面具有一定的相对运动速度、流体要具备一定的粘度且供应量、外载小于总的液（气）膜力。在流体动压润滑条件下，两摩擦副表面之间被具有一定粘度的流体完全分开，此时固体之间的外摩擦被流体内摩擦替代，避免了固体表面的直接接触，在滑动过程中表面间的摩擦阻力得到了尽可能的减小，表面的损伤也得到了减低[16]。流体动压润滑的摩擦阻力极低，其摩擦系数在0.001～0.008或更低。流体动压润滑满足雷诺方程[17]，其普遍形式如下：

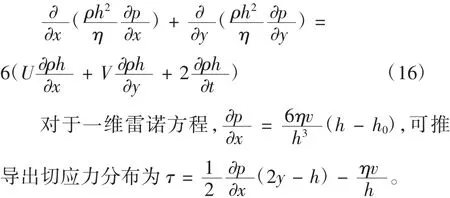
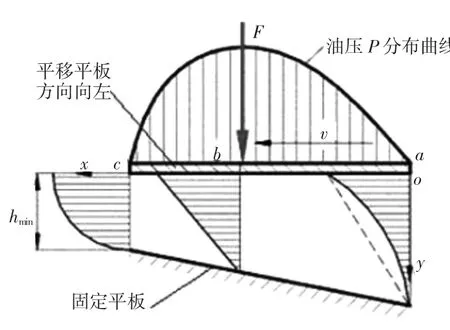
图4 流体动压润滑

1.3.3 弹性流体润滑摩擦

弹性流体润滑摩擦的模型如图5所示，两个摩擦传动的无限长滚子之间有油润滑，滚子半径分别为R1、R2。接触区的压力情况为赫兹接触压力分布，应力区的宽度为a。两滚子之间由于接触面的运动将润滑油带入高压接触区使得金属不直接接触。由于压力的升高，接触区内润滑油瞬间固化，两滚子间产生的速度差使在两滚子间的固化油膜产生剪切力[18]。在不同载荷、刚度、润滑油粘度下，有以下主要几种经验公式：

（1）当满足如下条件：①滚动体为刚性，不考虑其接触变形；②润滑油粘度为常数，不考虑粘度的影响；③滚动体为无限宽，不考虑润滑油在宽度方向上的流动，可利用马丁方程：

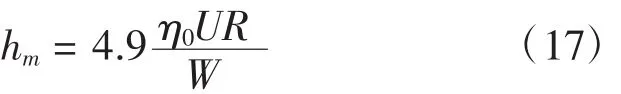
（2）当润滑油粘度受压力较大，且处于等温条件式，可利用布洛克方程：

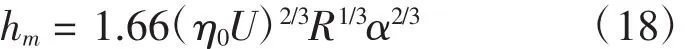
（3）当表面变形较大且润滑油粘度变化不大，可采用如下的布洛克方程：

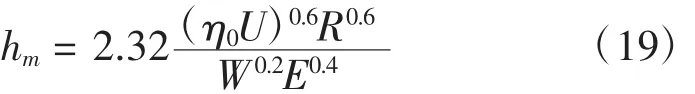
（4）但假设油不可压缩，无侧泄，忽略热效应式，可利用道森方程[19]：

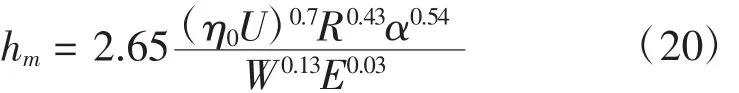
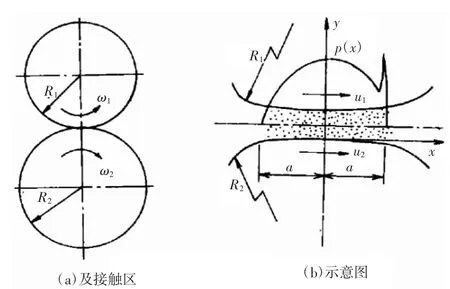
图5 弹性流体动力润滑

以上摩擦模型归结起来有静态摩擦模型、动态摩擦模型和流体润滑摩擦等，虽然三者都可以用于滚动活塞压缩机运动副的摩擦分析和计算，但只有对各运动副的摩擦状态充分了解后，选取合适的摩擦模型进行分析才能获得准确结论。

2 国内学者在压缩机各运动副摩擦状态和摩擦特性的研究

国内不同学者通过开展实验研究或者进行理论分析，对滚动活塞压缩机的摩擦磨损和摩擦特性展开了多方面的研究，直接或间接地指出了滚动活塞压缩机各运动副的摩擦状态。

张华俊等在《空调用滚动转子式压缩机动力分析》中[20]，指出偏心轴与气缸下盖、滚动活塞下表面、滑片与滑片槽、滑片端部与滚动活塞表面等处运动副为边界摩擦，其余运动副为流体润滑，并给出了各个运动副的摩擦功率计算公式。

樊灵等在《变频旋转式压缩机的研究现状与进展》中[21]，分析了旋转压缩机的动力学特性研究现状，指出叶片与滑槽间摩擦状态时边界摩擦，滚动活塞与气缸壁间是流体动压摩擦，滚动活塞受到了流体动压力和粘性剪切力。

马国远在《滚动活塞式压缩机的动力计算》中[22]，指出叶片与滑片槽运动副为边界摩擦，滚动活塞与气缸端盖间、滚动活塞与转子间、转子与气缸端盖间的摩擦为平行流体润滑，滚动活塞与气缸壁间为流体动压润滑，其不足之处是滚动活塞与转子间不能简化为平行流体润滑，而是符合流体动压润滑。

李爱国在《滚动转子式压缩机活塞异常磨损的研究》中[23]，指出滚动活塞与转子间、滚动活塞与气缸壁间的润滑状态更符合流体动压润滑，滚动活塞与气缸端盖间、转子与气缸端盖间的摩擦为平行流体润滑。

周杏标等在《旋转压缩机滑片端部动力学分析》中[24]，指出滑片与滑片槽间出现了边界摩擦，还存在粘滞摩擦。通过分析曲轴运转频率、滑片厚度、滑片端部半径、吸排气压差、活塞质量对活塞自转角速度、相对滑动速度、PcV值等的影响规律，有效预测滑片端部与活塞摩擦副的磨耗情况，并且提出减小PcV值方向，为旋转压缩机的优化设计提供指导思路。

周德馨在《提高旋转式压缩机可靠性的技术》中[25]，提出使用珠光体灰口铸铁等耐磨材料作为旋转压缩机的机芯材料，在磨合后其基体有所磨损后形成的沟槽有利于保持油膜，滑片在弹簧和排气压力推动下压向活塞，滑片端部R面与活塞外圆呈线形接触，运行中产生急剧的摩擦，容易出现大的磨损，且此处为边界摩擦。

董桂田在《滚动轴承摩擦力矩的弹性流体动压润滑计算》中[26]，指出在滚动轴承摩擦力矩计算中引入弹性流体动压润滑理论算得的结果与考虑润滑带来的摩擦、滚动摩擦和打滑经验式确定的值相差甚微，该文献提出的公式能准确计算滚动轴承任意时刻的摩擦力矩，揭示了滚动轴承摩擦力矩的弹性流体动压润滑计算的物理本质。

总结上述学者对滚动活塞压缩机的研究结论，可以大体明确滚动活塞压缩机各个运动副的摩擦状态：

（1）滚动活塞与滑片、滚动活塞与下端盖等处摩擦状态为边界摩擦；

（2）滑片与端盖、滚动活塞与上端盖等处摩擦状态为平行流体润滑摩擦状态；

（3）滑片与滑片槽间同时有边界摩擦和粘滞摩擦；

（4）滚动活塞与曲轴之间为流体动压润滑；

（5）滚动活塞与气缸间考虑为流体动压润滑或者弹流润滑。

3 作者在压缩机运动副摩擦的研究

在滚动活塞压缩机众多的运动副中，滑片与滑片槽运动副之间的状况变化最为激烈，因此，该运动副也是摩擦磨损的产生最为严重的地方，对压缩机的性能有着关键的影响。为了对滑片与滑片槽运动副之间的摩擦特性进行研究，且考虑到难以在压缩机本体上开展实验观测，作者在前期的研究中，设计一种与滚动活塞压缩机滑片与滑片槽运动副等效的实验装置，其示意图如图6所示。实验中，利用拉压力传感器测量试验装置的滑片与滑槽运动副之间的摩擦力，并借助高速摄影技术和图像处理技术分析滑片相对滑槽的运动状况，研究了滑片与滑槽运动副之间的摩擦特性[27]，结果表明滑片在运行期间具有明显的二阶运动特征，即滑片不仅存在沿着滑槽方向的来回运动而且存在左右偏摆运动，在工作周期内滑片始终保持顺时针倾斜姿态并规律性地发生横向运动与偏摆。滑片的二阶运动直接影响到滑片-滑槽运动副的油膜厚度，进而影响润滑状态，并且滑片两侧的润滑状态是动态变化的，在吸气腔侧，滑片与滑槽之间的润滑状态较为恶劣，主要表现为混合润滑和边界润滑，承载侧压力主要由流体动压和挤压组成；在压缩腔侧，滑片与滑槽之间的润滑状态较好，是完全流体润滑和较浅的混合润滑，承载侧压力主要为流体动压。

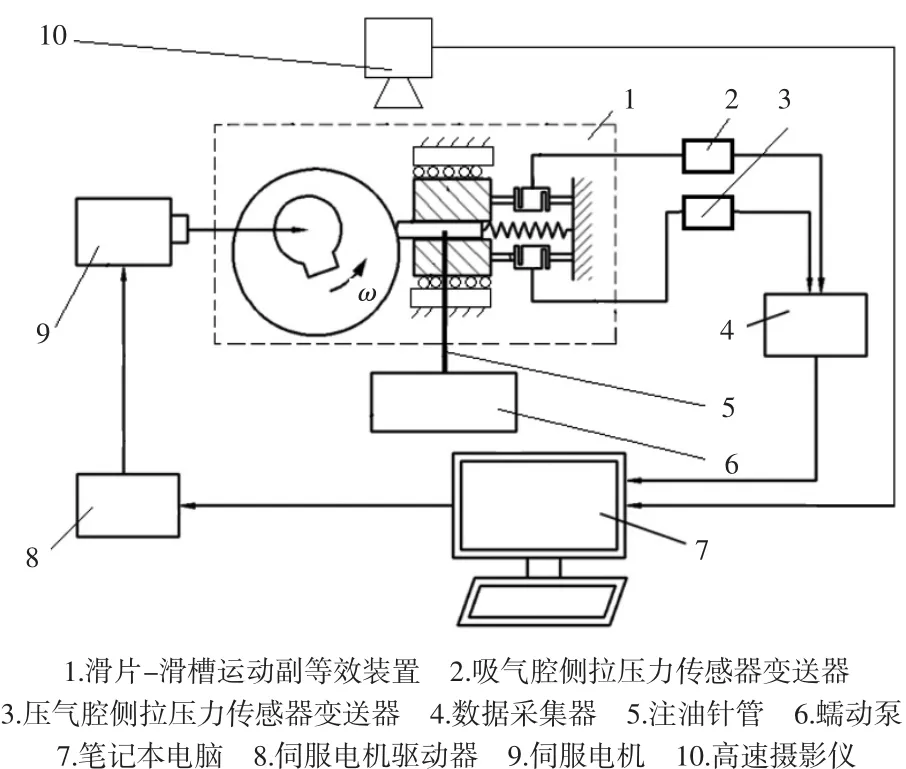
图6 滑片与滑片槽运动副的等效实验装置

4 总结

摩擦学自开展理论研究至今，经过国内外众多学者的研究、不断补充和完善，建立了形式多样、适合不同应用场景的多种摩擦模型，这些不仅包括将摩擦力描述为相对速度函数的静态摩擦模型，也包括将摩擦力描述为相对速度和位移函数的动态摩擦模型，另外，考虑到流体润滑的存在，除上述两种模型外，还有一种摩擦模型，即流体摩擦模型。这些模型下还有子模型，分别适用不同的应用场合和特定工况，从总体来看，已经足够丰富。而从中现有的摩擦学理论研究中获得的模型里面选用恰当的模型开展滚动活塞压缩机的摩擦特性研究，其关键在于要依据压缩机的实际运行工况进行选取。通过对近年来不同学者关于滚动活塞压缩机运动副摩擦模型建立和摩擦特性方面的研究进行综述，并结合作者的一些研究结论提出滚动活塞压缩机各运动副在摩擦模型建立和摩擦特性研究上的一些总结和展望如下：

（1）转子与下端盖、滚动活塞与滑片、滚动活塞与下端盖等运动副是边界润滑，宜采用库伦摩擦模型；

（2）滑片与端盖、转子与上端盖、滚动活塞与上端盖等运动副是平行流体润滑，宜采用平行流体牛顿内摩擦模型；

（3）滚动活塞与转子运动副是流体动压润滑，宜采用流体动压润滑摩擦模型；

（4）滚动活塞与气缸运动副为流体动压润滑或者弹流润滑，宜采用流体动压润滑摩擦模型或弹性流体动压润滑摩擦模型；

（5）滑片与滑片槽运动副之间的状况变化最为激烈，既有边界摩擦又有粘滞摩的运动副，很难用单一摩擦模型进行描述，并且滑片在运行期间具有明显的二阶运动特征，该二阶运动直接影响到滑片-滑槽运动副的油膜厚度，进而影响润滑状态，并且滑片两侧的润滑状态是动态变化的，在吸气腔侧，滑片与滑槽之间的润滑状态较为恶劣，主要表现为混合润滑和边界润滑，承载侧压力主要由流体动压和挤压组成；在压缩腔侧，滑片与滑槽之间的润滑状态较好，是完全流体润滑和较浅的混合润滑，承载侧压力主要为流体动压。对滑片与滑槽之间进行摩擦特性研究时，应考虑滑片二阶运动的影响。