女子竞技体操跳马运动学变量与裁判打分多元回归模型研究

汤仁圣，李 雪，何 卫

TANG Rensheng1，2，LI Xue3，HE Wei1*

0 前言

跳马是一项由助跑冲刺（约25 m）到踏板起跳，再到手撑上台，进而腾空并在空中完成一系列技术动作，最后在指定区域内稳定落地的竞技体操项目。国际体操联合会（2017）2017—2020评分规则（code of point，COP）规定，对所有国际体联比赛、世界锦标赛和奥运会，单项裁判组主要由D裁判组和E裁判构成，世锦赛和奥运会还会包括两名由国际体联主席委员会委派的参考裁判（R裁判）。跳马项目难度分（difficulty score，DS）由D裁判组根据评分规则中跳马动作的难度价值（difficulty value，DV）确定。在运动员接近踏板起跳后，E裁判组则从第一腾空阶段（双手撑马之前）、第二腾空阶段（从推马至落地站立）、撑马时身体姿势、偏离跳马延长轴、跳马整个动作技术完成和落地等方面，依照观察到的错误严重程度从10分开始，以0.1～0.5进行扣分。完成分（execution score，ES）是去掉一个最高分和一个最低分后，剩余裁判打分的平均值。最终得分（final score，FS）是难度分和完成分的总和。由此可以看出，E裁判组的打分主要是对跳马过程中运动员技术动作的运动学变量，如时间、角度和位移等运动学参数的视觉经验判断（国际体操联合会，2017；Aleksić-Veljković et al.，2016）。

有研究揭示跳马过程中的运动学变量如助跑速度、踏板速度、第一腾空时间、第二腾空时间、撑马时间等与跳马成绩难度分（Aleksić-Veljković et al.，2016）和完成分（白云庆，2015；Dillman et al.，1985）有密切关系。Atikovic（2012）研究的5个跳马表现预测模型中，第二腾空阶段模型是与难度分相关的最佳模型。Bradshaw等（2001）发现，助跑速度和第二腾空都与裁判打分相关，且增加助跑速度可能会增加毽子翻速度和踏板起跳速度。Dainis（1981）在研究中指出，在优秀女子竞技体操运动员中，助跑速度和踏板起跳速度的降低可能会影响腾空距离，但与起跳速度相比，助跑速度的减小会产生更大影响。Koh等（2007）研究指出，对于尤尔琴科动作，增加垂直起跳重心速度对于第二腾空高度和远度有显著影响。此外，下蹲跳腾空高度和下肢力量也与男子竞技体操难度分相关。一般来说，更快的助跑速度、更好的角速度转换、更短的撑马时间以及更长的第二腾空时间，都是运动员完成更高难度和更优质量技术动作的有利支撑条件，这其实也反映了跳马项目对运动员身体素质的内在本质要求。

以往跳马运动学变量和运动表现的相关研究或回归模型主要聚焦在具体的某个动作技术或个人技术优化上，存在采用简单的回归统计方法分析复杂的相互关联变量、样本规模小或缺乏真实比赛成绩等不足（Aleksić-Veljković et al.，2016；Heinen et al.，2012；Hiley et al.2015；Jackson et al.，2011；King et al.，2005；Koh et al.，2007）。一项基于1995年世界体操锦标赛男子跳马数据进行的裁判评分模型研究中，其最优模型负责解释27%～57%的差异（Takei et al.，2000）。低到中等准度的预判模型不足以对日常训练、比赛或监控等提供实际指导意义。此外，国际体操联合会（Fédération Internationale de Gymnastique）规定体操项目竞赛规则每届奥运会后（每4年1次）进行相应修改及修订。因此，以往的研究在实际应用中存在一定局限性。本研究以2017年全国体操锦标赛女子跳马比赛数据为对象，利用偏最小二乘法对跳马运动学变量、难度分和官方比赛成绩进行回归分析，以期建立新周期体操评分规则下女子跳马预判评分模型，并评估预判评分模型的可靠性和准确性。

1 研究方法

1.1 数据采集

本研究数据为2017年全国体操锦标赛女子跳马资格赛组I（前手翻类型）、组II（第1腾空转体90°或180°）的比赛视频。通过高速摄像机（JVC PX100）采集运动员助跑倒3步至落地过程的影像学数据，摄像机拍摄频率100 fps，主光轴与助跑跑道垂直，距离跑道约50 m。在助跑跑道边沿（近跳马端）水平方向间隔1 m放置5个标记点，在跳马器械支柱面对摄像机方向沿垂直方向间隔0.25 m放置3个标记点。本次比赛采用国际体操联合会最新2017—2020年女子竞技体操评分规则。

1.2 数据解析

本研究共获得48个有效女子跳马动作样本。通过有经验编码人员（Cronbach's alphar=0.96）采用Dartfish二维视频分析软件解析获得每个样本运动学变量。运动学变量被划分为3个阶段：1）助跑阶段，包括倒3步、倒2步、倒1步和起跳至跳板（图1）的时间、位移和速度及助跑速度等13个运动学变量；2）第一腾空阶段，包括在板时间、撑马时间和撑马与在板时间比等3个变量；3）第二腾空阶段，包括最大腾空高度、最大腾空高度时间和第二腾空时间等3个变量，共计19个。运动学变量名称、编码和说明详见表1。

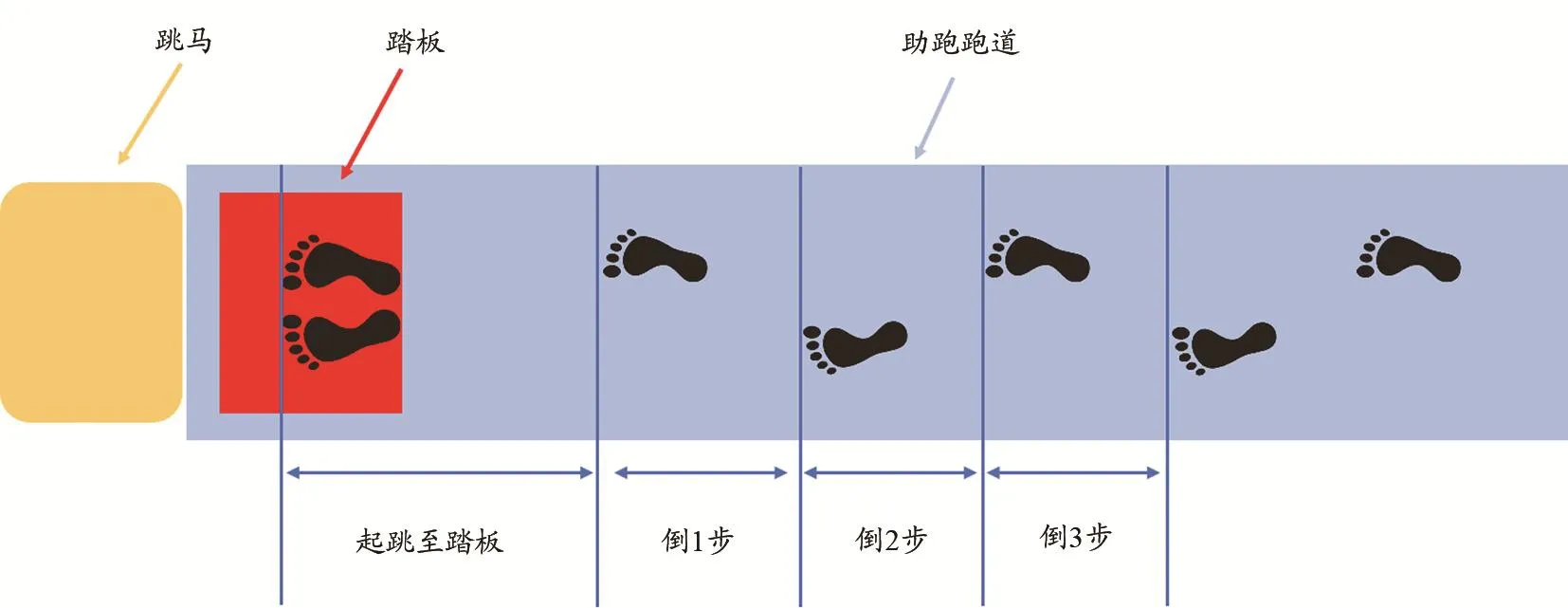
图1 第一阶段倒3步、倒2步、倒1步和起跳至踏板分解示意图Figure 1. Schematic of 3rd-Last Step，2nd-Last Step，1st-Last Step and Take-off to Springboard in the Approach Phase

表1 二维运动学指标名称、编码及说明Table 1 Name，Code and Description of Two--Dimensional Kinematic Parameters

1.3 偏最小二乘法回归分析

本研究中采用偏最小二乘法进行回归建模分析（partial least squares regression，PLSR）。偏最小二乘法是一种新型多元统计分析方法，主要用于多因变量（包含单一变量）对多自变量的回归建模，特别是对自变量存在严重多重相关性的条件下，发现自变量中最能预测因变量的潜在变量。该方法集回归建模（多元线性回归）、数据结构简化（主成分分析）以及两组变量之间的相关性分析（典型相关分析）等基本功能于一体，回归建模分析的结论更加可靠，整体性更强（王惠文等，2006）。

偏最小二乘法回归建模过程如下：设有单因变量y和p个自变量{x1，x2，…，xp}，观测n个样本点，构成自变量和因变量的数据表X=[x1，x2，…，xp]n×p，和Y=[y]n×1。偏最小二乘法回归分别在X和Y中提取成分t1和u1，提取成分需满足下面两个要求：1）t1和u1应尽可能多的携带他们各自数据表X和Y中的变异信息；2）t1和u1的相关程度达到最大。这两个要求表明，t1和u1应尽可能好的代表数据表X和Y，同时自变量的成分t1对因变量的成分u1又有最强的解释能力。在第1个成分t1和u1被提取后，分别实施X对t1的回归和Y对t1的回归。如果回归方程已经达到满意精度，则算法终止。否则，将利用X被t1解释后的残余信息以及Y被t1解释后的残余信息进行第2轮的成分提取。如此往复，直到能达到满意的精度为止。若最终对X共提取了m个成分t1，t2，…，tm，偏最小二乘回归将通过实施y对t1，t2，…，tm的回归，然后在表达成y关于原变量x1，x2，…，xp的回归方程，至此，偏最小二乘回归建模完成。

本研究中因变量y是官方最终得分，20个自变量x包括一个官方的难度分和解析获得的19个运动学变量。将所获得的样本（n=48）随机分为两部分，对第1部分（n1=43）数据使用偏最小二乘法建立跳马预判评分模型，并采用全交叉验证法对预判评分模型进行验证（王惠文等，2006；Dainis，1981）。第2部分（n2=5）对预判模型可靠性进行检验。本研究中运用Hotelling's T2方法筛选异常值。P值设为0.05。

2 研究结果与分析

2.1 PLSR模型

对第1部分数据使用偏最小二乘法进行预判评分模型建立和交叉验证。解释方差接近于100%作为本研究中偏最小二乘法成分选取的标准。图2所示为使用第1部分数据进行偏最小二乘回归建模不同成分的解释方差和验证解释方差，图3所示为建模和验证过程预判得分与参考裁判得分（真实比赛得分）回归结果。可以看出第2轮成分提取结束，偏最小二乘建模的解释方差R2cal=86.24%，模型验证解释方差R2val=82.83%，此后趋于平稳。全交叉验证过程因为样本数每次去掉一个，所以验证的解释方差比模型的解释方差略小。在模型的校准和验证中，预测的Y（FS）和参考Y（FS）之间的关系显著（rcal=0.929，rval=0.910），均方根误差（root mean square error，RMSE）分别为0.305 6和0.349 5。该统计结果表明校准数据拟合度较高，模型可以用于描述数据集。因此在本研究中，选择前2个成分用于建立跳马预判评分模型，PLSR方程如下：

2.2 相关性分析

2.2.1 裁判评分变量与预判模型的相关性分析

由表2可知，成分1中解释方差的自变量X和因变量Y分别为56%，75%和成分2分别为15%，11%。跳马最终得分与成分1存在显著强相关（r=0.867，P＜0.01）与成分2显著弱相关（r=0.333，P＜0.01）；难度分与成分1存在显著强相关（r=0.888，P＜0.01）与成分2呈显著中度相关（r=0.488，P＜0.01）。

图2 女子体操跳马预判评分PLSR建模（实线）和验证（虚线）解释方差图Figure 2. Explained Modelling（solid line）and Validation（dotled line）Variances Diagram by Using PLSR

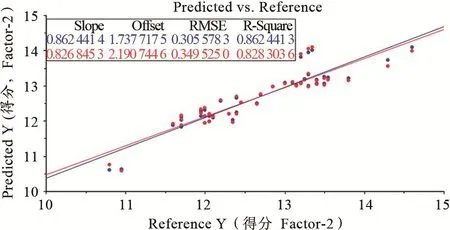
图3 预判评分与参考裁判得分回归图Figure 3. Regression Diagram of Prediction Score and Reference Score

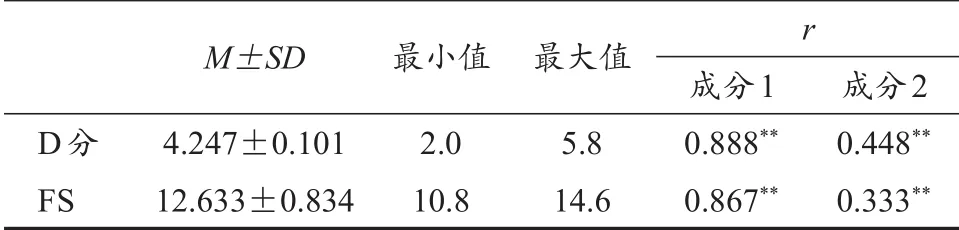
表2 裁判评分变量与预判模型的相关性分析Table 2 CorrelationalAnalyses of Official Judges Score Variables with the Prediction Model

2.2.2 助跑阶段变量与预判模型的相关性分析

由表3可知，助跑阶段的时间变量中，成分1与倒2步时间存在统计学意义上的显著弱相关（r=-0.387，P＜0.01），与起跳至踏板时间存在呈显著中度相关（r=0.400，P＜0.05）；倒2步时间与成分2之间呈较弱的相关性（r=-0.348，P＜0.05）。从助跑阶段的位移变量来看，成分1与倒3步位移（r=0.352，P＜0.05）、倒1步位移（r=0.338，P＜0.05）之间存在显著弱相关性，与起跳至踏板位移呈显著中度相关（r=0.447，P＜0.05）；成分2与倒3步位移呈显著中度相关（r=-0.404，P＜0.01）、倒2步位移呈显著弱相关（r=-0.364，P＜0.01）。从助跑阶段的速度变量来看，成分1与倒3步速度（r=0.702，P＜0.01）、倒2步速度（r=0.638，P＜0.01）、倒1步速度（r=0.624，P＜0.01）呈显著中度相关，与助跑速度（r=0.840，P＜0.01）和起跳至踏板速度（r=0.810，P＜0.01）呈显著高度相关性；成分2与助跑速度（r=-0.358，P＜0.01）和起跳至踏板速度（r=-0.397，P＜0.05）呈显著弱相关。

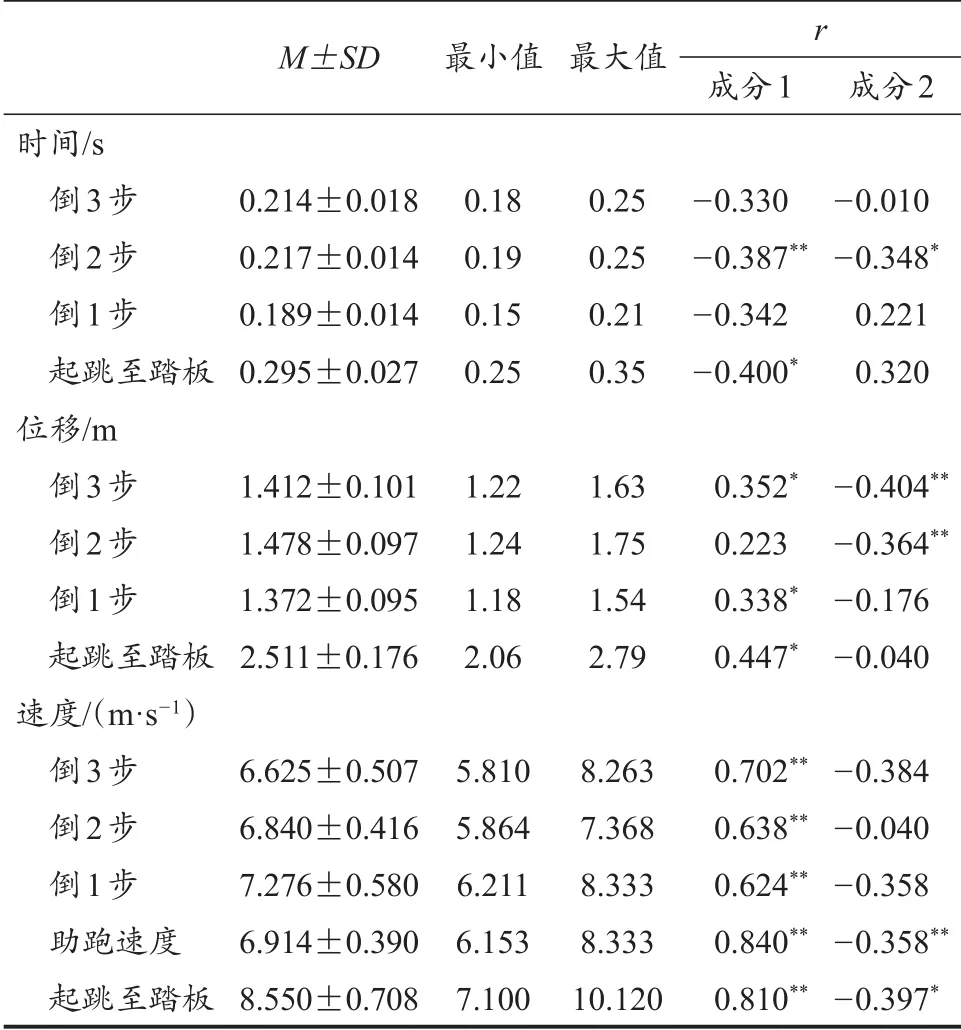
表3 助跑阶段变量与预测模型的相关性分析Table 3 Correlational Analyses between the Run-up Stage Variables with the Prediction Model

2.2.3 第一腾空阶段变量与预判模型的相关性分析

根据表4结果可知：成分1与撑马时间（r=-0.712，P＜0.01）、撑马与在板时间比（r=-0.459，P＜0.05）有统计学中等程度的显著相关性。

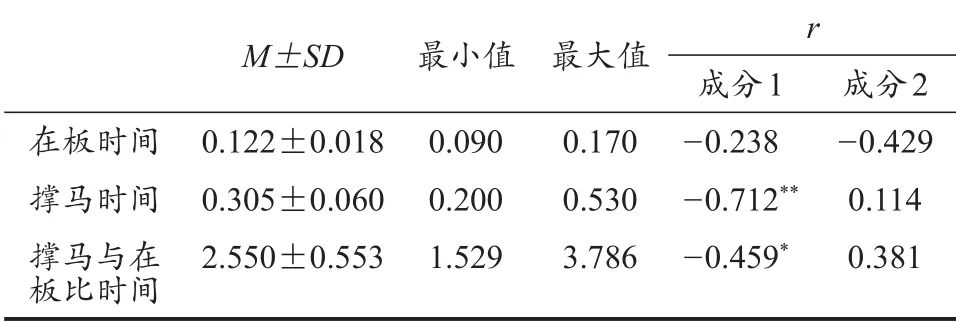
表4 第一腾空阶段与预判模型的相关性分析Table 4 CorrelationalAnalyses of the First Flight Duration with the Prediction Model /s

2.2.4 第二腾空阶段变量与预判模型的相关性分析

由表5可以看出，成分1与最高腾空时间有中度显著性相关（r=0.521，P＜0.05），与第二腾空时间高度显著性相关（r=0.891，P＜0.05）。

2.2.5 数据集之间相关性分析

本研究用椭圆图绘制成分1和成分2中的X和Y数据集之间的相关关系（图4）。外椭圆表示相关系数r=1，内椭圆表示相关系数r=0.5，两变量间距离越接近，代表两个变量之间的相关关系也就越强（r的绝对值也就越大）。同一象限内的变量之间呈正相关关系，不同象限的变量之间呈负相关关系。根据图4可知，D分与第二腾空时间和最终得分呈高度正相关；倒3步速度、倒2步速度和倒1步速度呈高度互相关；然而速度变量、距离变量与时域变量呈负相关关系。椭圆内的变量难度分、第二腾空时间、倒2步速度、助跑速度、踏板接触时间、倒2步时间和撑马时间等是本研究中PLSR模型的重要变量。

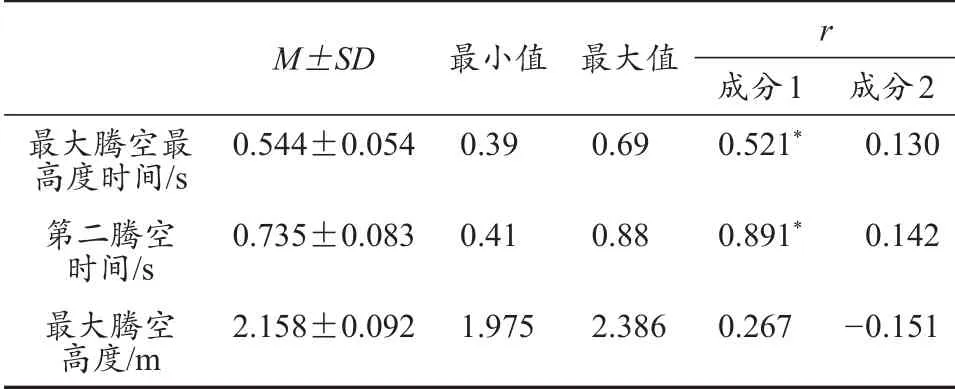
表5 第二腾空阶段与预判模型的相关性分析Table 5 CorrelationalAnalyses of Second Flight Duration with the Prediction Model

本研究对助跑速度、撑马时间、第二腾空时间与D分之间的相互关系进行进一步研究发现：1）在跳马助跑过程中助跑速度越快，支撑手在跳马器上的支撑时间越短，第二腾空时间越长；2）跳马的难度系数越大，则需要助跑速度越快，撑马时间越短，第二腾空时间越长；3）当大多数运动员难度分在4.6～5.8分之间时，助跑速度需大于7 m·s-1、撑马时间小于0.3 s，第二腾空时间则在0.75 s以上（图5）。

2.3 跳马预判评分模型检验

使用第2部分5个样本数据对建立的跳马预判评分模型进行检验（图6）。通过计算，预测的最终得分偏差分布在0.233～0.519，满足体操评分规则的可接受范围（Gervais，1994）。使用本研究建立的跳马预判评分模型，4个样本（80%）的预测得分在偏差范围内，与真实比赛成绩接近，说明，本研究基于偏最小二乘法建立的跳马预判评分模型有较高的可靠性和准确性。

3 讨论

本研究结果表明基于二维视频分析获得的运动学参数和已知的动作难度价值，可以使用偏最小二乘法建立跳马预判评分模型，并能准确预判跳马运动表现得分。本研究包含19个运动学参数和D分的预判评分模型能较好地解释差异因素，并有80%的准确性和可靠性。难度分、第二腾空时间、倒2步速度、助跑速度、踏板接触时间、倒2步时间和撑马时间是预判评分模型的主要变量，这也与之前的研究结果相似（Bradshaw et al.，2001；Takei etal.，2000）。此外，本研究中第二腾空时间与最大腾空高度与其他研究中优秀女运动员数据相似，但撑马时间和第二腾空时间与优秀男子跳马运动员相比较差（Dillman et al.，1985；Takei et al.，2000）。本研究数据结果表明，速度变量能更好地描述运动员第二腾空前的跳马运动表现，而时间变量可以更好地描述第二腾空后的跳马运动表现。

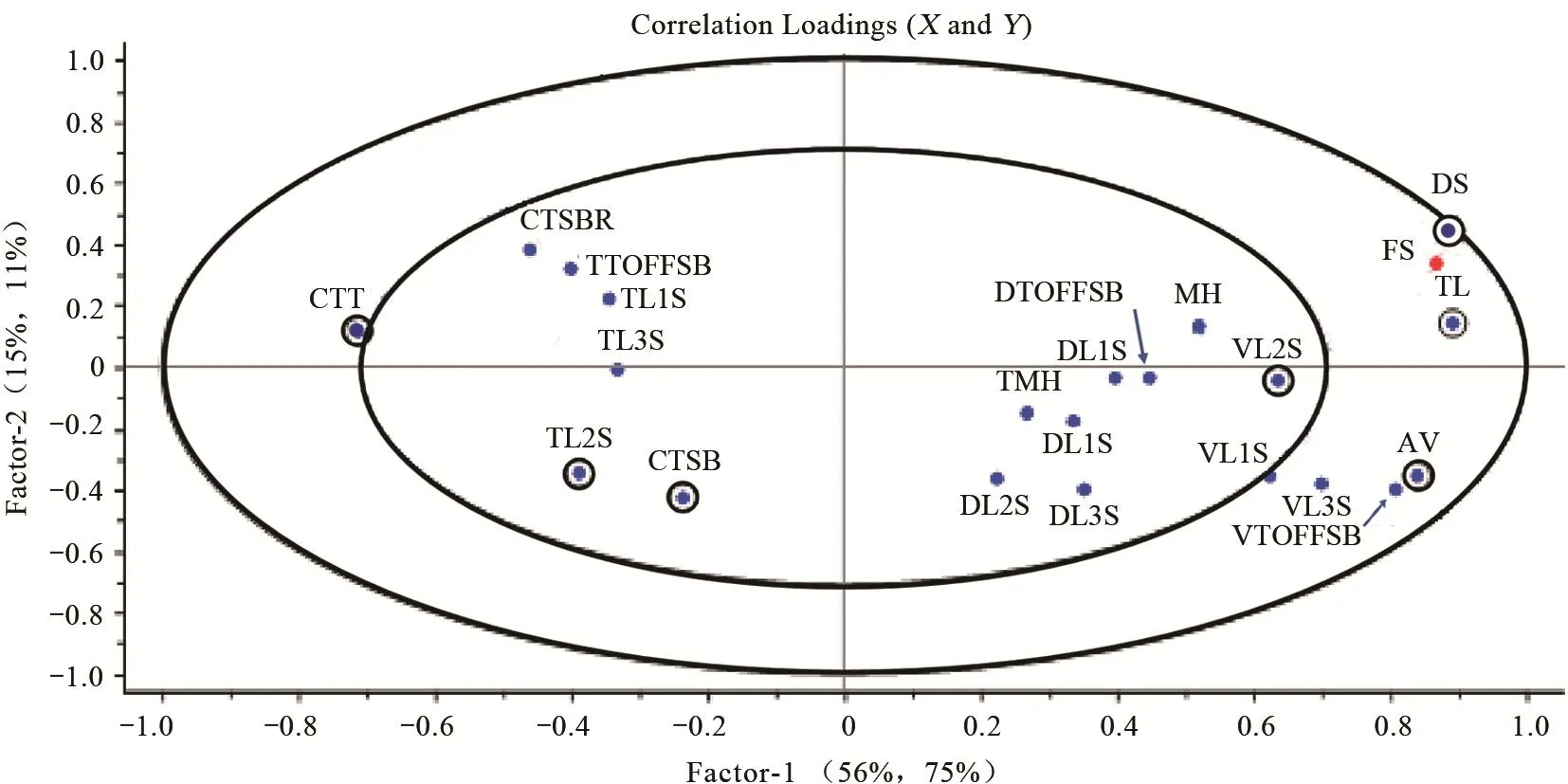
图4 PLSR预判评分模型成分1和成分2中X和Y数据集相关图Figure 4. Correlation Diagram of X and Y in Factor 1and Factor 2 of PLSR Prediction Model

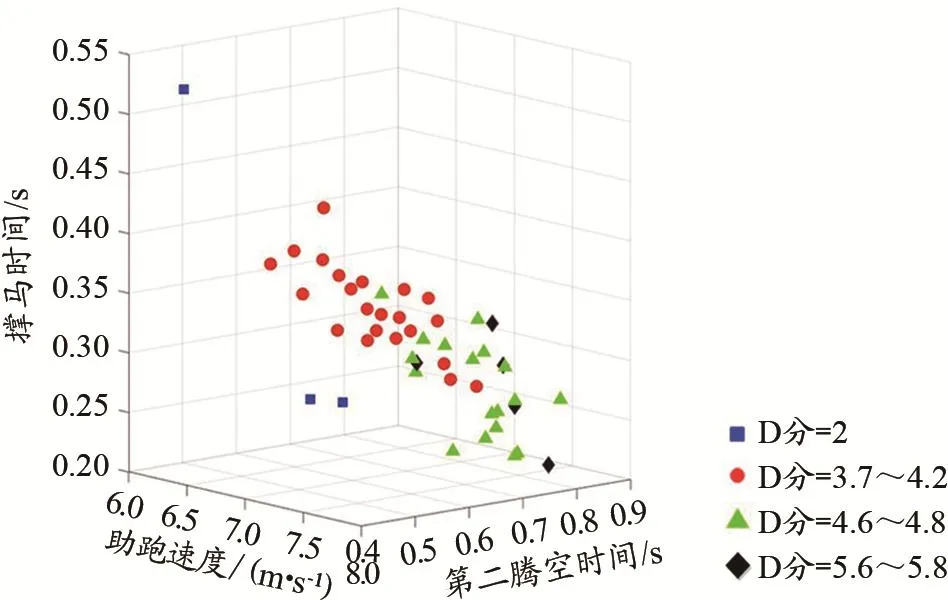
图5 助跑跑速、撑马时间、第二腾空时间与D分三维散点图Figure 5. 3D Scatter Diagram for Run-up Velocity，Vaulting Support Duration，Second Flight Duration Time，and Difficulty Score

以往研究表明，在竞技体操跳马中，助跑跑速是一个非常关键的运动学指标，助跑跑速越快，为第一腾空阶段和第二腾空阶段提供动力就越大（Hiley et al.，2015；Takei et al.，2000）。本研究也发现，随着难度分的提高，女子体操运动员助跑速度也随之提高。4.6的难度分和约7.0 m·s-1的助跑速度为分水岭，小于4.6难度分有较慢的助跑速度，而大于4.6难度分的跳马动作需要更快的助跑速度。国际竞技体操跳马大赛中，难度分水平均在5.8以上（白云庆，2015；江芸等，2017），如果运动员采用较高的难度动作，较慢的助跑速度可能会增加体操运动员损伤风险（Takei et al.，2000）。2017年全国体操锦标赛中，女子跳马整体难度不高，完成分平均低于8.4分，由此可见，我国女子体操运动员在跳马运动项目中很难胜任高难度的技术动作，这也从侧面反映出我国女子体操运动员体能素质方面的缺乏。因此，教练应注意进一步探究提高助跑速度的方法，同时注重提高女子体操跳马运动员的体能素质，将有助于提高我国跳马难度水平和完成质量（江芸等，2017）。

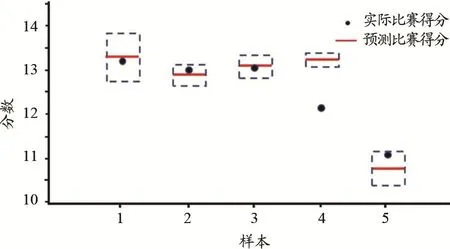
图6 预判评分模型验证Figure 6. Validation of Prediction Scoring Model

跳马第二次腾空阶段动作完成质量与其上一阶段完成效果密切相关。有研究报导撑马时间越短，在第二腾空获得的高度势能和动力冲量越大（吴成亮等，2015；Bradshaw et al.，2010；Gervais，1994）。本研究数据结果显示，撑马时间越短，则第二腾空时间就越长。以难度分4.6为分界点，随着难度分的逐渐提升，撑马时间少于0.3 s，而第二腾空时间大于0.7 s。该结果表明，撑马时间越短而第二腾空时间越长，越能为完成高难度动作和提高技术动作完成质量奠定基础。本研究中，本次比赛我国女子体操运动员撑马时间平均在0.3 s，而澳大利亚优秀女子体操运动员撑马时间约0.10～0.14 s，我国女子体操运动员第二腾空时间约0.7 s，短于澳大利亚优秀女子运动员 0.8 s（Bradshaw et al.，2001，2009）。这可能是多技术因素共同导致的结果，如手触马时的角度、踏板接触时上肢动作、比赛中的心理压力等（Koh et al.，2007），这些因素将影响后续腾空阶段运动学变量和跳马完成质量。尽管第二腾空高度不是本研究预判评分模型的主要因素，但我国女子跳马体操运动员第二腾空高度普遍不高。

4 备战东京奥运会的启示

当前奥运备战过程中，各项目越来越重视体能训练工作，国家体操队也不断加强基础体能训练和专项体能素质训练。竞技体操运动表现与体能有相关性，但提高体能不一定提高运动表现，需要有针对性的体能训练才能提高运动表现。同时，随着体能的提升，体操运动员的专项技术也需要适应才可能达到最终提高运动表现的目的。下一步，我们将纳入更多难度范围和更高完成质量的跳马动作，不断完善跳马预判评分模型。随队的科研人员可以借助该预判模型分析，为优秀体操运动员和教练员判断运动表现存在的薄弱环节，并为训练方向、技术优化、提高训练效率、降低伤病风险等提供建议。随着深度学习、动作识别等技术的发展，跳马运动学数据获取会更加快速准确，跳马预判评分模型有可能是未来科学化训练研究的重点，也有可能成为数据化科学训练的主要工具。

5 结论

通过二维视频分析获得的体操跳马运动学变量和已知难度分，可以建立裁判打分的预测模型，而不需要详细的技术输入。本研究采用的技术动作为前手翻类型，难度分范围为2.0～5.8分，因此在应用该模型时需满足这些条件。