坐标测量机测头系统的校准研究*

陈伟琪 陈艳华 张勇

坐标测量机测头系统的校准研究*

陈伟琪1陈艳华2张勇1

（1.广东省现代几何与力学计量技术重点实验室 2.清华大学)

介绍坐标测量机测头性能参数的校准和补偿方法；设计一套基于三维微宏移动平台和测力传感器的校准系统；采用该系统对坐标测量机模拟式测头的触发变形进行实验研究，获得测头的探测力和实际变形量；补偿后的测头系统在平面内探测标准测量球的误差不超过0.3 μm，满足坐标测量机模拟式测头的校准需求。

接触测头；标定；预行程

0　引言

测头系统是三坐标测量机的核心部分，通常分为接触式测头与非接触式测头2类。其中接触式测头又分为机械式测头、触发测头和扫描测头[1]；非接触式测头主要指光学测头。目前，由于光学测头景深方向的量程较小，主要用于二维测量，在三维测量中接触式测头占主要地位。三坐标测量机的测头误差是测量误差的主要来源。接触式测头的预行程、重复性、分辨力、量程、测量力大小和自身耦合等性能是影响测量精度的主要因素。因此，对测头误差进行辨识并补偿，是提高三坐标测量机测量精度的有效手段[2-3]。

测头性能参数辨识和误差补偿也称为测头标定，可分为离线标定和联机标定。联机标定是在三坐标测量机上，使用标准器件（标准球）对测头进行校准。离线标定需要用特定的标定系统对其进行实验分析、检测并校正。目前，测头标定主要是联机标定，但联机标定事实上是三坐标测量机的整机标定，其标定结果包含测量机机械结构、控制系统和测量软件的误差。为单独获得测头系统探测补偿数据，本文设计一套基于微动台PI-611.3SF和测力传感器Nano17-Net/DAQ的校准系统，以实现测头的离线标定。

1　校准系统原理

标定装置示意图和结构图分别如图1、图2所示，主要由基座（花岗岩）、测力传感器Nano17-Net/DAQ（量程为/-12 N，-17 N，分辨力为1/320 N）、微动台PI-611.3SF（//三轴量程为100 μm×100 μm×100 μm，分辨力为1 nm）、三维微宏位移平台和监视窗口CCD组成。

图1　标定装置示意图

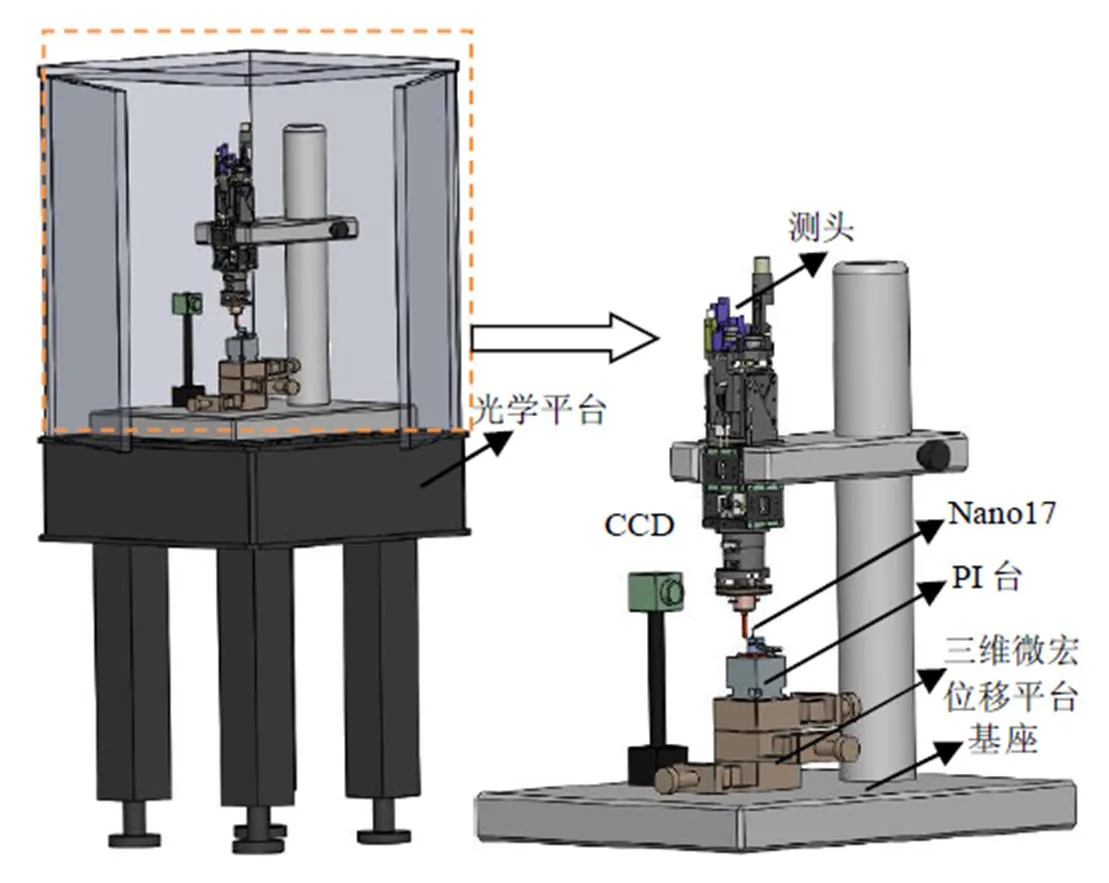
图2　标定装置结构图

本文标定的测头为三层双片簧正交层叠式模拟测头，标定的性能参数有测头三轴的耦合误差、测量力和预行程。标定过程中，三维微宏位移平台提供大行程位移，使PI台工作面与测头测端慢慢靠近直至接触；PI台固定于三维微宏位移平台上方，提供精密的微小位移量；Nano17用于标定触发力的大小。信号处理系统负责传感器输出电压信号的采集、转换和传输。上位机进行最后数据处理、分析和曲线描述，并建立位移量与测头信号之间的关系曲线，实现测头性能的测试和校准。实验期间，需时刻观察监视窗口CCD，避免因位移过量导致测头损坏。

1.1　测量力

接触式测头依据受力—变形的原理进行测量，测量力是其一项重要指标[4-5]。测量力过大会降低测量精度甚至破坏被测件；测量力过小则接触不可靠，同样影响测量精度。本装置采用测力传感器Nano17来标定测量力，并以此计算测杆变形和挤压变形。

影响测量结果的测杆变形和接触面的挤压变形如图3所示。测量外尺寸情况下，测头的实际位移量1´总比测杆不变形情况下的位移量1小；测量内尺寸情况下，测头的实际位移量2´总比测杆不变形情况下的位移量2大；测杆变形需引入测端直径修正量1、减小两倍的测杆变形2及挤压变形量2W。

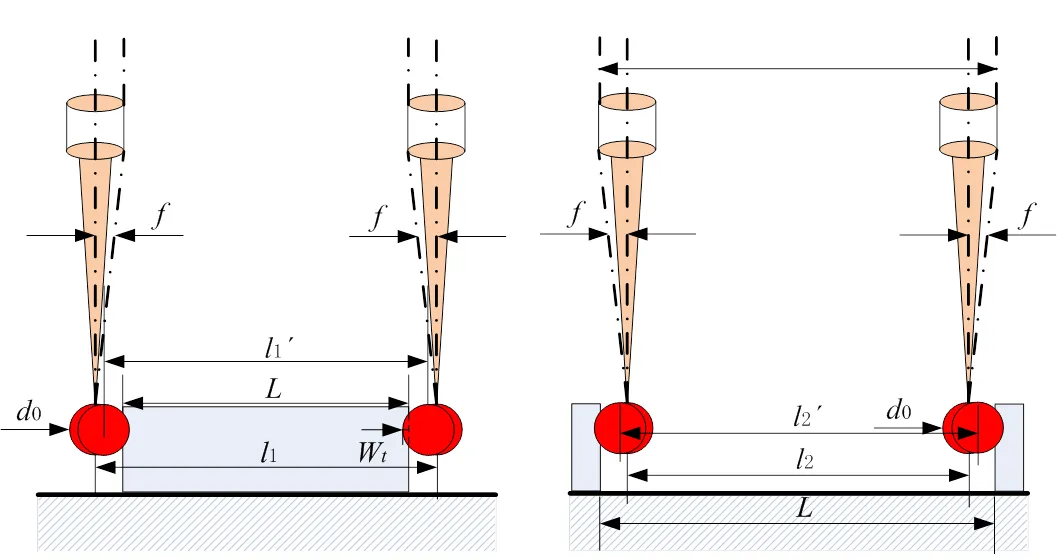
图3　测量真实外尺寸与内尺寸

测端直径修正量1为

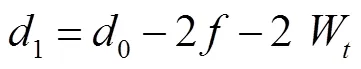
其中0为测头直径。

测杆弯曲位移变形量[6]为

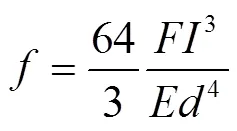
其中，为测量力；为测杆长度；为测杆材料的弹性模量；为测杆直径。

当测球接触被测面时，在测量力作用下，测球的弹性变形W[7]为

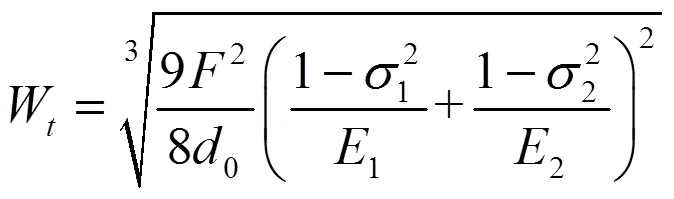
其中，为测量力；1，2分别为测球和被测面的弹性模量；1，2分别为测球和被测面的泊松比；0为测头直径。

测量外尺寸时，被测尺寸为

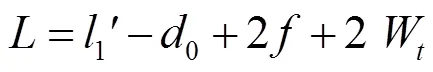
测量内尺寸时，被测尺寸为

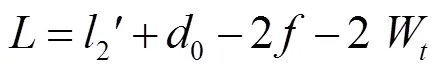
1.2　预行程

测量过程中有2个关键点：接触点P和触发点Q，如图4所示。工件开始接触测针时，由于测杆系统并非理想刚体，不会立即产生触发信号，而是在其变形足够大时才会有信号输出。因此，在PI台驱动工作面移动从与测头接触被测体到测头发出触发信号之间有一段位移，这段位移称作为预行程。

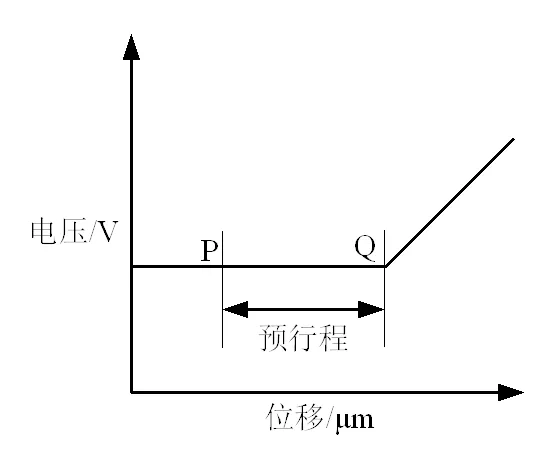
图4　预行程示意图

测头预行程计入测量结果会影响测量精度，且由于测头结构特性，沿各方向的测头预行程是不同的，表现为测头预行程的空间变化。预行程变化给误差补偿带来困难，降低了接触式测头在精密曲面（如圆度、圆球度和齿轮齿廓偏差等）测量的精度应用[8-10]。因此，触发式测头在使用前必须标定其预行程并进行补偿，本文采用实际变形量进行综合补偿。

2　实验与结果

基于搭建的实验台，针对测头触发力及测针变形、预行程进行实验验证和分析。

标定触发力流程如图5所示。在测头信号值达到阈值时，Nano17输出值即为触发力。

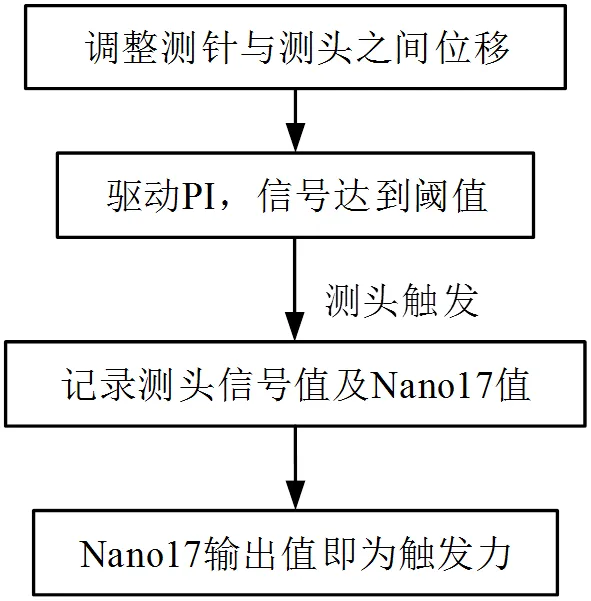
图5　触发力流程图

按照图5流程进行实验：调整三维微宏位移平台，使得安装测力传感器的工作平台接近测头测端；控制PI台微动接触测头测端，继续驱动PI台，直到测头输出值达到阈值；记录此时Nano17输出信号，此输出力值即为触发力；上述步骤重复10次，计算平均值。

本文采用海克斯康系列测头，理论触发力为（0.10±0.03）N，测杆长度40 mm、测头直径为3.5 mm，测头与PI台工作面的材料参数如表1所示。实验时分别改变测杆直径，测量方向的测量力和实际变形量。测头的理论变形量按式(6)计算。测头实验数据如表2所示。

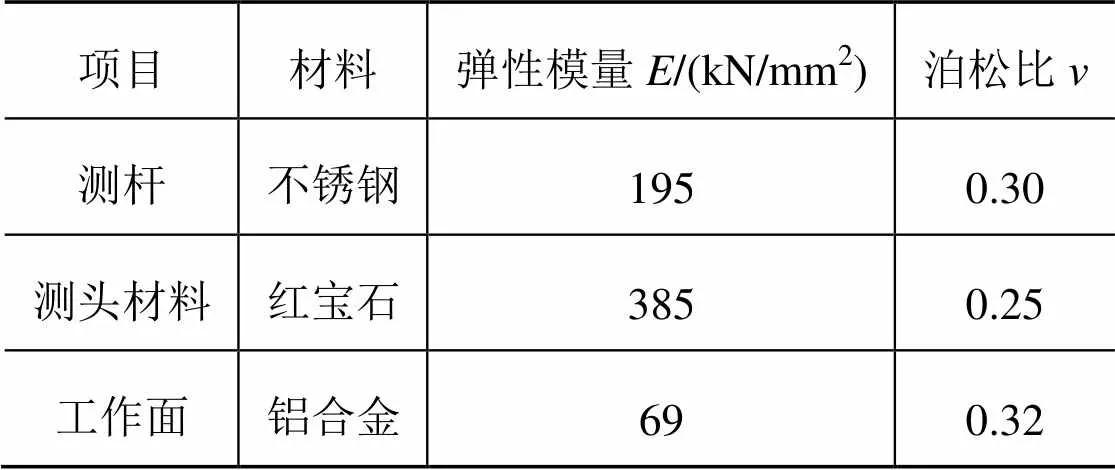
表1　测头参数和工作面材料参数

将表1参数分别代入式(2)和式(3)，可得

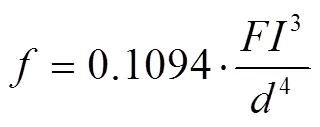
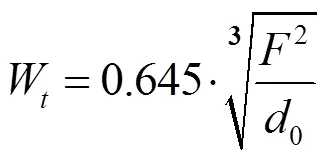
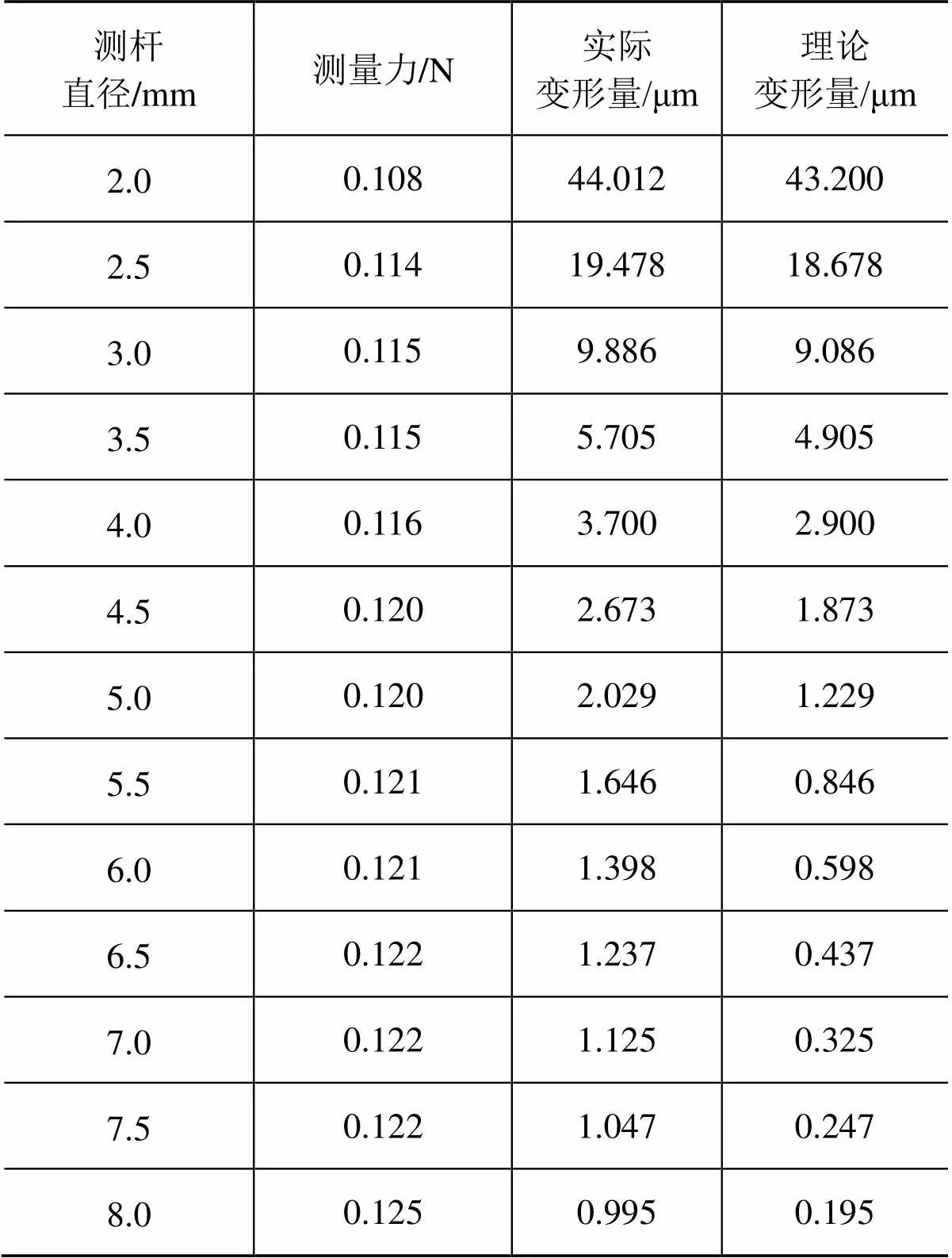
表2　测头实验数据

当测杆直径从2.0 mm~8.0 mm变化时，方向测杆的实际变形量范围为44.012 μm~0.995 μm。经与理论变形量相比，实际测量的变形量约大0.805 μm，这是由于探测系统的测头预行程、机械装置的摩擦以及挤压变形量影响所致。方向的测头补偿按该校准系统给出的实际量值进行补偿。

采用该装置测量探头方向的测量力和实际挤压变形量。当测杆直径从2.0 mm~8.0 mm变化时，对应的测头直径2.5 mm ~15.0 mm，测得的实际测量力处于0.120 N~0.128 N，实际挤压变形量处于1.016 μm~ 0.960 μm，取测量力为0.120 N，按式(7)计算得到理论挤压变形量为0.120 μm~0.061 μm。与方向同样的道理，方向实际变形量比理论值约大0.898 μm。方向的测头补偿也按该校准系统给出的实际量值进行补偿。

3　验证与分析

根据以上实验数据，对广泛使用的直径为5 mm的测头进行补偿验证实验。方向测头综合变形补偿值取2.029 μm，方向测头综合变形补偿值取0.988 μm。采用三维微宏位移平台与标准测量球进行验证。为提高三维微宏动位移的准确性，平面内的位移采用激光干涉仪来监控。激光干涉仪的允许误差为±（0.03 μm+1.5×10-6，为测量距离）。本次验证采用的标准测量球直径为29.9063 mm，扩展不确定度= 0.4 μm (= 2)，已采用精密测长仪和圆度仪校准；5 mm测头也采用精密测长仪校准，实际直径值为4.9983 mm,扩展不确定度= 0.3 μm (= 2)。

在三维微宏位移平台上固定安装标准测量球，精密调整测头测球与标准测量球的相对位置。在方向探测时，确保测头测球的球心处于标准测量球方向的最大直径所在平面上；在方向探测时，确保测头测球的球心处于标准测量球最高点的正上方。

采用该5 mm测头在平面内探测标准测量球，从激光干涉仪上获得测量结果为34.9003 mm，方向测头综合变形补偿值取2.0290 μm，修正后测头直径取4.9943 mm，得到探头探测标准测量球的直径为29.9060 mm。影响该直径的不确定分量有：1）激光干涉仪存在±0.1 μm的测量误差，按均匀分布，则引入的不确定分量为0.06 μm；2）测头直径校准引入的不确定度分量为0.15 μm；3）按经验，获取最大直径的拐点存在0.1 μm不确定分量，合成以上3项不确定度分量，取= 2，则探测标准测量球直径的扩展不确定度为0.4 μm。

三维微宏位移平台上方向无法安装激光干涉仪来提高宏动位移的准确度，故目前方向的补偿数据还无法获得验证。

4　结论

本文采用基于三维微宏位移平台和测力传感器的校准系统，对测头系统的探头进行了实验研究，可获得测头系统的测量力、在平面及方向的探测补偿值。与标准测量球比对表明，该校准系统在平面内能可靠获取探测补偿数据。由于坐标测量机的测头系统空间数据转化关系比较复杂，不同坐标系统的耦合精度有待加深研究，方向的探测补偿值还有待进一步的实验验证。

[1] 张国雄.三坐标测量机[M].天津:天津大学出版社,1999.

[2] Cai Zewei, Liu Xiaoli, Peng Xiang, et al. Phase error compensation methods for high-accuracy profile measurement[J]. Meas. Sci. Technol, 2016,27 (4): 045201.

[3] Mehrdad Givi, Mayer JRR. Validation of volumetric error compensation for a five-axis machine using surface mismatch producing tests and on-machine touch probing [J]. Elsevier Science, 2014(87):89-95.

[4] 韩翠娥,籍凤荣,米双山,等.接触触发式测头触发力的理论分析[J].军械工程学院学报,2005,17(5):75-79.

[5] 丁邦宙,费业泰,夏豪杰,等.三维触发式坐标测量机测头误差分析与性能实验[J].农业机械学报,2011,42(11):228-231.

[6] Rong Liang, Otto Jusko, Frank Ludicke ,et al. A novel piezo vibration platform for probe dynamic performance calibration[J]. Meas. Sci. Technol, 2001(12):1509-1514.

[7] H. Aoyama, M. Kawai, T. Kishinami. A New Method for Detecting the Contact Point between a Touch Probe and a Surface[J]. Annals of the CIRP, 1989, 38(1):517-520.

[8] 程方,范光照,费业泰.纳米三坐标测量机接触式测头预行程测量[J].纳米技术与精密工程,2010,8(2):109-113.

[9] 高峰,赵柏涵,李艳,等.基于误差隔离的触发式测头预行程标定方法[J].仪器仪表学报,2013,34(7):1581-1586.

[10] Yang Q, Butler C, Baird P. Error compensation of touch trigger probes[J].Elsevier Science, 1996, 18(1):47-57.

Research on the Calibrating of CMM Probe System

Chen Weiqi1Chen Yanhua2Zhang Yong1

(1.Guangdong Provincial Key Laboratory of Modern Geometric and Mechanical Metrology Technology 2.Tsinghua University)

A calibration system based on a three-dimensional micro-macro mobile platform and force sensor to calibrate an analogue touch probe is proposed in this paper. The detection force and actual deformation of the probe are obtained. The compensated probe system is verified by the standard measuring ball, and the detection error of the compensated probe does not exceed 0.3 μ m. The device meets the calibration requirements of three-dimensional analog probe.

Touch Probe; Calibration; Pre-Travelling

NQI专项高端装备制造质量大尺度计量测试方法与技术研究（2017YFF0204800）

陈伟琪，男，1973年生，硕士，高级工程师，主要研究方向：精密几何量计量检定和研究。E-mail: cwq0579@163.com