一种求解单调包含问题的惯性混合邻近外梯度算法

何明明, 彭建文

(重庆师范大学数学科学学院,重庆401331)

1 引言

对于单调包含问题, 即: 找到x∗∈X 使得

其中B:X ⇒X 是极大单调算子, X 是实Hilbert 空间.凸优化问题, 平衡问题和单调变分不等式等许多问题都可以归结为单调包含问题(1.1).单调包含问题在图像处理和聚类等实际问题中有着广泛的应用[1].

邻近点算法是解单调包含问题的一类经典算法, 它由Martinet[2]提出, Rockafellar[3]进一步发展而成.其迭代格式为

其中正则参数λk>0,Id是单位算子.Alvarez 和Attouch 于2001 年在文献[4]中提出解含有单调算子的广义方程的惯性邻近点算法, 并证明了该算法的弱收敛性.

混合邻近外梯度算法是由Solodov 和Svaiter[5]在1999 年针对单调包含问题提出的另一类算法.即

初始化任取初始点x0∈X, 任意给定令k=1.

步骤1选择容差参数并找到yk,vk∈X,εk≥0 使其满足

步骤2执行一个外梯度步:xk+1=xk−λkvk.令k:=k+1, 返回步骤1.

实质上, 混合邻近外梯度算法是邻近点算法的一种不精确版本, 在每一次迭代中, 对应的近似子问题都应在一个相对误差准则内求解, 这与Rockafellar 提出的邻近点算法的可加误差准则不同.混合邻近外梯度算法的另一个特点是它还允许通过文献[6]中提出的极大单调算子的ε-enlargement 来松弛单调算子.

混合邻近外梯度算法作为设计新方法和分析现有方法的复杂性的框架特别有用.例如Monteiro 和Svaiter[7]在2013 年提出块状分解混合邻近外梯度算法, 并证明了该算法的迭代复杂性, 且在该算法的框架下证明了交替方向乘子法的遍历迭代复杂度; Goncalves, Melo 和Monteiro[8]在2017 年提出一种新的正则化混合邻近外梯度算法, 并建立了该算法的迭代复杂性, 且证明了交替方向乘子法的变体是该算法的特殊实例; Alves 和Svaiter[9]在2016 年提出了一种新的求解强单调包含问题的混合邻近外梯度算法:

初始化任取初始点x0∈X, 任意给定σ∈[0,1),k=1.

步骤1选定0<λk≤λk−1, 并找到yk,vk∈X,εk≥0, 使得

步骤2计算xk:

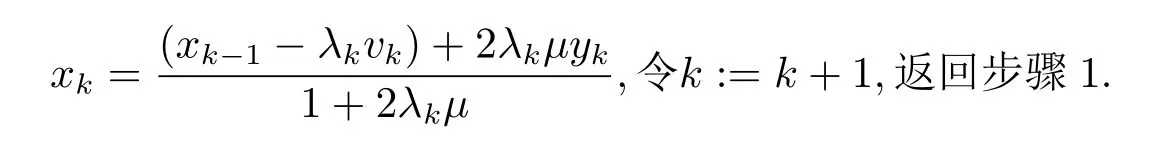
并用混合邻近外梯度算法的框架证明了Korpelevich 外梯度算法的迭代复杂性.

近年来, 惯性邻近点类算法被大量用于设计和分析各种具有惯性的一阶邻近算法.例如Chen[10]等人提出求解具有可分结构的线性约束凸优化问题的惯性交替方向乘子法, 并建立了渐近收敛率和非渐近收敛率; Bot, Csetnek 和Hendrich 在文献[11]中提出了求解单调包含问题的惯性Douglas-Rachford 分裂算法, 并证明了该算法在希尔伯特空间中的收敛性;Bot 和Csetnek[12]在2015 年提出求解单调包含问题的惯性混合邻近外梯度算法, 并建立了该算法的弱收敛性和渐近收敛性; Alves 和Marcavillaca 于2018 年在文献[1]中提出一种求解单调包含问题的新的惯性混合邻近外梯度算法, 并得到了它的渐近收敛率和非渐近全局收敛率.

受上述文献的启发, 本文提出了一种新的求解单调包含问题的惯性混合邻近外梯度算法,并得到了它的收敛性和非渐近全局收敛率.不同的是, 本文中的惯性系数的范围得到了扩大,其系数区间为特别的, 当µ=0 时, 惯性区间为[0,1], 正好与文献[12]中的区间一致.

本文结构如下: 首先是预备知识, 对概念和符号进行说明, 并对证明过程中所需的定理进行说明; 然后是本文的主要内容, 本文提出了一种用于求解单调包含问题的惯性混合邻近外梯度算法, 并证明了它的非渐近全局收敛率.最后本文提出了惯性混合邻近外梯度算法的两种特殊情况: 求解含有Lipschitz 连续算子的强单调包含问题的惯性Tseng’s 向前向后算法,并建立了该算法的弱收敛性和非渐近全局收敛率; 求解含有强单调算子和Lipschitz 连续算子的原始―对偶问题的惯性非精确Spingarn’s 部分逆算法, 并得到了该算法的弱收敛性和非渐近全局收敛率.

2 预备知识

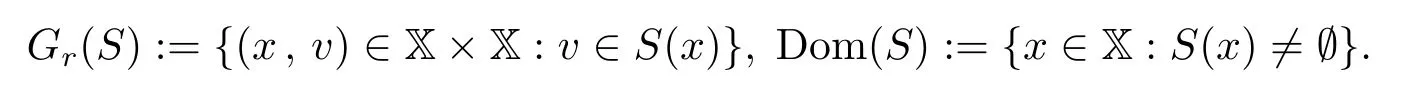
若S−1(v)={x:v∈S(x)}, 则称S−1:X ⇒X 是集值算子S的逆.

本文主要研究单调包含问题的求解算法, 即含有(极大) 单调算子的包含问题.在本节接下来的内容中将回顾一些基本概念和结论.

定义2.1[12]若集值算子A:X ⇒X 满足

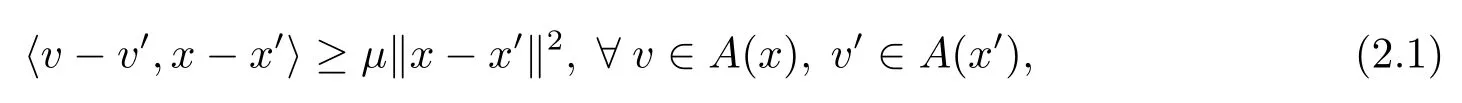
则称算子A是µ-强单调的.特别地, 如果µ=0 则称A是单调的.

定义2.2[12]设算子A:X ⇒X 是单调的, 如果不存在其他单调算子B真包含于A, 则称算子A是极大单调的.即如果单调算子B:X ⇒X 满足Gr(A)⊂Gr(B), 则A=B.

集值算子S,:X ⇒X 的和S+:X ⇒X 定义为

显然, 如果A:X ⇒X 是µ-强单调算子,B:X ⇒X 是单调算子, 则A+B也是µ-强单调算子.特别的, 两个单调算子的和也是单调算子.

定义2.3[6]设算子T:X ⇒X 是极大单调的, 如果T[ε]:X ⇒X 满足

则称算子T[ε]是极大单调算子T的ε-enlargement.

注意到T⊂T[ε],∀x∈X.从而可以将T[ε]视为T的外延或近似.下面是关于T[ε]的性质的结论.

命题2.1[13]令T,S:X ⇒X 是集值映射, 则下列论述成立

(i) 如果ε≤则

(iii)T是单调算子当且仅当T(x)⊆T0(x).

(iv)T是极大单调算子当且仅当T(x)=T0(x).

(v) 如果T是极大单调算子,点列{(yk,vk,εk)}使得对于任意的k≥1 有vk∈T[εk](yk),点列{yk} 弱收敛于点x, 点列{vk} 收敛于点v和点列{εk} 收敛于点ε, 则v∈T[ε](x).

定理2.2[12](Opial 定理)令若对于任意的x∗∈Ω 和X 中的数列{xk} 使得存在.如果{xk} 的每个弱聚点都属于Ω, 则数列{xk} 弱收敛到Ω 中的点.

引理2.3[14]令c,d∈X,p∈R, 则

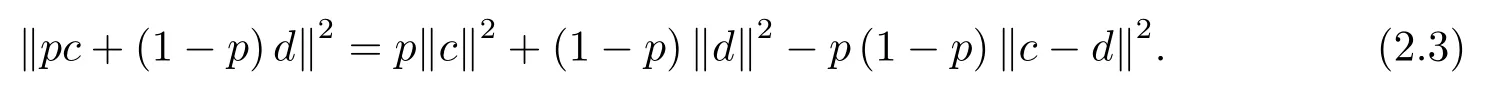
3 惯性混合邻近外梯度算法

一般来说, 问题(1.1) 多半是不适定的, 而对于含有强单调算子的单调包含问题总是适定的.因此在实际应用中, 通过正则化将问题(1.1) 近似为强单调包含问题, 这一技术可追溯到Tikhonov[15]的工作中.下面考虑强单调包含问题

其中A:X ⇒X 是极大µ-强单调算子,B:X ⇒X 是极大单调算子.假设问题(3.1) 有解.

下面给出求解问题(3.1) 的惯性混合邻近外梯度算法.

算法1

步骤0任取初始点x0=x−1∈X, 任意给定α∈[0,1),α0∈[0,α],σ∈[0,1),k=1;

步骤1选定αk∈[αk−1,α], 计算

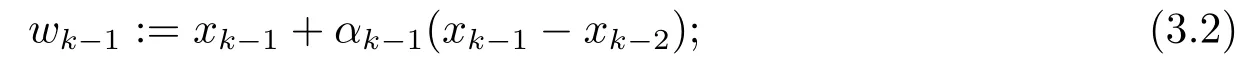
步骤2选定0<λk≤λk−1, 并找到yk,vk∈X,εk≥0, 使得

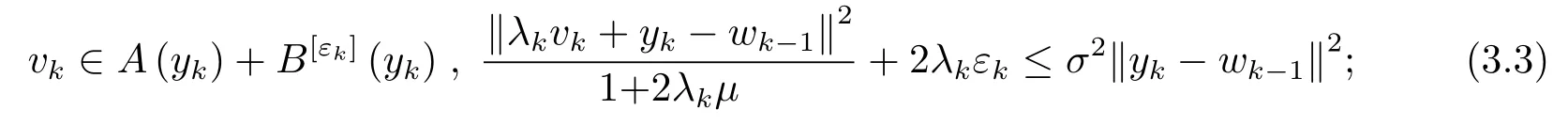
步骤3计算xk

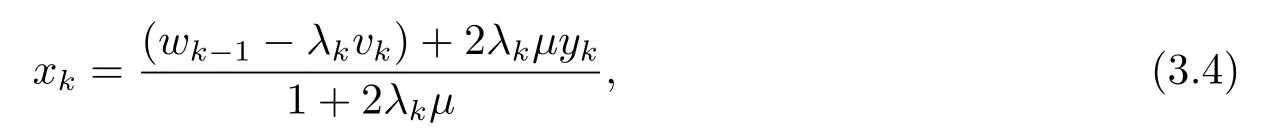
令k:=k+1, 返回步骤1.

注3.1(i) 对单调包含问题(1.1) 进行正则化处理

其中µ>0,x0是初始点.令A(x)=µ(x−x0), 则算子A是极大µ-强单调算子.此时问题(3.5) 是问题(3.1) 的特殊情况.A是µ-强单调算子, 根据Minty 定理[16]可知它的解集是单点集, 记是它的解, 即∈(µ−1B+Id)−1(x0).当µ接近于0 时, 它近似于问题(1.1)的解.

(ii) 针对问题(3.1) 也可以用文献[12]中的惯性混合邻近外梯度算法, 此时惯性系数的范围从[0,1[; 而算法1 通过正则化的技巧将惯性系数的范围从[0,1]扩大为加快了迭代速度.

(iii) 当αk≡0 时, 算法1 退化为文献[9]中的求解问题(3.1) 的算法1.

(iv) 当µ=0 且αk≡0 时, 算法1 退化为文献[5]中的求解问题(1.1) 的混合邻近外梯度算法.

(v) 当αk≡0 且σk≡0 时,xk−1=wk−1由(3.3) 式可知εk≡0 和xk−1−λkvk=yk,从而由(3.4) 式可知xk=yk=xk−1−λkvk.此时, 算法1 退化为经典的邻近点算法[3].

(vi) 当σk≡0 时, 算法1 退化为文献[4]中的惯性邻近点算法.

引理3.1令点列{xk}, {yk}, {wk}, {αk}由算法1 生成, 取x∈X, 则∀k≥1, 有

证由(3.2) 式可得wk−1−x=(1+αk−1)(xk−1−x)−αk−1(xk−2−x).将p=αk−1,c=xk−2−x,d=xk−1−x代入(2.3) 式, 即得(3.6) 式.

命题3.2令点列{xk}, {yk}, {wk} 由算法1 生成, 则∀x∗∈(A+B)−1(0), 有

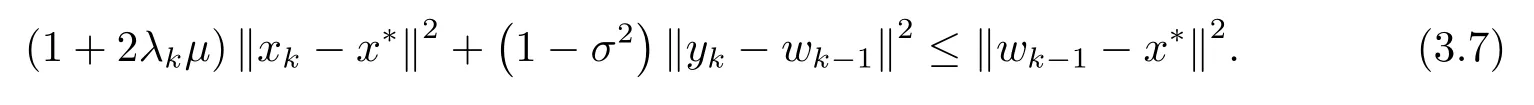
证由(3.4) 式可知wk−1=(1+2λkµ)xk−2λkµyk+λkvk, 事实上,∀a,b,c∈X, 有从而可知

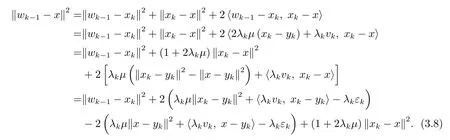
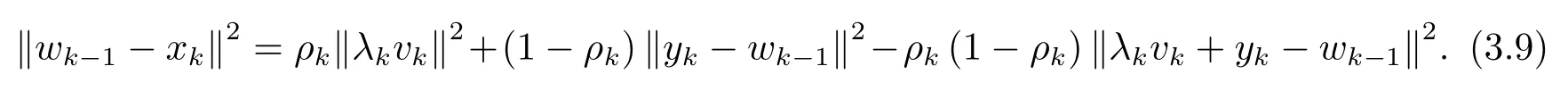
由(3.4) 式可知

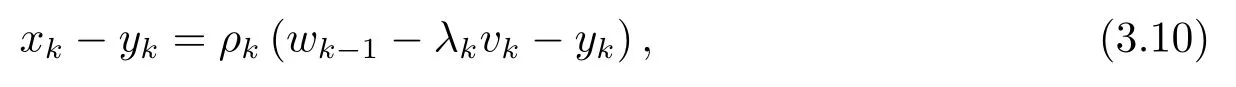
从而由(3.10) 式有

事实上, (1 −ρk)=2λkµρk, 从而由(3.10) 式可得

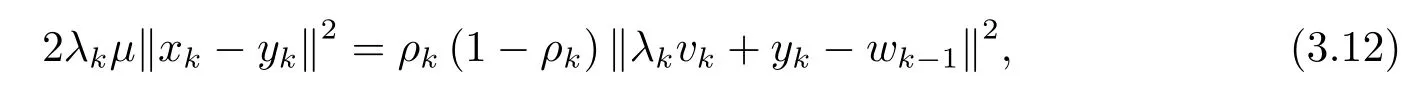
由(3.9), (3.11) 和(3.12) 式可得

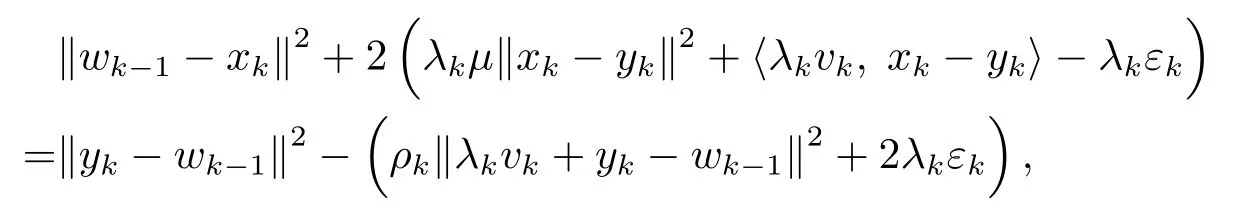
并联立(3.3) 和(3.8) 式可得

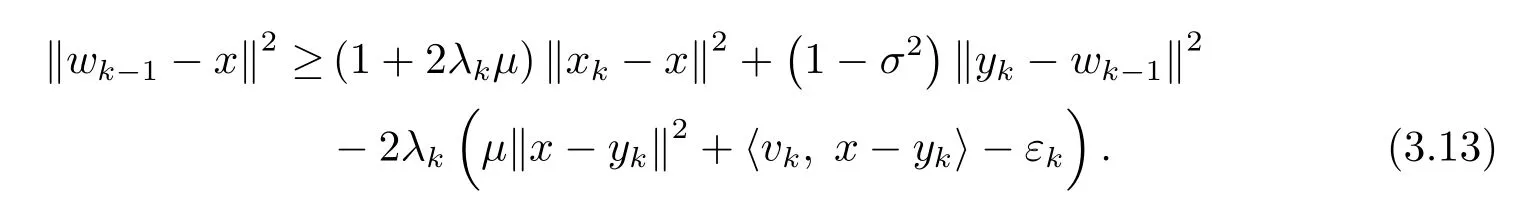
若∀x∗∈(A+B)−1(0), 则存在a∗∈A(x∗), −a∗∈B[εk](x∗).由(3.3) 式可知: 存在ak∈A(yk),bk∈B[εk](yk), 使得vk=ak+bk.由(2.1) 与(2.2) 式可知

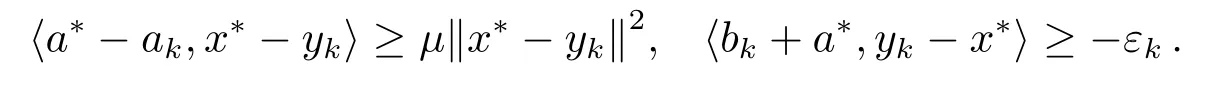
命题3.3令点列{xk}, {yk} 和{wk}由算法1 生成, 令且定义sk为

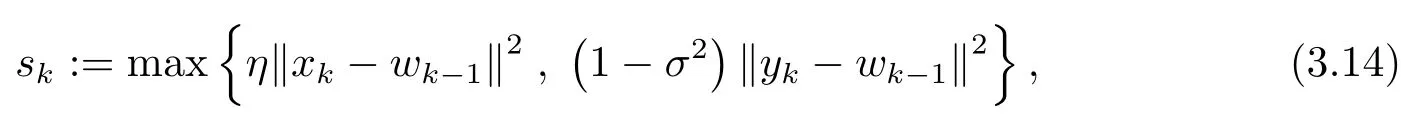
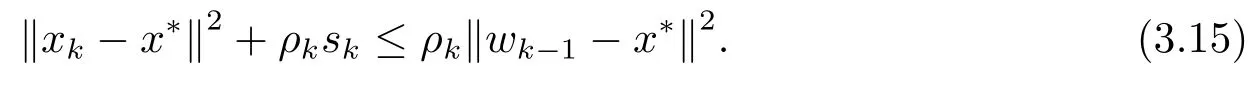
证由(3.4) 式及ρk的定义可知xk=ρk(wk−1−λkvk)+(1 −ρk)yk, 故

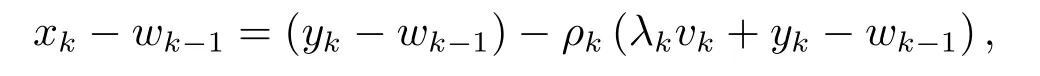
从而由三角不等式可知

由(3.3) 式可知

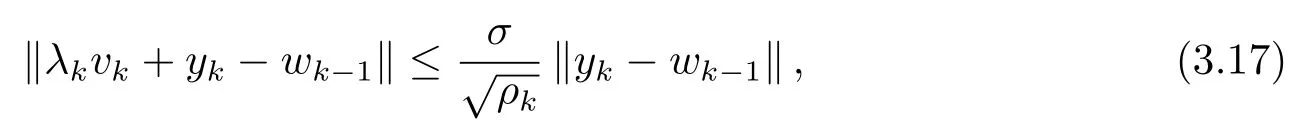
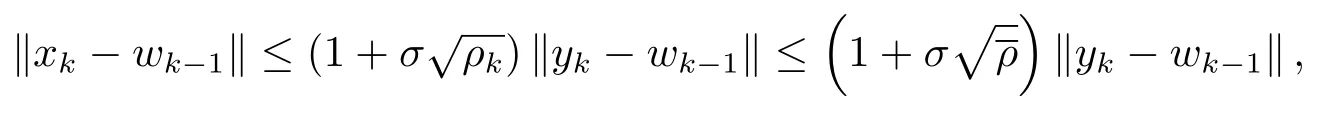
从而

并由(3.7) 和(3.14) 式可得到(3.15) 式.

命题3.4令点列{xk}, {yk}, {wk} 由算法1 生成,sk由(3.15) 式所定义, 并且令

证将x=x∗代入(3.6) 式并由(3.18) 式可得

并由(3.15) 式可知

注意到, 0<ρk≤1, 有ϕk−ϕk−1≤ϕk−ρkϕk−1, 故(3.19) 式成立.

引理3.5[4]令点列使得其中如(3.15) 式所定义, 且满足(3.19) 式.则∀k≥1, 有

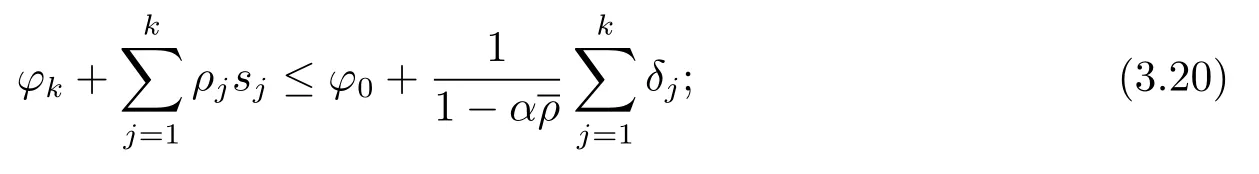
命题3.6令点列{xk},{λk}和{αk}由算法1 产生,如果对于任意的满足下面的条件

则有下面的结论成立

(i) 点列{xk−wk−1}, {yk−wk−1}, {xk−yk}, {vk} 和{εk} 强收敛到零;

(ii) 点列{xk}, {wk−1} 和{yk} 弱收敛到单调包含问题(3.1) 的解.

证由于则并由命题3.4 和引理3.5 可知∀x∗∈存在, 故点列{xk} 有界, 而且由(3.2), (3.3) 和(3.14) 式可知

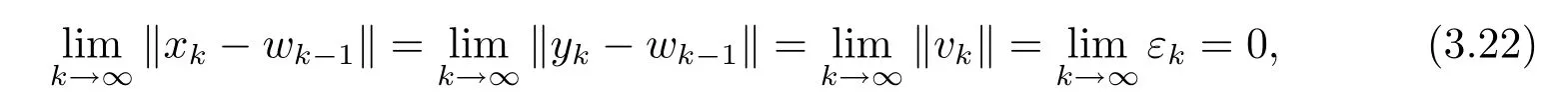
即点列{xk−wk−1}, {yk−wk−1}, {vk} 和{εk} 强收敛到零, 从而{xk−yk} 也强收敛到零.

令x∞∈X 是点列{xk} 的弱聚点, 并令子列使得又由(3.2) 和(3.22)式可得

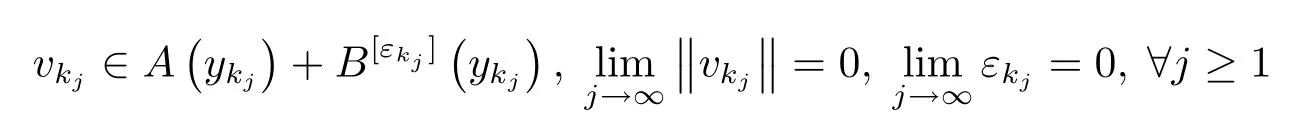
故由命题2.1(v) 可知,x∞∈(A+B)−1(0), 故根据定理2.2 可知点列{xk} 弱收敛到单调包含问题(3.5) 的解.由于{xk−wk−1} 和{xk−yk} 强收敛到零, 因此{wk−1} 和{yk} 也弱收敛到单调包含问题(3.1) 的解.

注3.2由于惯性邻近点算法是算法1 的特殊情况, 因此命题3.6 是文献[4]中定理2.1的推广.

命题3.7令点列{xk}, {yk}, {wk} 由算法1 生成, 令且

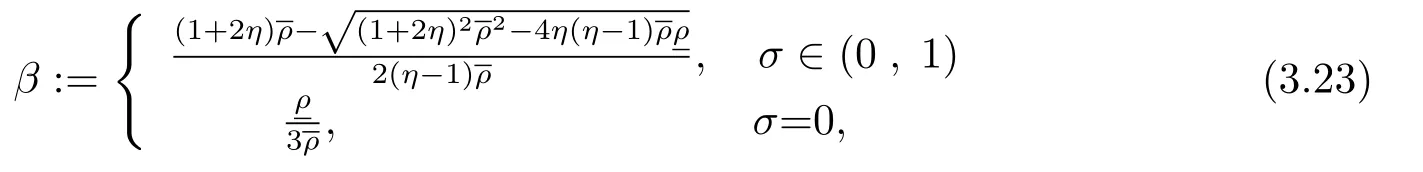
则有q(α)>0, 且∀x∗∈(A+B)−1(0), 有

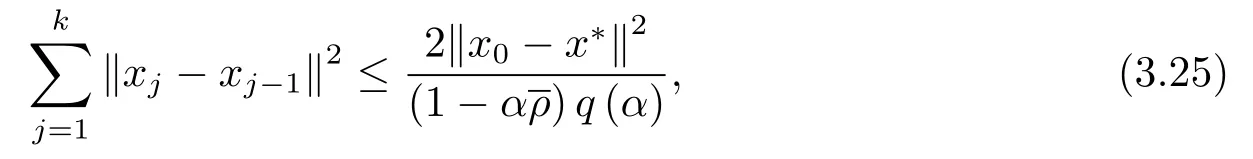
因此点列{xk} 弱收敛到单调包含问题(3.1) 的解.

证由(3.2) 式可知xk−wk−1=(xk−xk−1)−αk−1(xk−1−xk−2), 故

并联立(3.19) 式可得

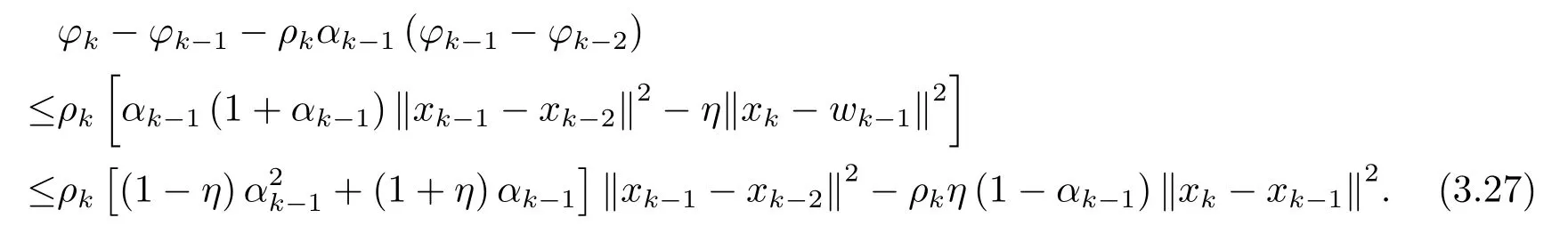
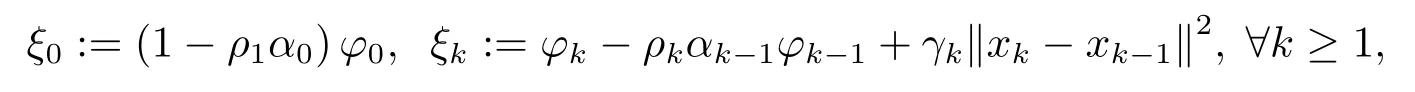
又由于{ρk} 和{αk} 是单增非负数列, 且因此

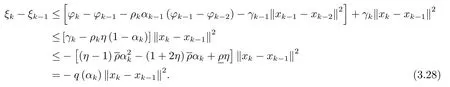
当η∈(0,1) 时, 即σ∈(0,1), 令解得

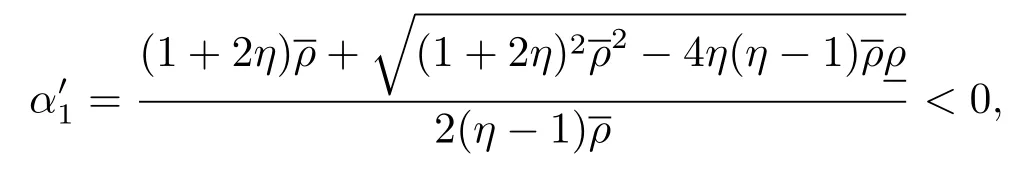
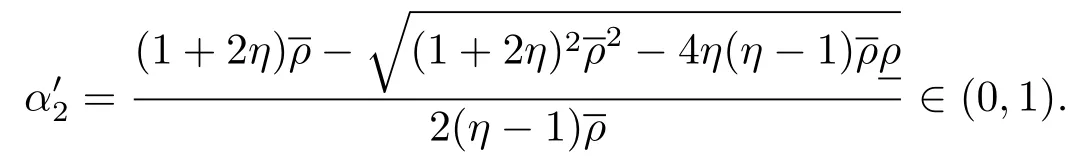
另一方面, 当η=1 时, 即解得

在上述两种情况下, 当αk≤αk+1≤α<β时都有q(αk)≥q(α) >q(β)=0, 从而由(3.28) 式可知

由ξk的定义可得从而由(3.29) 式有

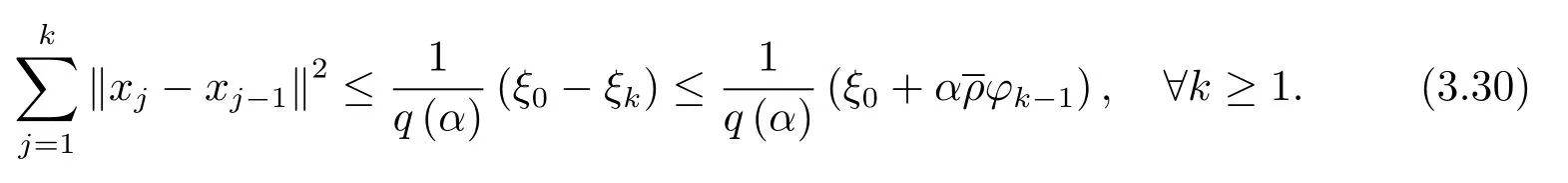
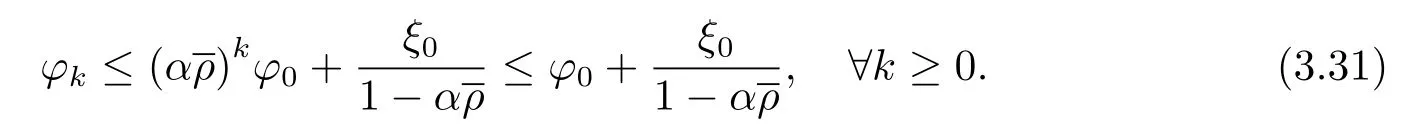
联立(3.30) 和(3.31) 式可得(3.25) 式.

又由于αk∈[0,1), 从而由(3.25) 式可知(3.21) 式成立, 由命题3.6 可知点列{xk} 弱收敛到单调包含问题(3.1) 的解.

注3.3(i) 当σ=0 时, 算法1 退化为惯性邻近点算法, 条件(3.23) 式退化为进一步, 当µ=0 时, 有则条件(3.23) 式退化为因此命题3.7 对文献[4]中的命题2.1 作了推广.

(ii) 如果σ=1, 则对于任意的∈[0,1), 二次函数并不能满足算法收敛的条件, 从而说明了容差参数σ的最大取值范围为[0,1).

推论3.8令点列{xk}, {yk}, {wk} 由算法1 生成.令如(3.23) 式所定义如(3.24) 式所定义, 且x∗∈(A+B)−1(0), 假设αk≤αk+1≤α<β.则∀k≥1, 有

证由(3.20) 和(3.25) 式可得

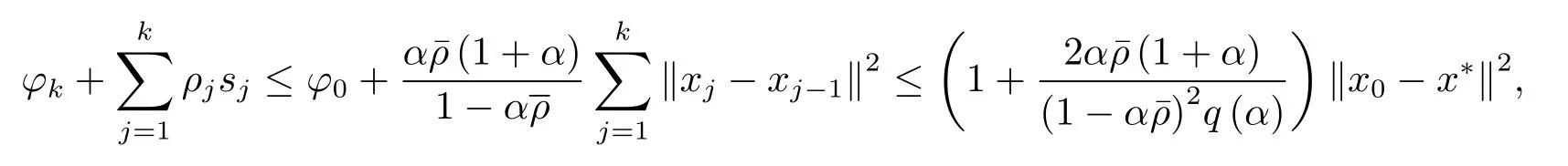
从而由sk的定义可知, (3.32) 式成立.

由柯西不等式及(3.3) 式可知

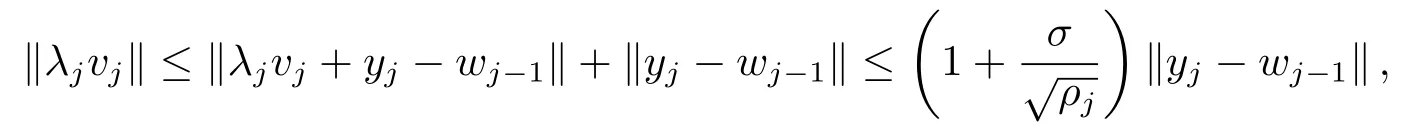
由(3.32) 式可知(3.33) 式成立.

接下来, 本文给出算法1 的非渐近性全局收敛率.

定理3.9令点列{xk}, {yk}, {wk} 由算法1 生成, 令如(3.23)式所定义如(3.24)式所定义假设αk≤αk+1≤α<β.则∀k≥1, 存在i∈{1,...,k} 使得vi∈A(yi)+B[εi](yi), 而且

证令x∗∈(A+B)−1(0)使得由(3.32) 和(3.33) 式可知, 对∀k≥1存在i∈{1,...,k} 使得

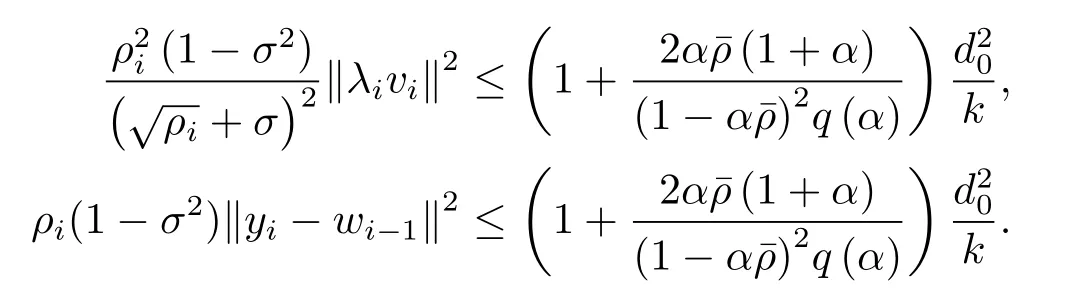
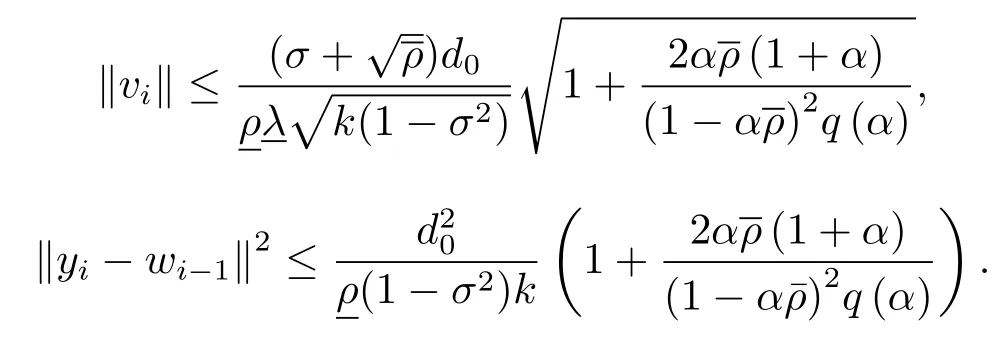
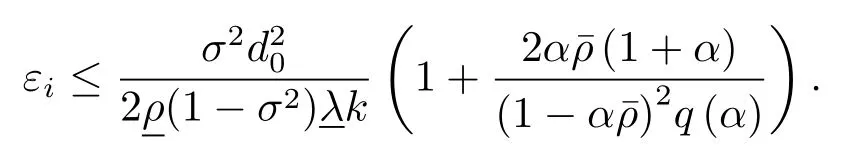
注3.4定理3.9 说明了算法1 的全局逐点收敛率为

4 求解单调包含问题的惯性Tseng’s 向前向后算法

在这部分, 本文考虑单调包含问题

其中F:X →X 是(单值) 强单调和L-Lipschitc 连续算子, 即存在µ≥0 和L>0 使得

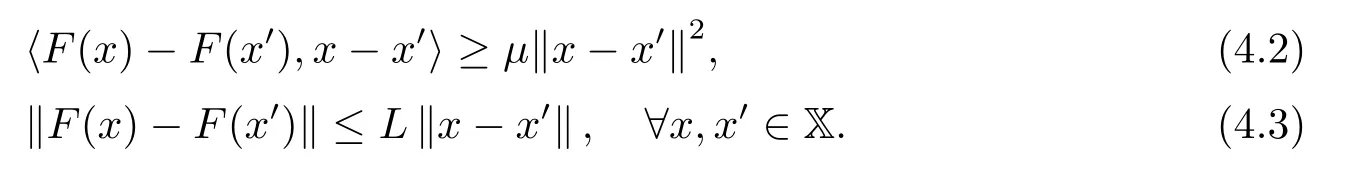
T:X ⇒X 是极大单调算子.假设问题有解, 即(F+T)−1(0) 非空.

下面本文给出求解问题(4.1) 的惯性Tseng’s 向前向后算法.

算法2

步骤0任取初始点x0=x−1∈X, 任意给定α∈[0,1),α0∈[0,α],σ< 1,k=1, 令任意给定λ0∈[0,];

步骤1选定αk∈[αk−1,α], 定义

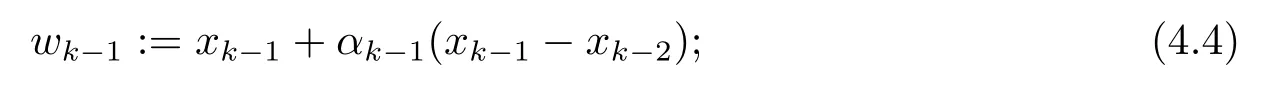
步骤2选定0<λk≤λk−1, 计算yk

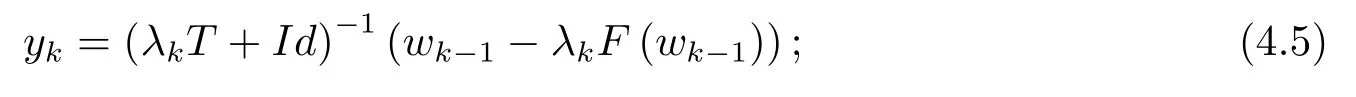
步骤3计算xk

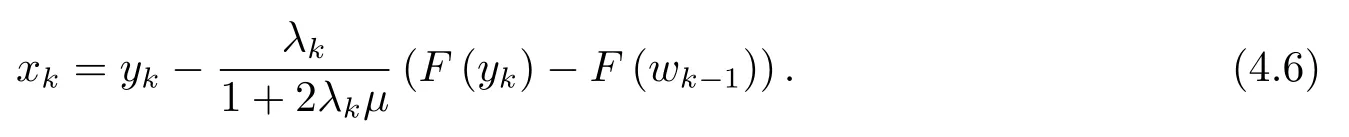
令k:=k+1, 返回步骤1.

注4.1(i) 当αk≡0,时, 算法2 退化为文献[12]中的算法2.

(ii) 算法2 是算法1 在选定εk≡0 时的特殊情况.事实上, 在算法2 中定义:A:=F,B:=T, 且

从而可知

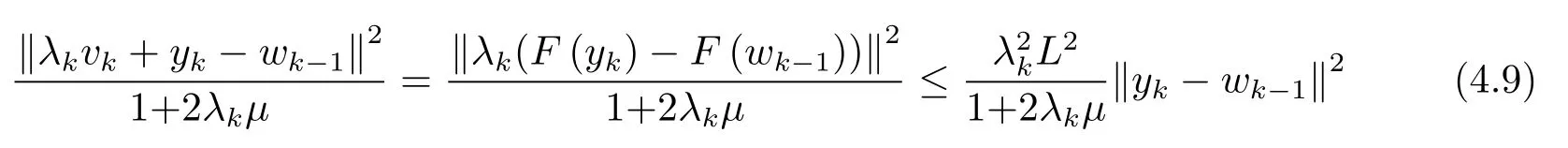
将(4.8) 式代入(4.6) 式可得

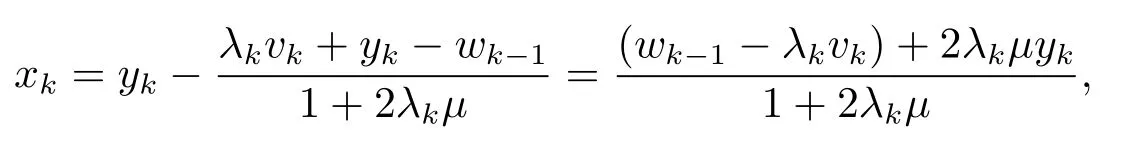
即算法1 的步骤3 满足.综上可知, 算法2 是算法1 的特殊情形.

由于算法2 是算法1 的特殊情况, 因此由命题3.6, 3.7 和定理3.9 可得到下面的结论.

命题4.1令点列{xk} 由算法2 产生, 令和{vk}如(4.7)式所定义,其中x∗∈(F+T)−1(0),β如(3.23)式所定义如(3.24) 式所定义, 假设αk≤αk+1≤α<β.则有下面的结论成立

(i) 点列{xk} 弱收敛到单调包含问题(4.1) 的解.

(ii) 对任意的k≥1 存在i∈{1,...,k} 使得vi∈F(yi)+B[εi](yi), 而且

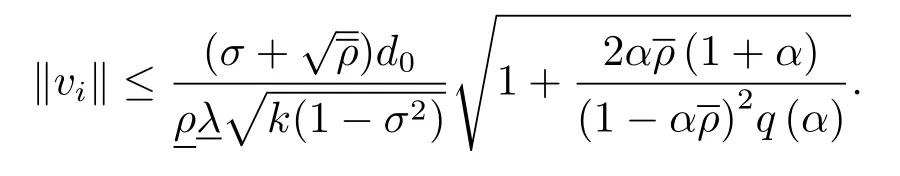
注4.2(i) 命题4.1 说明了算法2 的全局逐点收敛率为

5 求解原始―对偶问题的惯性非精确Spingarn’s 部分逆算法

接下来, 本文考虑原始―对偶问题[17].找到x,u∈X 使得

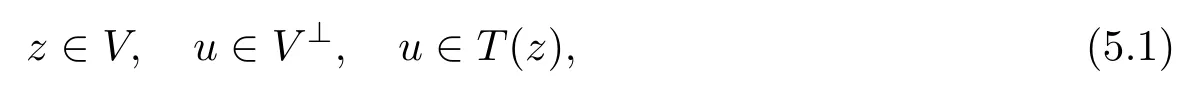
其中T:X ⇒X 是实Hilbert 空间X 中的极大单调算子,V是闭子空间,V⊥是V的正交补空间.特别的, 当V=X 时, 问题(5.1) 退化为单调包含问题(1.1).假设T是κ-强单调和L-Lipschitc 连续算子.

定义5.1[18]称TV: X ⇒X 是极大单调算子T: X ⇒X 关于X 中的闭子空间V的Spingarn’s 部分逆算子, 如果TV满足

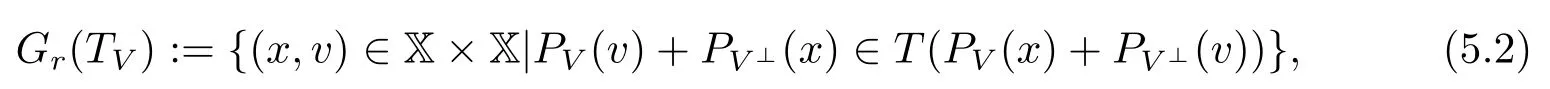
其中PV和PV⊥分别是V和V⊥上的正交投影.

由定义可知, 原始―对偶问题(5.1) 等价于单调包含问题0 ∈TV(x), 而且若x∗是单调包含问题0 ∈TV(x∗) 的解, 则z∗=PV(x∗),u∗=PV⊥(x∗) 是原始―对偶问题(5.1) 的解.

引理5.2[19]令T:X ⇒X 是X 中的极大单调算子,V是X 中的闭子空间, 且ε>0, 则(TV)[ε]=(T[ε])V.

引理5.3[20]如果极大单调算子T是κ-强单调和L-Lipschitc 连续算子, 则它的关于V的部分逆TV是µ-强单调的, 其中

下面给出求解原始―对偶问题(5.1) 的惯性非精确Spingarn’s 部分逆算法如下

算法3

步骤0任取初始点x0=x−1∈X, 给定α∈[0,1),α0∈[0,α],σ∈[0,1),k=1;

步骤1选定αk∈[αk−1,α], 计算

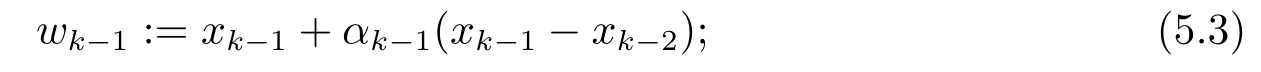
步骤2找到zk,uk∈X,εk≥0, 使得

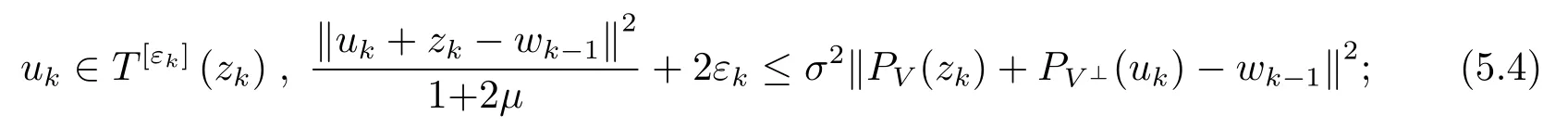
步骤3计算xk

令k:=k+1, 返回步骤1.

注5.1(i) 当αk≡0 且µ=0 时, 算法3 退化为文献[21]中的算法2.

(ii) 算法3 是算法1 在选定λk≡1 时的特殊情况.事实上, 在算法3 中定义A:=TV,B:=0, 且

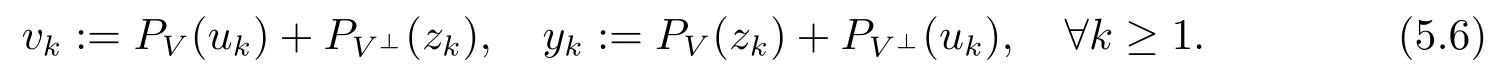
由引理5.2, (5.2) 及(5.4) 式可知

从而由(5.6) 式可知vk∈(TV)[εk](yk)=A[εk](yk)+B(yk), 且

由λk≡1, (5.6), (5.7) 及(5.4) 式可知

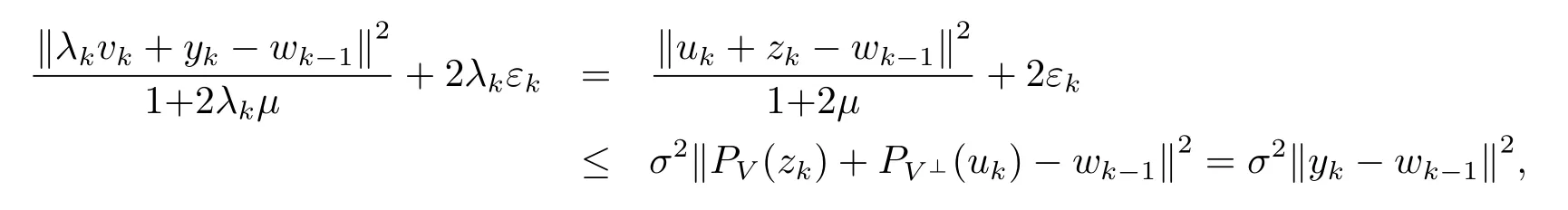
即算法1 的步骤2 满足.由λk≡1, (5.6), (5.7) 及(5.5) 式可知

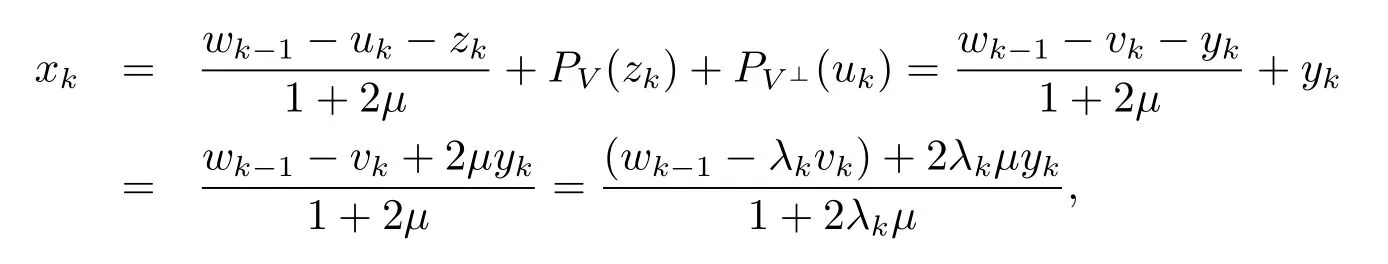
即算法1 的步骤3 满足.故算法3 是算法1 的特殊情形.

由于算法3 是算法1 的特殊情况, 因此由命题3.6, 3.7 和定理3.9 可得到下面的结论.

命题5.1令点列{xk} 由算法3 产生, 且{λk}, {vk} 和{yk} 如(5.6) 式所定义, 令其中x∗是单调包含问题0 ∈TV(x∗)的解.令

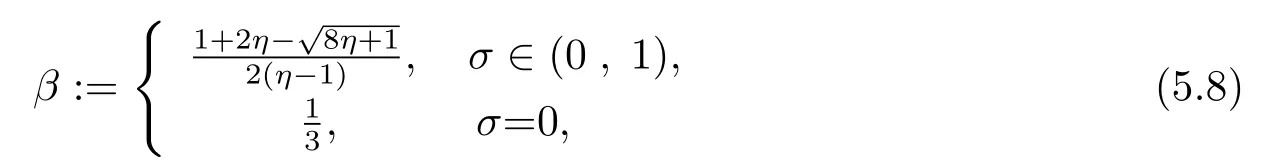
定义实函数q() 为

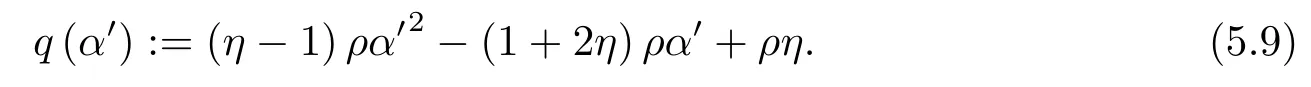
假设αk≤αk+1≤α<β, 则有下面的结论成立

(i) 点列{xk} 弱收敛到单调包含问题0 ∈TV(x) 的解.

(ii) 对任意的k≥1 存在i∈{1,...,k} 使得vi∈(TV)[εi](yi), 而且

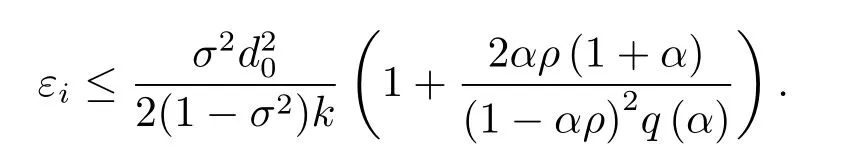
注5.2有序对(PV(xk),PV⊥(xk)) 弱收敛到原始―对偶问题(5.1) 的解.

6 总结

本文提出了一种新的求解单调包含问题的惯性混合邻近外梯度算法, 并得到了该算法在实希尔伯特空间中的弱收敛性和非渐近全局收敛率.惯性混合邻近外梯度算法包含一些现有的算法, 例如Tseng’s 向前向后算法和Spingarn’s 部分逆算法等.利用该算法的框架可以设计求解优化问题与变分不等式问题的新的算法.