广义(2+1) 维浅水波类方程的有理解
杜亚红, 银山
(内蒙古工业大学理学院,内蒙古呼和浩特010051)
1 引言
近年来, 数学、物理等各个领域都在研究孤子, 其中求解孤子方程的精确解是应用数学领域中的热门话题之一.目前已有了多种求解孤子方程精确解的方法, 如: 双线性导数法[1]、反散射方法[2,3]、Darboux 变换[4,5]、tanh 方法[6,7]等.
这些方法中, 双线性导数法是由著名的日本数学、物理学家Ryogo Hirota 提出, 他是在研究非线性偏微分方程的解的过程中, 利用摄动法得到一种双线性方程, 并定义出一种新的微分算子――Hirota 双线性算子
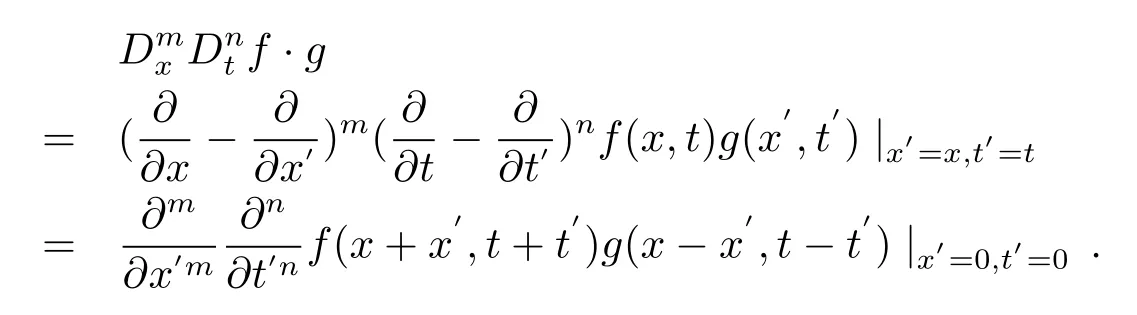
如果某一方程具有双线性形式, 那么该方程就能具备可积性.在Hirota 双线性算子基础上,马文秀[8−11]教授提出了一般的双线性微分算子
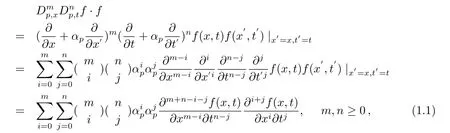
其中p是素数且p≥2, 并且(1.1) 式中的满足
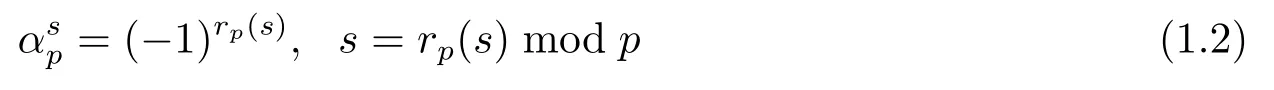
本文中, 借助这个一般双线性算子(1.1), 从(2+1) 维浅水波方程[12,13]

的双线性形式, 构造出p=3 对应的一个广义浅水波类方程.再通过求解该方程的一般双线性方程的多项式解, 构造了该广义浅水波类方程的有理解.
2 广义(2+1) 维浅水波类方程
(2+1) 维浅水波方程(1.3) 通过变换u=2(lnf)x得到其双线性形式
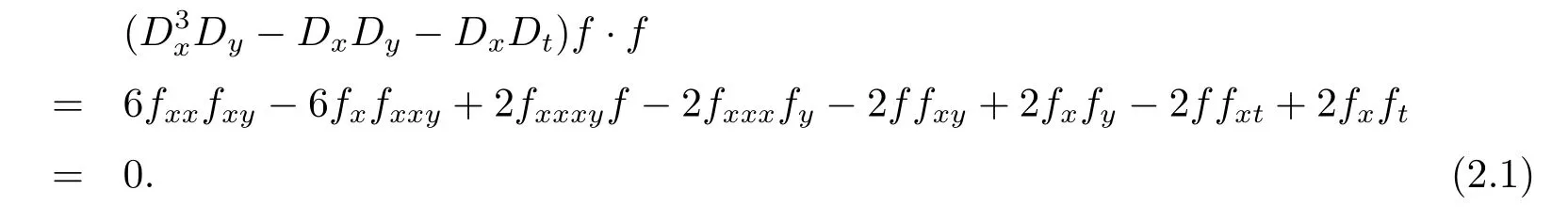
通过计算可以证明, (2.1) 即为p=2 时(D32,xD2,y−D2,xD2,y−D2,xD2,t)f·f的形式.
根据一般的双线性算子(1.1), 求得
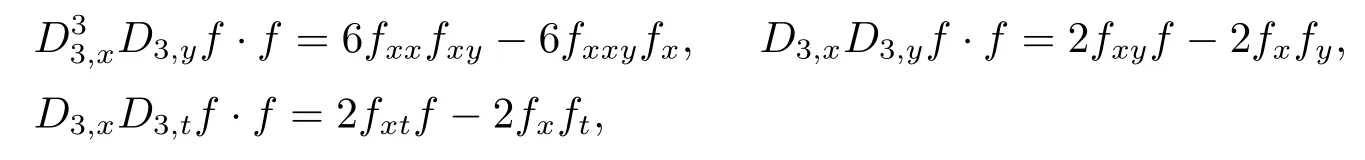
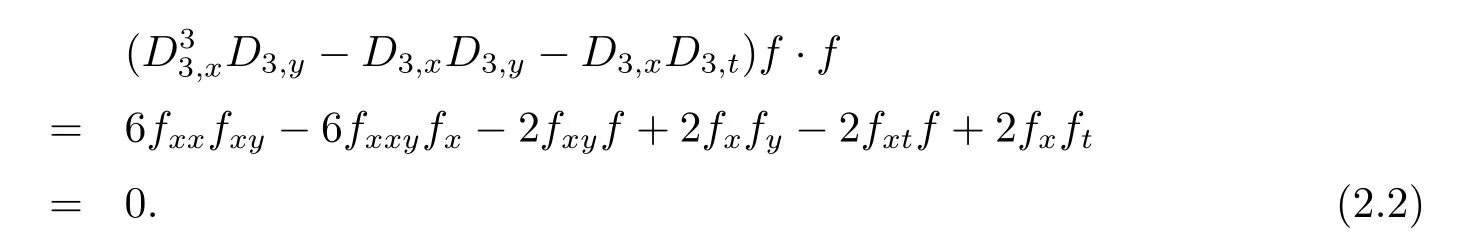
利用贝尔多项式理论[14−16], 选取变换

可得
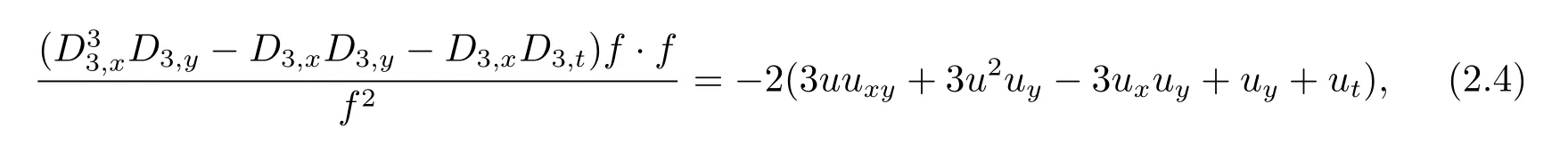
则有广义(2+1) 维浅水波类方程
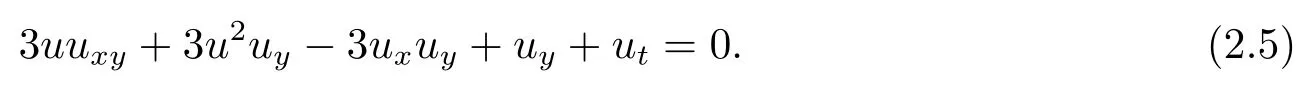
比较浅水波方程(1.3) 和广义浅水波类方程(2.5), 可以发现(2.5) 的双线性形式(2.2) 比(1.3)的双线性形式(2.1) 更简单一些, 但(2.5) 比(1.3) 更具有非线性.
根据变换(2.3), 若f是方程(2.2) 的解, 则有u为方程(2.5) 的解.
3 广义(2+1) 维浅水波类方程的有理解
借助数学软件Mathematica, 令
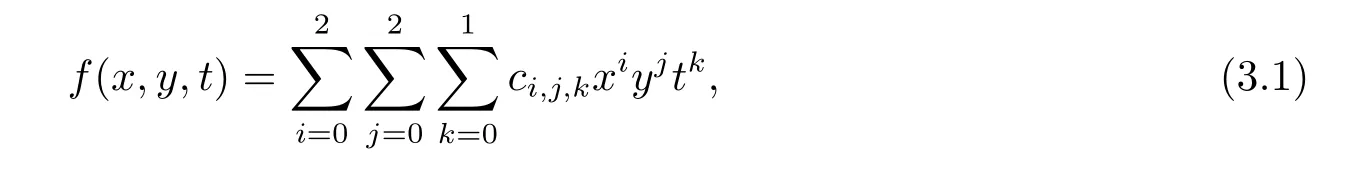
代入(2.2) 式, 可以得到它的一系列的多项式解

对应地, 根据变换u=(lnf)x, 可以求得广义(2+1) 维浅水波类方程(2.5) 的4 类有理解.
第一类有理解

其中
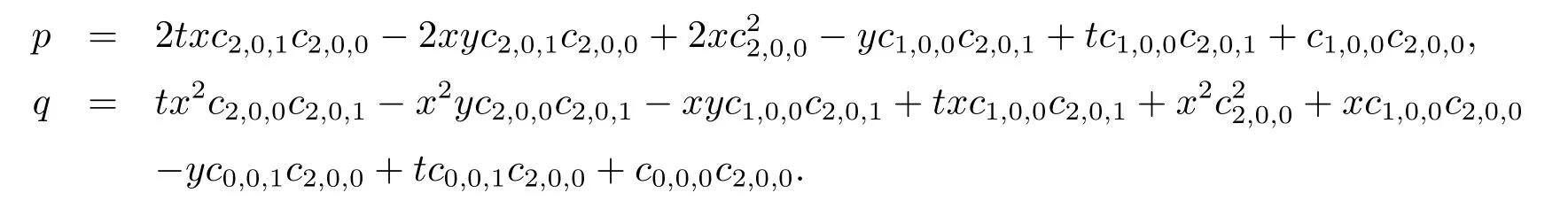
第二类有理解
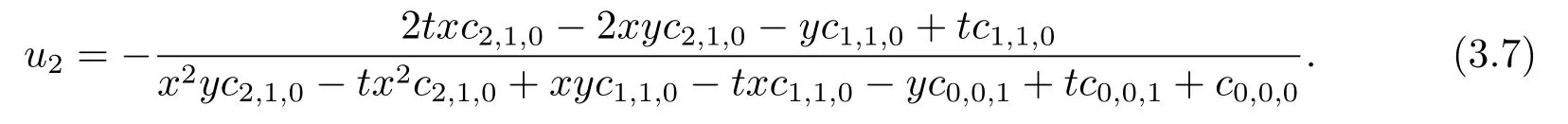
第三类有理解
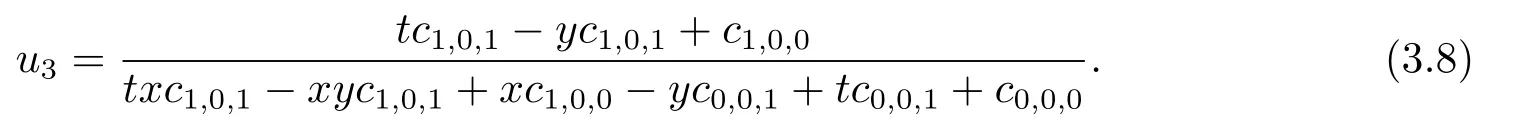
第四类有理解
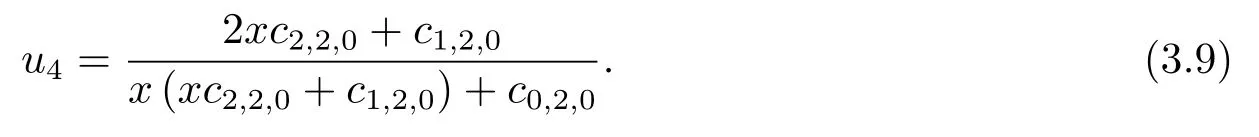
4 结论分析
本文中, 在(2+1) 维浅水波方程(1.3) 的基础上, 利用一般的双线性微分算子(1.1), 当素数p=3 时, 得到了具有一般双线性形式的微分方程――广义(2+1) 维浅水波类方程(2.5).借助广义(2+1) 维浅水波类方程(2.5) 的一般双线性形式, 利用数学软件Mathematica, 得到了方程(2.5) 的4 类有理解.

图1:解(4.2) 在t=1 时的三维图(左), 密度图(中) 和等高线图(右)
当参数被选取为
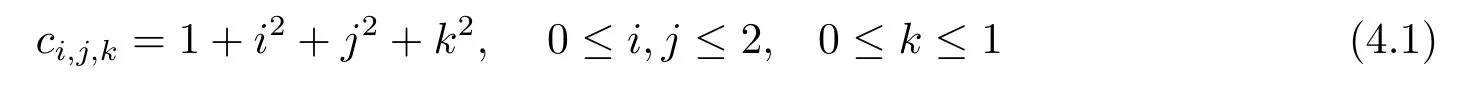
时, 解(3.6) – (3.8) 分别为
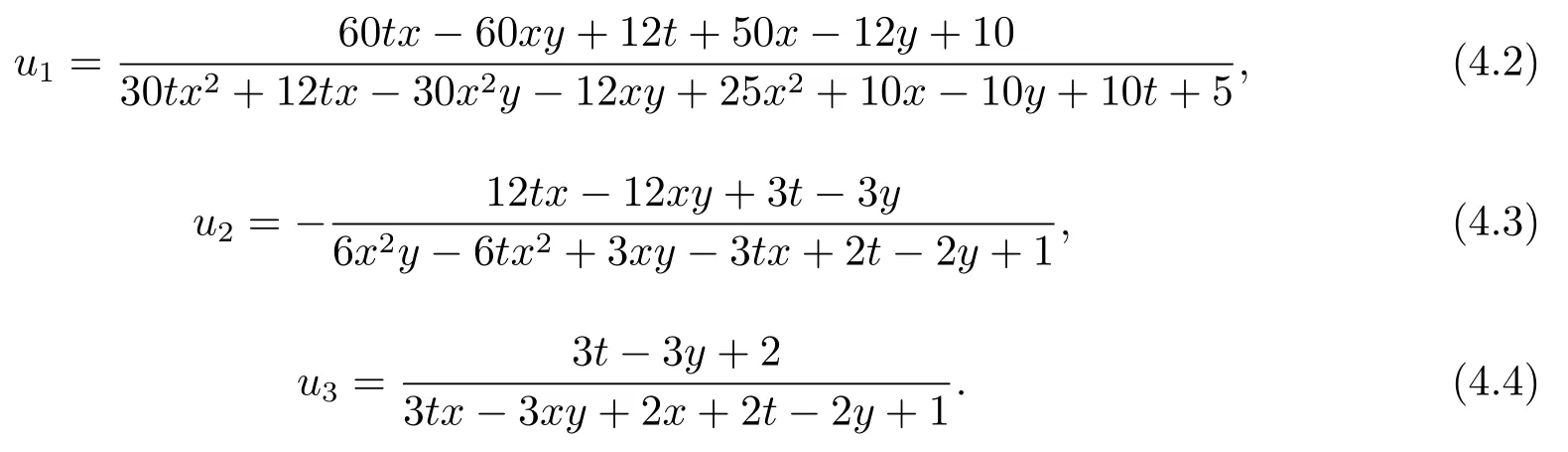
即得到广义(2+1) 维浅水波类方程(2.5) 的3 类特殊有理解.解(4.2), (4.3) 和(4.4) 在t=1时刻的三维图、密度图和等高线图如图1–3 所示.从这些图能看出,y=0 直线附近解曲面变化很大, 且当x趋于无穷大时这些解都趋向于0, 即解曲面趋向水平面.

图2:解(4.3) 在t=1 时的三维图(左), 密度图(中) 和等高线图(右)
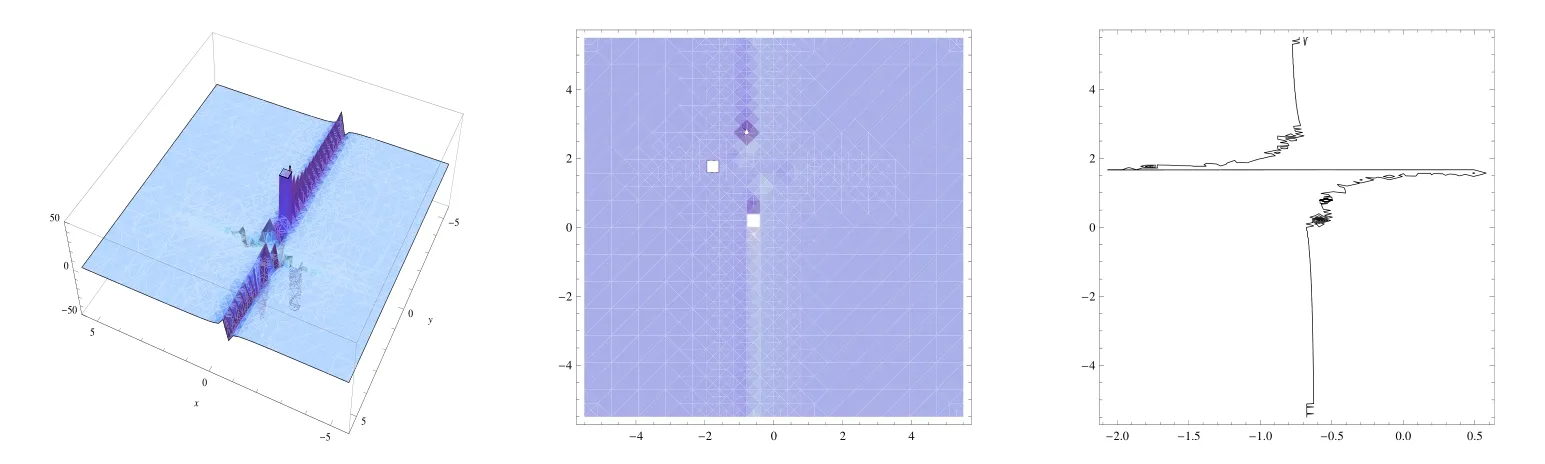
图3:解(4.4) 在t=1 时的三维图(左), 密度图(中) 和等高线图(右)

