基于制动距离的载货汽车制动安全状态辨识方法研究

张景海，张萌，柴萌，李世武，戚培心

（1.吉林大学 交通学院，长春 130022；2.长春工程学院，长春 130000）

公路运输中载货汽车的安全问题一直是当前社会关注的重点，国内外许多学者对此进行了深入研究。如Tonchev A［1］应用仿真分析软件对车辆的制动性能开展了研究；Om Prakash Singh等人［2］进行了车辆制动相关试验，研究了制动鼓的受热变化规律；烟台大学袁春静等人［3］利用ANSYS软件对制动鼓进行了有限元建模分析；长安大学余强基于WEBB C R［4］和 GREIG J C［5］等人的研究成果对重型商用汽车制动失效特性进行了研究。但现有研究领域大多偏重于制动器的设计和改进，或者对制动器某一性能进行仿真分析，很少涉及从制动距离的角度对载货汽车的制动安全状态进行辨识。同时现有的制动距离模型存在相关参数过多、模型过于复杂、计算工作量大等问题，在实际应用过程中存在诸多不便。

本文首先提出了制动距离理论模型，并以解放赛龙CA1169PK2L2EA80载货汽车为例，通过试验标定，进一步简化完善了该模型。随后进行模型的实车应用研究，找到判断载货汽车危险状态的量化指标，确定危险阈值范围，最终提出了一种新的基于制动距离的载货汽车制动安全状态的辨识方法。此方法具有模型简易、参数易于量化、方便测量等特点，为开发载货汽车制动安全状态检测及预警系统奠定了理论基础。

1 制动距离理论模型建立

制动距离s包括制动器起作用和持续制动两个阶段的距离，分别用s1和s2表示，则：

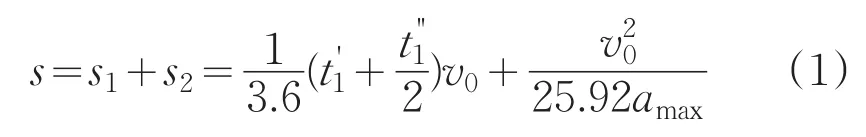
式中，a为制动减速度；制动起始车速为v0；制动器间隙传递延迟时间为；制动力增长时间为；Fμ为制动器制动力；Fφ为附着力。

由式（1）可知，制动器起作用时间、制动减速度以及制动起始车速是影响制动距离的主要因素。

正常行驶的汽车，其行驶方程式为：

式中，Ft为驱动力；Fw为空气阻力；Fi为坡道阻力；Fj为加速阻力；Ff为滚动阻力。

紧急制动条件下，车辆传动系统与发动机分离，驱动力Ft下降为零，车轮与传动系统转速降低。在此条件下，转动惯量消耗能量较小，可忽略传动系统的内部阻力，制动减速度公式如下：

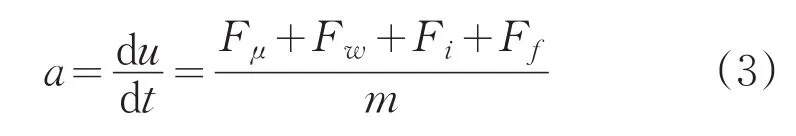
在整个制动过程中，平均滚动阻力为：

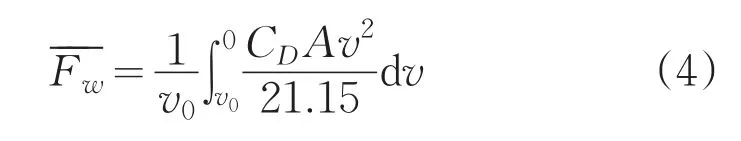
平均空气阻力为：

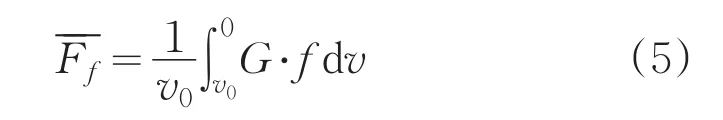
将公式（4）和公式（5）带入公式（1）中得到制动距离公式（6）：

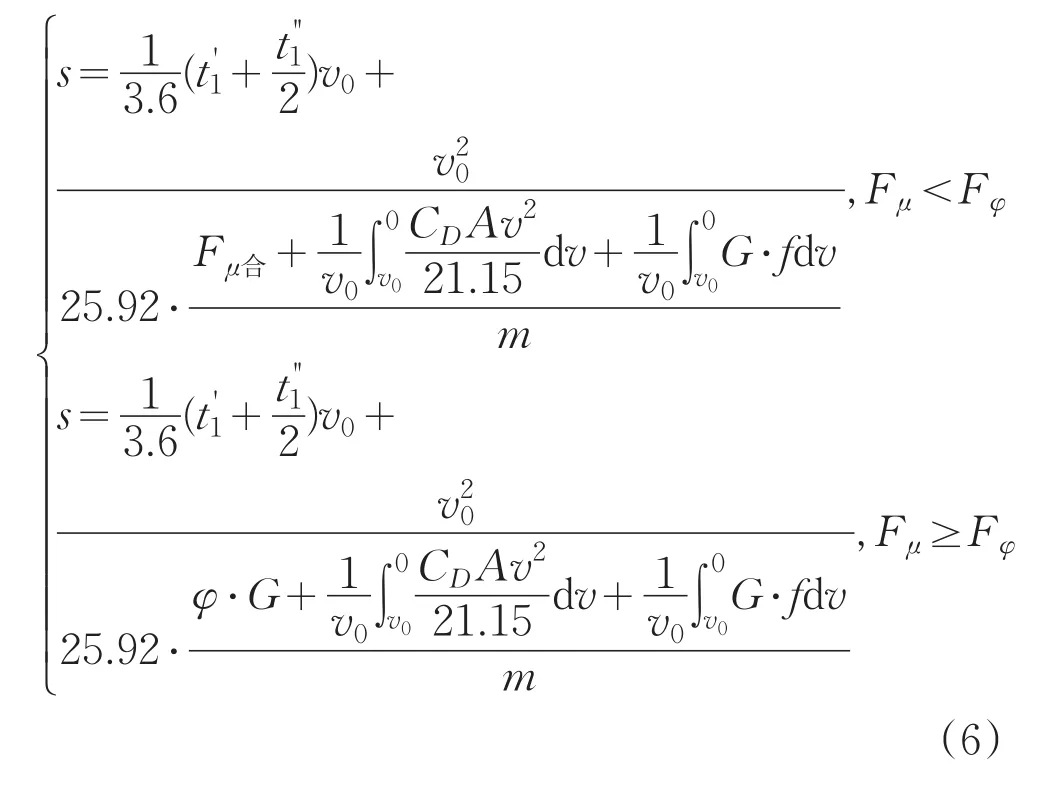
式中，G为车辆总重力；m为整车质量；CD为空气阻力系数；f为滚阻系数。

2 实车应用中模型参数的试验标定

对理论模型进行实车应用时，可由已知试验车辆的整车参数得到其迎风面积、整车质量以及制动器制动力等数值。由于不能直接得到车辆行驶过程中空气阻力系数以及滚阻系数，因此需要通过试验手段近似测出试验车辆的空气阻力系数值和滚阻系数值。

滑行中的汽车上主要阻力有空气阻力、坡道阻力以及滚动阻力（传动系阻力影响较小，可忽略不计）。试验路面平坦，坡度角可近似为零，此时坡道阻力的影响可忽略不计。为获得较高的计量精度，本文采用车辆滑行试验的方法（GB/T12536—90）进行制动距离理论模型的参数标定。

2.1 试验目的

根据前文所述，利用试验车辆的制动器结构参数可间接得到制动器制动力等数值，但不同的试验车辆具有不同的空气阻力系数和滚动阻力系数，因此需要对其进行试验标定。本次标定根据国标《GB/T12536—90汽车滑行试验方法》的相关规定进行滑行试验设计，进而得到车辆制动减速度受空气阻力和滚动阻力的影响情况。

2.2 试验条件

试验车型为解放赛龙CA1169PK2L2EA80；试验道路标定10 km沥青混凝土道路，且路面干燥平坦，道路车辆较少，基本无干扰。

2.3 试验方法

开始试验时，车辆空载加速至60 km/h。当车辆到达标记起始点时，将加速踏板松开，车辆档位变为空挡，使之开始滑行，一直到其完全停止。车辆滑行时，由车外试验人员及车内人员分别记录车辆到达指定标杆处的时间及车速。反向进行滑行试验，起始点设置为靠近上次试验停车点的标杆。前后试验尽量保证滑行路段重合，并在整个过程中重复操作。将车辆调整为满载和半载并重复试验。

2.4 数据整理

记录实验过程中相应标杆处的车速、所需时间及最终滑行距离，并整理各载荷状态下车辆的数据。其中空载试验的一组数据如表1所示。

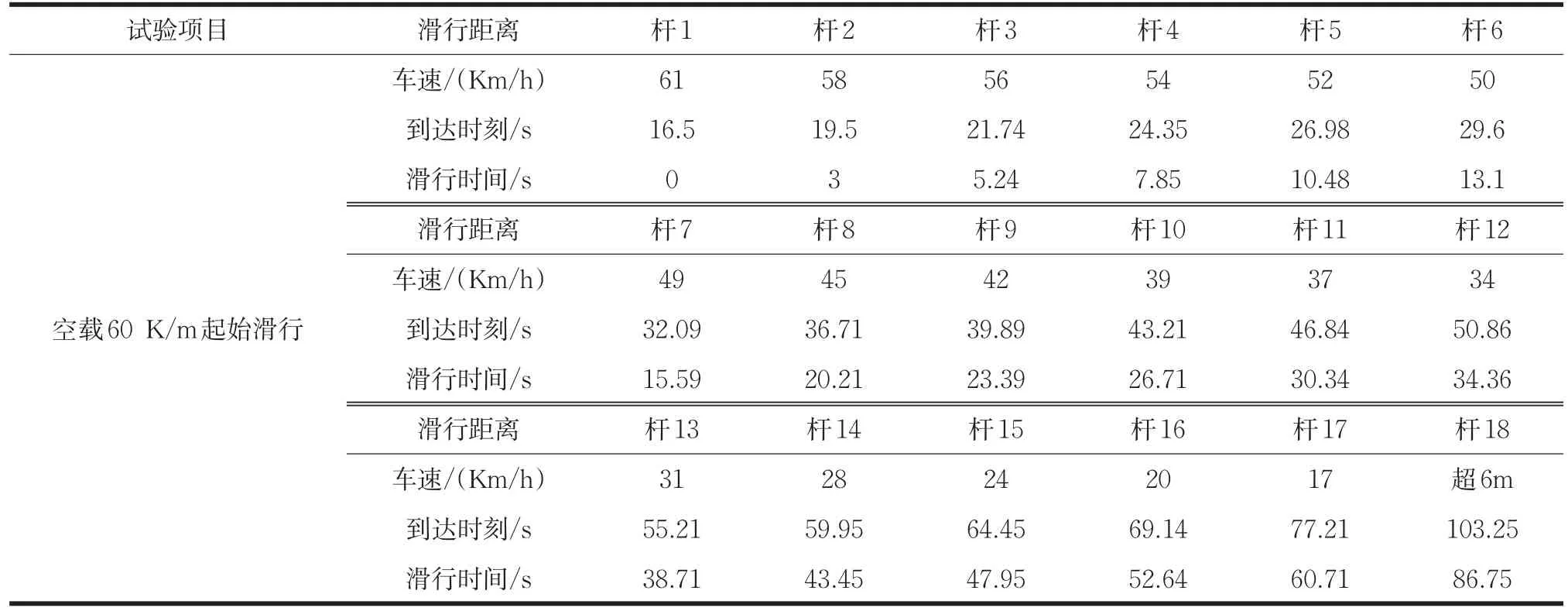
表1 空载60 Km/h滑行试验数据

2.5 数据处理

查阅相关研究结果可以得到，通常使用速度的二次多项式表示滚阻系数。但由于载货汽车的胎压较高，其滚阻系数经验公式与车速近似呈线性关系，在此种情况下滚阻系数计算模型使用公式（7）：

式中，v表示车辆行驶速度；a、b为待定系数。

研究空气阻力系数时，相关文献［6-7］及试验结果［8-9］均表明“空气阻力值与车辆速度的平方近似呈正比关系”，于是将空气阻力计算模型表示为：

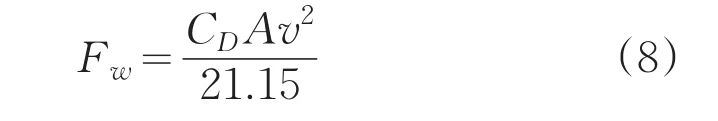
式中，v表示汽车行驶速度；CD表示空气阻力系数；A表示汽车迎风面积。

滑行中的汽车由于滚动阻力和空气阻力的共同作用而减速，其行驶方程式可表示为：

整合以上公式得：

式中，δ表示旋转质量转换系数，取决于车辆的质量，可根据汽车理论推荐值得到：

使用数学方法对公式（10）进行处理，公式左右两端同时乘以滑行距离s的微分ds，并带入v=ds/dt，同时进行积分变换，可以得到：

由以上公式可以得到，滑行初速度v0，滑行距离S和滑行时间T是以a，b，c为系数的特定系数方程，故得到方程组：

选择试验数据中的三个初速度对应的滑行距离和滑行时间，求解上述方程组，即可求得相对应的一组未知数a、b和c。

整理试验数据，对相同载荷条件下多次试验数据进行求和去均值，并利用上述方法处理整合后的数据，进而求得各种载荷条件下a、b、c的值。之后再对不同载荷条件下数据取均值，其最终处理结果归纳如表2所示。

根据上表可得到最终处理结果a=0.012 5，b=0.000 42，c=0.000 016 5。导入试验车型参数，进而得到该试验车型的滚阻系数和空阻系数：

由试验车型的整车和制动系统参数，可以得到前后制动器的制动力Fμ前=0.064⋅pμ，Fμ后=0.095⋅pμ，p为制动管路压力，则车辆四个制动器总制动力为Fμ合=0.318⋅pμ。各种摩擦材料摩擦系数的稳定值约为0.3～0.5，少数材料可达到0.7，在制动器相关计算中一般取0.3～0.35［10］。本文取试验车型的制动器摩擦系数μ=0.35，得车辆制动器制动力：Fμ合=0.318⋅pμ=0.112p。

带入标定试验确定的滚阻系数和空阻系数，得到平均风阻表达式：

平均滚阻表达式：

表2 滑行试验数据处理表格

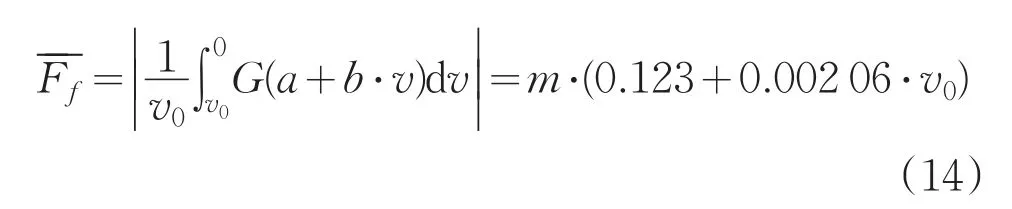
将以上内容整理并带入制动距离理论模型，得到简化后的理论模型公式（15）。

3 基于制动距离模型的制动安全状态辨识方法

车辆行驶环境通常分为两种：第一种环境为道路条件良好，视野开阔，车流顺畅；第二种环境为天气及道路条件较差，车流迟缓，视野狭窄。考虑前后两车间安全距离时，在第一种环境条件下，必须以前车紧急制动为前提，后车在随之紧急制动后不撞上前车且停车后与前车保持适当的安全间距。在第二种环境条件下，前车在运行中可能重物脱落或者突然原地停驶，此时应满足跟随车辆驾驶员从发现前车停驶后实施紧急制动到制动完成后仍能保持与障碍物的安全间距。按此原则确定的距离即为该种状况下车辆行驶的最小安全距离。

图1 考虑前车制动的安全距离

图2 极限情况下的安全距离

由图1和图2可知，最小安全距离与制动非安全距离相关，两者相差一个安全间距（一般取5 m）。本文中应用到的最小安全距离以第二种环境为参考，即极端制动条件下，车辆在行驶过程中与前车应保持的安全距离，用公式（16）表达为：

t表示驾驶员反应时间与制动响应时间的总和，一般取0.5～1.8 s，在本文中取1.8 s。研究试验车型相关实验数据后发现，紧急制动管路压力在正常状态下P=0.56 MPa，制动器提供的总制动力为Fμ=6.27×104。在车辆空载条件下地面附着力为Fφ=φ⋅G=0.8×4 780×9.8=3.75×104，制动器制动力Fμ大于地面附着力Fφ，则应用Fμ≥Fφ时的制动距离模型求解制动距离；当装载后整车质量达到8t以上时，地面附着力Fφ=φ⋅G≥0.8×8 000×9.8=6.27×104，制动器制动力Fμ小于地面附着力Fφ，则应用Fμ＜Fφ时的制动距离模型求解制动距离。通过计算可得到不同载荷及车速条件下的制动距离阈值Sy，如表3所示。

国标《GB12676-1999汽车制动结构、性能和试验方法》明确说明了对不同车辆制动距离的要求，参考国标，可以利用极限条件确定相关影响因素阈值。如表4所示，各类车辆必须达到表中规定的最低性能要求。本文中选用车型最大总质量为15 000 Kg，符合表中N3类车辆标准。所以本车制动时的制动距离应该小于即：

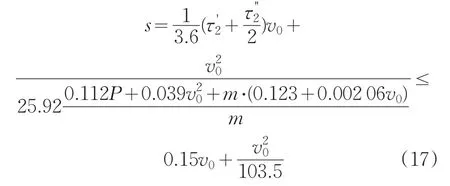
按照国标制动距离的要求，分析后得到不同载荷、不同行驶速度条件下，制动管路压力应满足公式（18）。

表3 不同载荷及车速下的制动距离阈值表

表4 不同类型车辆的制动最低性能要求

由此可通过计算得到制动管路压力阈值Py。

综上得到基于制动距离的载货汽车制动安全状态辨识方法：

（1）在车辆实际行驶过程中，检测车辆与前方障碍物的距离Sj，将其与制动距离阈值Sy进行比较，如果Sj＞Sy，则说明车辆制动安全状态正常。

（2）基于国家标准要求，在紧急制动时，检测制动管路压力Pj，并与阈值公式计算的阈值Py进行比较，若Pj＞Py，则说明车辆制动安全状态正常。

4 结论

（1）从载货汽车制动减速度的影响因素分析入手，建立了载货汽车的制动距离理论模型。

（2）以解放赛龙载货汽车为例进行了模型的实车应用研究。通过滑行试验，对试验车辆的空气阻力和滚动阻力参数进行标定，进一步简化了模型。

(3）提出了一种新的基于制动距离的载货汽车制动安全状态辨识方法，即通过检测车辆与前方障碍物的距离以及制动管路压力可判断车辆的制动安全状态。

本文提出的基于制动距离的载货汽车制动安全状态辨识方法具有模型简易，参数易于量化，方便测量等特点，为后期开发载货汽车制动安全状态检测及预警系统奠定了理论基础。