模袋混凝土复合断面衬砌渠道糙率系数原型观测试验研究
翟东汉,何武全,2,赖红兵,娄宗科,霍轶珍
(1.西北农林科技大学水利与建筑工程学院,陕西 杨凌 712100;2.旱区农业水土工程教育部重点实验室,陕西 杨凌 712100;3.中华人民共和国水利部,北京 100053;4.河套学院,内蒙 巴彦淖尔 015000)
随着水资源的日益紧缺,水资源的优化配置及节水灌溉的实施变得越来越重要,我国作为农业大国,通过进行渠道衬砌防渗的方式来节约水资源是缓解农业用水压力的重要途径之一[1]。渠道衬砌防渗可以有效减少输水过程中的渗漏损失,是目前应用最广泛的节水灌溉工程技术措施之一[2]。然而,冻胀破坏是制约我国北方寒冷地区渠道衬砌防渗工程建设的一个关键因素,为了解决这一问题,近年来北方灌区引进了模袋混凝土渠道衬砌技术。模袋混凝土是由上下两层高质量机织化纤布制成模袋,内充混凝土或砂浆凝结后形成高密度、高强度的固结体,具有施工机械化程度高、施工速度快、适应变形能力强、抗冻胀性能好等优点[3-5]。我国北方寒冷地区已有大量工程成功运用模袋混凝土渠道衬砌技术,如河套灌区的东风一干渠渠道衬砌防渗工程、沈阳市浑浦灌区渠道防渗衬砌工程、引滦输水明渠护坡工程等[6-8]。目前,模袋混凝土衬砌渠道的形式分为全断面衬砌和复合断面衬砌,主要应用于大中型渠道,当地下水位埋深较大、渠道底宽较窄时,通常采用模袋混凝土全断面衬砌形式;当地下水位较高、冻胀破坏严重时,通常采用复合断面(边坡为模袋混凝土,渠底为砂砾石或土基)衬砌形式。国内对复合断面衬砌渠道的糙率系数已经有了一些研究,黄宽渊[9]对湿周上有多种糙率的渠道开展研究,推导出了综合糙率计算公式;张红岐[10]借助河套灌区多年的试验数据通过拟合的方式得出了不同衬砌材料组成的复合渠道的糙率系数计算公式。但是,模袋混凝土衬砌技术由于引进时间较短,仍属于新工艺、新技术,设计标准中尚未给出模袋混凝土衬砌渠道糙率系数的取值范围,也没有模袋混凝土复合断面衬砌渠道糙率系数的计算公式,实际工程应用中设计人员一般根据经验选用,误差较大。糙率系数是渠道断面设计中重要的技术参数之一,是用来衡量渠道边壁的凹凸程度和壁面粗糙程度对水流流动产生影响的计算系数,它直接影响渠道的工程量和实际输水效果[11]。在水力计算中,糙率系数取值的准确性对工程造价和安全有很大影响[12]。南水北调中线工程的北京干线经评估,糙率系数值每下降0.001,工程投资就会减少数亿元[13]。由此可见,在大型渠道输水工程建设中,糙率系数取值的大小,对工程量和工程造价的影响是巨大的。通过原型观测对衬砌防渗渠道的糙率系数开展研究是一种行之有效的手段。孟立敏[14]利用曼宁公式计算不同水深和流量条件下不同衬砌材料组成的复合渠道糙率系数,并利用宁夏引黄灌区复合渠道糙率系数的原型观测结果对计算公式进行了验证;张建斌等[15]在宁夏引黄灌区选取了具有代表性的11条不同流量级别的骨干渠道,开展衬砌渠道原型糙率观测试验,提出了不同衬砌材料的建议取值。虽然国内外对渠道糙率系数有了很多的研究,但是对于边坡采用模袋混凝土衬砌、渠底采用砂砾石砌护的模袋混凝土复合断面衬砌渠道的原型观测试验尚未见到文献资料。本文在河套灌区什巴分干渠和建设二分干渠选取模袋混凝土复合断面衬砌渠道试验渠段,开展原型观测试验,测定复合断面模袋混凝土衬砌渠道糙率系数,并进行误差分析,对模袋混凝土技术在渠道衬砌与防渗工程中的进一步应用具有重要意义。
1 原型观测试验
1.1 测试渠段的选择
进行衬砌渠道糙率系数的原型观测试验时,观测断面的选取特别重要。本次试验分别在河套灌区什巴分干渠(0+200~2+216)、建设二分干渠(1+910~3+040)布设测流段面,测流渠段要求满足以下条件:(1)测流面所在渠段顺直、水流均匀平稳,均匀无回流,测流面与水流方向垂直;(2)测桥架设前后1 km内均无水闸、坎等建筑物,不受上游建筑物泄流和下游建筑物回水影响;(3)测流段内无冲刷淤积;(4)测流段所处区域交通通畅,便于仪器设施等运送、安装。
1.2 试验渠段基本情况
什巴分干渠从丰济干渠第二节制闸引水,分干渠全长32.1 km,设计引水流量为22.0 m3·s-1,加大流量26.0 m3·s-1。渠道防渗衬砌采用梯形断面,渠道两边坡铺设15 cm厚模袋混凝土防渗衬砌,混凝土强度等级为C25、抗冻等级为F200、抗渗等级为W6, 底部为经平整后的砂砾石。什巴分干渠试验渠段(0+200~2+216)长度2.016 km。
建设二分干渠开口于乌兰布和灌域一干渠第一节制闸,全长31.98 km,设计流量为15 m3·s-1,加大流量18 m3·s-1。渠道防渗衬砌采用梯形断面,渠道两边坡铺设15 cm厚模袋混凝土防渗衬砌,混凝土强度等级为C25、抗冻等级为F200、抗渗等级为W6,底部为经平整后的砂砾石。建设二分干渠试验渠段(1+910~3+040)长度1.130 km。
测流断面尺寸及断面水力参数见表1,断面结构见图1。

表1 测流断面尺寸及水力参数表

H:渠深(m);h:设计水深(m);B:渠口宽(m);b:渠底宽(m);m1:右岸边坡系数;m2:左岸边坡系数H:Ditch depth(m) ;h:Design water depth(m) ;B:Channel width bottom(m); b:Width of canal slope(m);m1:Coefficient of right bank ;m2:Slope coefficient of left bank图1 渠道测流断面结构示意图Fig.1 Channel flow measurement schematic cross-sectional structure
1.3 观测内容及方法
结合试验渠段断面形式和衬砌结构,现场测量内容包括渠道断面尺寸、断面水深、断面流量等。渠道断面尺寸采用钢卷尺和水准仪测量;渠底高程测量采用精度为1 mm的DS1型水准仪;流量采用测速范围在0.2~3.5 m·s-1,精度为1.5%的SL68型旋杯式流速仪测量平均流速,计算出断面流量。流速采用精测法测量[16],在观测断面上布设7条测线,根据水深情况确定垂线上测点个数,用面积-流速法处理测定结果,即用流速仪分别测出由测速垂线分隔的若干部分面积的部分平均流速,然后乘以部分过水断面面积,求得该部分流量,再计算其代数和得出断面流量,由断面流量与过水断面总面积求得断面平均流速;水深用精密水准仪和精度为1 mm的水尺测量。流量和水深测量时结合灌区灌溉用水情况,什巴分干渠测试时间为2017年10月19日—10月28日,水温为3℃;建设二分干渠测试时间为2017年10月29日—11月4日,水温为2℃。每组数据上下游断面同时测量。
2 结果与分析
2.1 糙率系数计算公式
测定渠段水流假定为恒定非均匀流,渠道上下游断面能量守恒,其基本公式为:
(1)
其中
(2)
(3)
(4)
由(1)~(4)式可得,恒定非均匀流渠道糙率系数的计算公式为:
(5)
式中,n为渠道糙率系数;Q为流量;h1为上断面水深,h2为下断面水深;A1为上断面面积,A2为下断面面积;L为渠道长度,g为重力加速度,i为底坡。
其中
(6)
2.2 原型观测结果
根据观测渠段断面尺寸、什巴分干渠测得的水深与流量,利用式(5)就可以计算出观测渠道的糙率系数。原型观测数据及糙率系数计算结果见表2。
由表2可得,什巴分干渠糙率系数最大值为0.0267,糙率系数最小值为0.0251,平均值为0.0259。建设二分干渠糙率系数最大值为0.0279,糙率系数最小值为0.0264,平均值为0.0272。什巴分干渠和建设二分干渠模袋混凝土复合断面衬砌渠道糙率系数范围为0.0251~0.0279,平均值为0.0265。

表2 原型观测数据及糙率系数计算结果
3 糙率系数测定的误差分析
3.1 糙率系数测定误差与水力测量误差的函数关系
在渠道糙率系数原型观测过程中,由于仪器精度及人为操作等问题,测得的流量、水深等水力参数存在一定误差,由此产生的误差会导致测定的糙率系数产生误差。渠道糙率系数试验中,需要测量上、下游断面面积A1、A2,渠底比降i,渠道长度L,渠道流量Q,上下游水深h1、h2等参数。渠道断面面积、渠底比降、渠道长度采用精密水准仪和钢尺测量,精度高、误差小,对糙率系数测定结果影响较小;流量和水深测量采用SL68型旋杯式流速仪和水尺,由于渠道断面流速分布不均,水面波动等影响,流量和水深的测量误差较大,对糙率系数测定结果影响较大。因此,糙率系数原型观测试验结果产生误差的主要影响因素为流量和水深。因此,为了分析模袋混凝土复合衬砌渠道糙率系数测定的误差,建立了观测断面水力 测量误差与渠道糙率误差之间的函数关系。
当测得渠道断面流量与水深时,可以用公式(5)计算渠道的糙率系数。由于流量和水深测量值存在误差,获得的糙率值也存在误差[17]。假设流量测量误差为ΔQ,上断面水深误差为Δh1,下断面水深误差为Δh2,则糙率误差的数学描述为:
(7)
式中,Δn=nr-n,Δh1=h1r-h1,Δh2=h2r-h2下标r为准确值,Q、h1、h2为测量值;∂n/∂Q、∂n/∂h1、∂n/∂h2是对(5)式分别求Q、h1、h2的偏导数。
对(5)式分别求偏导数可得:
(8)
(9)
(10)
其中:
(11)
(12)
(13)
(14)

(15)
(16)
将算得的∂n/∂Q、∂n/∂h1、∂n/∂h2代入式(7),可得渠道糙率误差。在测量设备误差给定情况下,渠道糙率最大误差是:
(17)
或者
|Δn|max≤|ΔnQ|+|Δnh1|+|Δnh2|
(18)
其中,ΔnQ=(∂n/∂Q)×ΔQ为糙率的流量测量误差分量,Δnh1=(∂n/∂h1)×Δh1为糙率的上断面水深测量误差分量,Δnh2=(∂n/∂h2)×Δh2为糙率的下断面水深测量误差分量。从公式(17)或(18)可以看出,只要已知流量和水深的水力参数测量误差,计算出流量测量误差分量和水深测量误差分量,就可以计算得到渠道糙率系数测定的误差。
3.2 糙率测定误差计算与分析
对什巴分干渠和建设二分干渠试验渠段糙率系数测定值进行误差计算。因为观测流量用的SL68型旋杯式流速仪测速范围在0.2~3.5 m·s-1,精度为1.5%,测水深用的精密水准仪、水尺精度为1 mm。故分别计算ΔQ/Q=1%、Δh=0.5 mm,ΔQ/Q=1.5%、Δh=1 mm条件下测流断面的测定误差。计算结果见表3和表4,渠道糙率随流量变化的误差曲线图见图2。

表3 什巴分干渠、建设二分干渠糙率的误差(ΔQ/Q=1%、Δh=0.5 mm)


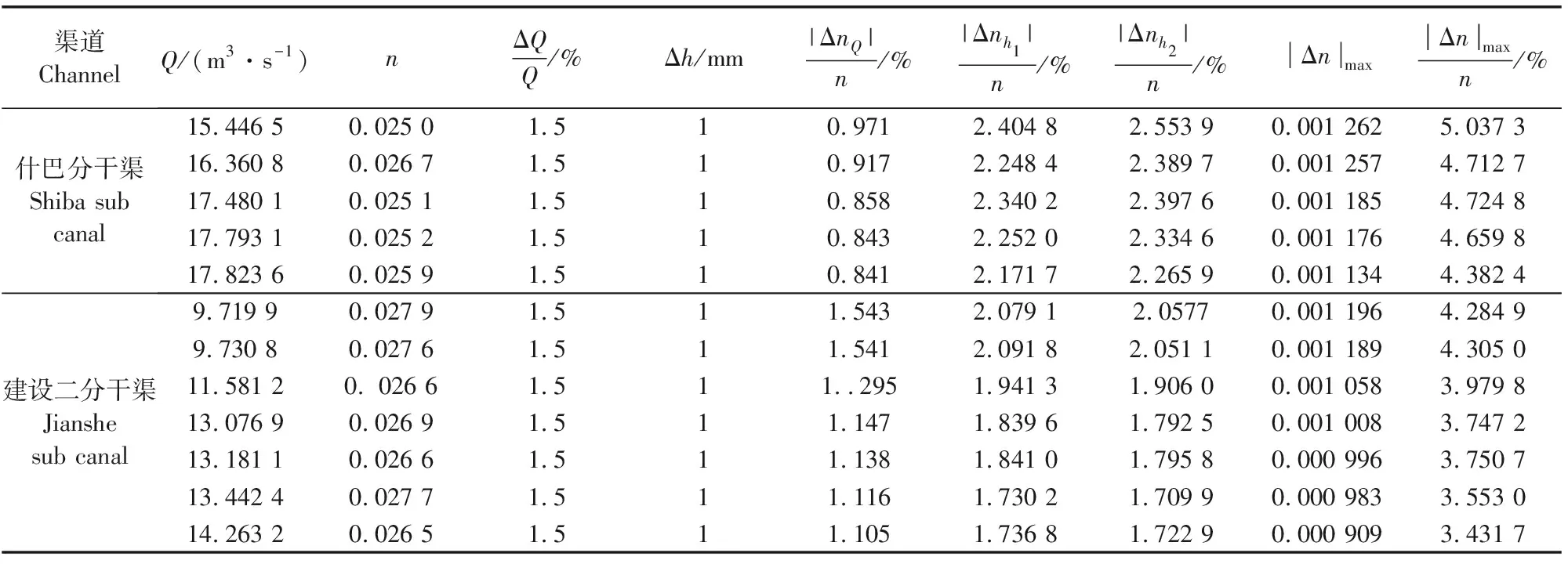
表4 什巴分干渠、建设二分干渠糙率的误差(ΔQ/Q=1.5%、Δh=1 mm)

图2 渠道糙率误差曲线Fig.2 Error curve of channel roughness
从表3和表4可以看出,测量水深、流量过程中,微小的水力测量误差可能产生较大的渠道糙率测定误差,经计算,什巴分干渠、建设二分干渠原型观测的糙率误差最大可达5.037%。由表3、表4和图2可以看出,引起渠道糙率误差的关键因素是糙率的水深误差分量|Δnh|/n,且上、下游水深误差分量近似相等,即|Δnh1|/n≈|Δnh2|/n,当建设二分干渠的流量为9.179 9 m3·s-1时,测量误差最大为1.543%,此时上、下游水深测量误差分别为2.0791%、2.0577%;当什巴分干渠的流量15.4465 m3·s-1时,测量误差最大为0.971%,此时上、下游水深测量误差分别为2.404 8%、2.553 9%,水深误差大小近似相等,但均大于流量测量误差,糙率测定的流量误差分量|ΔnQ|/n很小且稳定,说明本次试验观测流量用的SL68型旋杯式流速仪工作稳定,试验测得的数据准确、可靠。
由图2可看出,最大相对误差近似等于上下游水深测量误差之和,即|Δn|max/n≈|Δnh1|/n+|Δnh2|/n,因此,本次试验误差主要来源于测量水深读水尺时产生的误差,且水深误差分量随着过水流量的增大而减小,对同一渠道而言,渠道水深会随着断面流量的增大而增大,随着渠道水深的增大,读水尺产生误差所占比例变小,因此对同一渠道而言,糙率的水深误差分量随着断面流量的增大而减小,最大误差可达2.554%,从而引起的最大绝对误差可达5.037%。因此,建议今后测量时,采用更高精度的水深测量仪器,可有效减小渠道糙率测定误差。
4 结 论
1)对模袋混凝土护坡、砂砾石护底的复合断面衬砌渠道开展了糙率原型观测试验,引水流量为9.7~20 m3·s-1。现场观测计算了不同流量下什巴分干渠、建设二分干渠模袋混凝土复合断面衬砌渠道糙率系数范围为0.025 1~0.027 9,平均糙率为0.026 5。
2)通过渠道水力测量误差对渠道糙率测定影响的研究,建立了水力测量误差与渠道糙率误差之间的函数关系,计算分析了什巴分干渠、建设二分干渠实测流量、水深产生的糙率计算误差,计算得到本次原型观测糙率测定最大误差为5.037%。
3)通过误差分析发现,流量测量误差很小,本次试验观测流量用的SL68型旋杯式流速仪工作稳定,试验测得的数据准确、可靠。水深测量误差偏大,最大可达2.254%。最大相对误差近似等于上下游水深测量误差之和,即|Δn|max/n≈|Δnh1|/n+|Δnh2|/n,建议以后进行原型观测试验,水深等应采用精度更高的仪器测量,最大化减小测量误差对糙率系数计算的影响。

