波状粗糙壁模型流动的壁面热流和阻力关联关系的数值研究

李玉川，鲍 麟

(中国科学院大学工程科学学院， 北京 100049)(2018年5月9日收稿； 2018年5月28日收修改稿)

非光滑表面的高速流动传热规律既是一个基础问题，也是航天工程领域广泛关注和研究的课题。以再入式航天飞船为例，其再入行星大气层时速度可高达20～30倍声速，相应产生高达数千K的高温，为使飞行器免受高温损坏，需采用烧蚀热防护技术，即在其表面涂上反应潜热高的热防护材料，依靠高温烧蚀过程，带走大量热流，以保护飞行器。由于典型材料烧蚀过程是非均匀的，会形成粗糙壁面，研究其气动加热规律成为航天工程中的重要问题之一。从20世纪70年代以来，以美国PANT计划[1]为代表，针对粗糙壁面热流开展了大量研究，一是利用实验数据拟合得到若干经验公式计算粗糙壁面的热流，如Dirling[2]，Phinney[3]，Grabow[4]，二是用各种数值方法计算流场和粗糙壁面的热流，如Yang等[5]，李俊红等[6]。这些工作共同揭示影响粗糙壁面热流主要参数有雷诺数、边界层厚度以及等效粗糙元高度等，为工程设计提供了重要理论基础。

由于前人的粗糙壁研究源于传统的大钝头式再入飞行器，其波阻远大于摩擦阻力，因此这些研究大多只关心粗糙壁的热流，而极少有对摩阻的讨论。当前正在研制的下一代航天飞行器将具备大气层内高速巡航能力，多采用扁平化的乘波体等气动外形，其波阻大大减小，而表面摩阻所占比重极大地上升，最多可达30%以上[7]，因此，飞行器壁面流动的摩擦阻力研究越来越受到重视。另一方面，下一代飞行器将实现可重复使用功能，工程设计提出采用非烧蚀热防护系统，使飞行器气动外形保持不变。实际上，飞行器表面在极高温作用下，不可能完全不烧蚀，尤其是多次长时间飞行后，其壁面应当看作存在微烧蚀，即是微粗糙的。综合上述两方面，微粗糙表面在高速流动中的壁面摩擦和传热是当前值得研究的问题，对新型飞行器的气动布局以及热防护系统设计有应用价值。

回顾光滑平板层流边界层理论可知，壁面热流与摩阻由临近壁面的边界层特性决定，且它们之间存在雷诺比拟关系[8]，即壁面热流与摩阻是成正比的，沿着平板流动方向，其比值是一个常数，仅与来流马赫数Ma∞、壁面温度Tw、气体的Pr数和比热比γ有关。对微粗糙壁而言，高速气体流经非光滑表面时，不仅壁面摩阻与热流发生变化，此时雷诺比拟是否仍成立存在疑问，而且与一般低速流动不同，压强波动产生的波阻是超声速时特有的现象，热流又与波阻有什么关系，是需要讨论的问题。

本文基于OpenFOAM程序数值模拟波状粗糙壁面在高速来流中壁面阻力与热流，及其流场特征，结果发现简单雷诺比拟关系不适用于粗糙壁情况，应代之以壁面热流与阻力之间的比拟关系，并分析该比拟关系的主要影响参数。为了深入分析该问题中的基本规律，同时针对新型飞行器高空巡航的特点，本文计算仅考虑层流情况，流动介质是空气，且看作量热完全气体(即特定气体常数R=287 J/(kg·K)、比热比γ=1.4、Pr=0.72，以下不再说明)，但结果揭示出的流动规律和机理也可为进一步研究各类工程实际情况提供参考。

1 物理模型与数值方法

在实际问题中，粗糙壁面形状是极其复杂的，即使是微粗糙的壁面，也不易用较为简单的形状来描述。早期实验中为了对其进行刻画，通常采用在光滑表面上均布不同形状和尺寸的粗糙元来模拟粗糙壁面，而为了使这些不同形状大小和排布的粗糙壁面具有相同的度量特征，Nikuradse[9]提出等效砂砾粗糙度：排布着普通粗糙元的壁面热流，和紧密排布着高度为ks的半球(三维)或半圆(二维)粗糙元的表面的热流相同，那么ks即为此粗糙壁面的等砂砾粗糙度。Signal和Danberg[10]对普通粗糙元到等效砂砾粗糙度的映射关系做了改进，在工程中得到广泛应用。

等效砂砾粗糙度概念的提出启示我们，可以利用一种标准粗糙元模型等效地模拟实际粗糙壁面形状，以获得壁面热流变化的规律，那么不失一般性，本文选取正弦波状外形作为标准粗糙元模型。

图1 正弦波状粗糙壁面示意图Fig.1 Schematic diagram of the sinusoidal rough wall

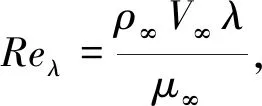
本文将利用数值计算方法求解上述粗糙壁模型的流动问题，主要探讨壁面热流、摩阻与压阻之间的关系，为此，引入定义无量纲壁面压强系数Cp、摩阻系数Cf与热流率系数Ch[8]：

(1)

已知高速气流的波状板流动的控制方程为二维定常、可压缩、黏性Navier-Stokes方程(以下简称N-S方程)：

(2)

有限体积法(finite volume methods，简称FVM)是计算流体力学中常用的数值方法，能够较好地保证流动的物理守恒性，因此，通常认为FVM类方法计算的壁面热流或摩阻的精度较高，本文利用OpenFOAM开源FVM程序，选取二阶Kurganov-Tadmor中心格式[11]求解上述N-S方程。具体格式详见文献[11]，在此不再赘述。重要的是该格式满足TVD特性和最大值原理，同时模拟流场具有高解析度，且与时间步长大小无关，因此，是一种理想的高速流动的计算格式。此程序的具体算例验证将在下一节中给出。

2 数值程序的验证

高速粗糙壁流动中压强梯度较大，这要求计算程序具有更高的流场解析度，为了验证本文采用的OpenFOAM程序的可靠性，首先，计算高马赫数光滑平板边界层前缘的黏性干扰区，并将壁面压强、摩阻与热流计算结果与已有的黏性干扰理论值作对比；其次，模拟超声速正弦波状板流动，在距离前缘充分远的区域，检验流场的数值解是否与理论上的二维定常超声速波形壁理论解一致；最后，对正弦波状板的高速流动计算结果的时间步长和网格密度无关性做检验。

首先，黏性干扰区算例的参数选取为Ma∞=8，单位雷诺数ReL=2×105m-1。依据Hayes和Probstein[12]得出的强干扰区摩阻和热流的分布公式为：

(3)

图2 平板黏性干扰区的Cf、Cp、Ch计算值与理论值的对比Fig.2 Comparison between the calculated and theoretical values of Cf, Cp， and Chalong a flat plate with viscous interference

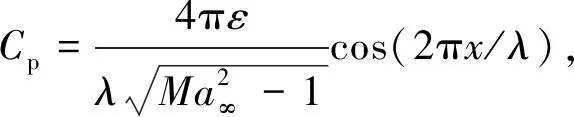
图3 无穷长波状板二维超声速流动的压强分布的理论值与计算值对比Fig.3 Comparison between the calculated and theoretical values of the pressure distribution along a wavy plate in 2-D supersonic flow

图4 不同计算参数下的波状板计算Ch、CQ、Cp曲线Fig.4 The calculated curves of Ch, CQ, and Cpalong the wavy plate with different calculation parameters

3 算例及分析

3.1 沿波状壁面的热流-阻力关联关系

(4)

(5)

CD=CDf+CDp，

(6)

(7)

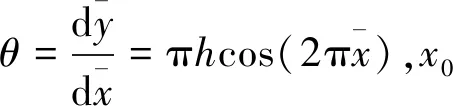
图5 h较小时CQ/CDf和CQ/CD随的分布(Ma∞=4，Reλ=2×104)Fig.5 Distributions of CQ/CDfand CQ/CDalong at the small hvalues (Ma∞=4，Reλ=2×104)

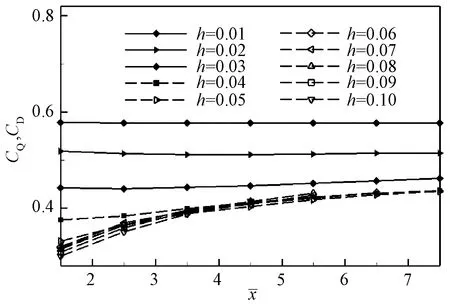
图6 不同h下的CQ/CD随的变化曲线(Ma∞=4，Reλ=2×104)Fig.6 Distribution of CQ/CDalong at various hvalues(Ma∞=4，Reλ=2×104)

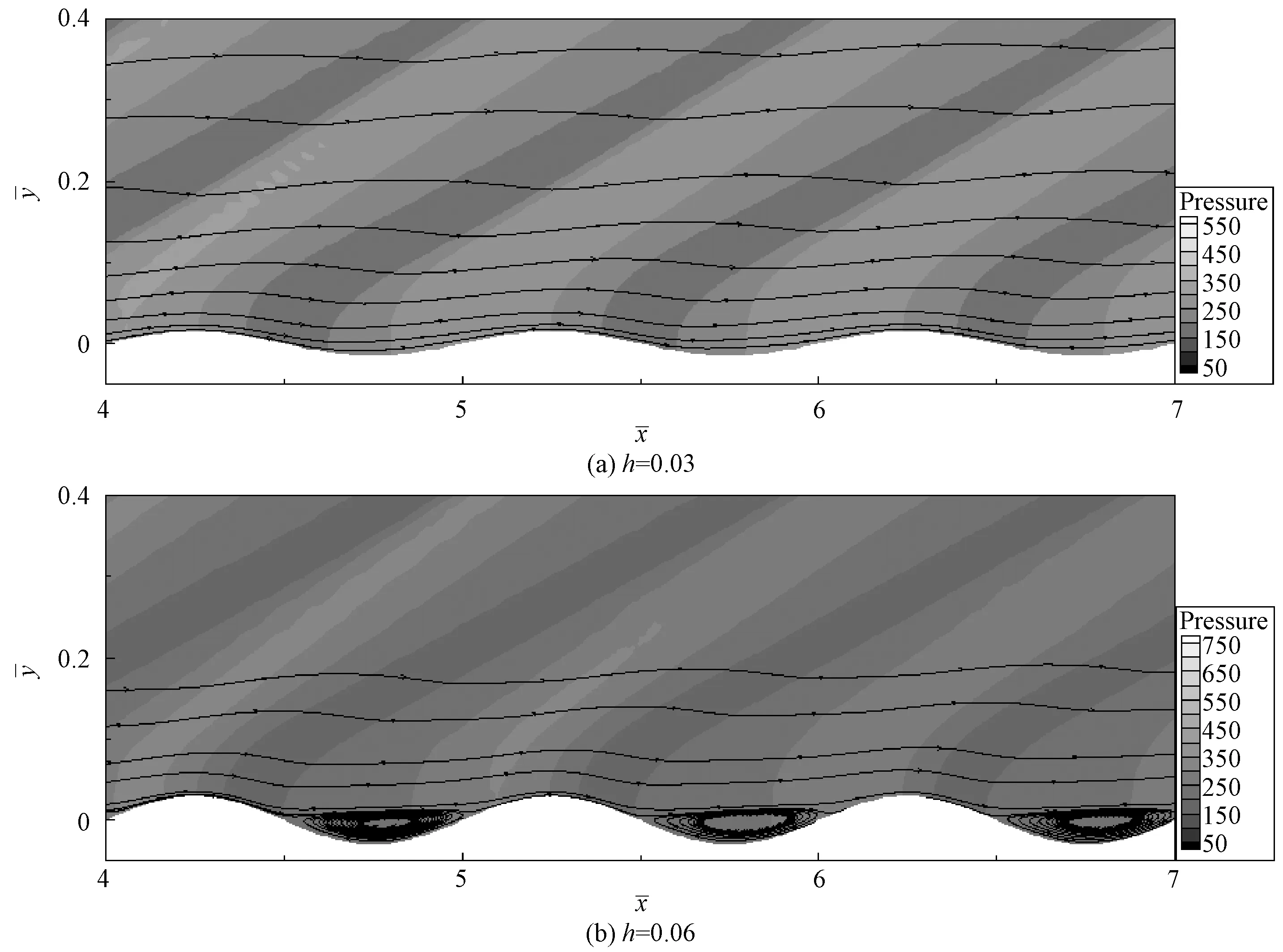
图7 h=0.03和h=0.06时壁面附近的流场图Fig.7 The flow field diagram near the wall when h=0.03 and 0.06

(8)

式中：Reθtr是以动量边界层厚度θ作为特征尺度的雷诺数；k为粗糙元尺度，即为本文中2ε。定性上讲，波状板的粗糙元尺度越大，位置离前缘越远，流动越趋向转捩乃至湍流。按本文设定的来流条件，设最大板长为x=1 m，即Rex约为105～106，则动量边界层厚度θ量级约为10-3m[16]，代入式(8)得到临界转捩粗糙元高度约为k≈0.01 m，即h=0.1。因此，本文仅讨论h<0.1时的波状板流动，将其看作层流流动，并且不包含出现局部紊乱流场时的情况，下面将集中探讨定常层流流动条件下的CQ/CD的具体变化规律。

3.2 热流-阻力关联关系的归一化

3.2.1 未分离的波状板流动

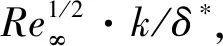
(9)

(10)

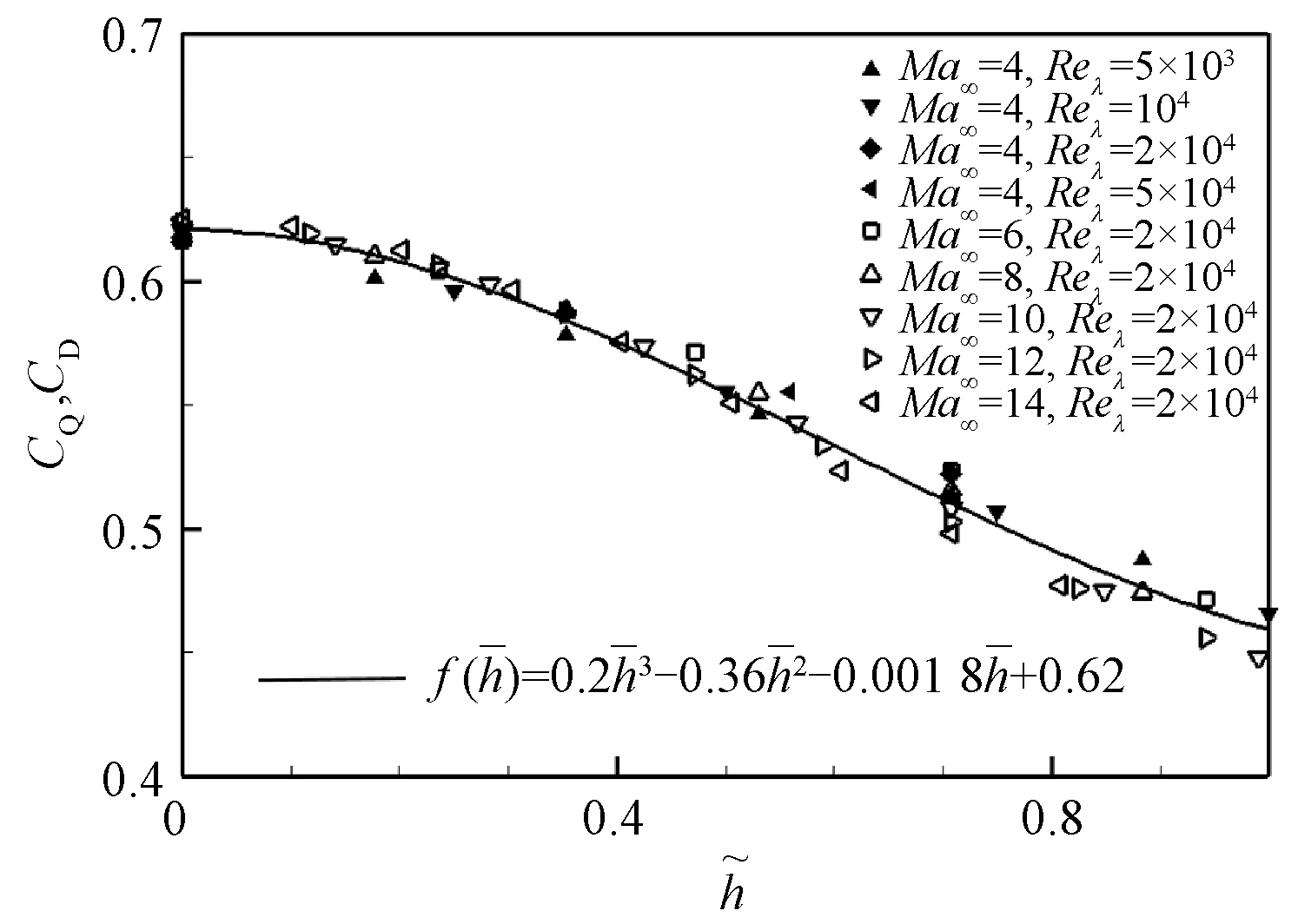
图8 不同Ma∞和Reλ下波状板附着流动CQ/CD随的变化规律Fig.8 The law of the CQ/CDchange with at different Ma∞and Reλvalues along the wavy plate in attached flow

式(10)由数值计算结果拟合得出，并无可对比的实验结果。在此仅从数值验证角度估算其误差范围：由第2节，壁面热流系数和摩阻系数最大偏差约为5%，而压强系数的最大偏差为10%，因此，可大致估计CQ/CD最大偏差约为15%～20%，可以供工程预研或工程估算时参考。

3.2.2 存在分离的波状板流动

(11)

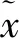
(12)

图9 不同Ma∞和Reλ下波状板分离流动的CQ/CD随等效位置的变化规律Fig.9 The law of the CQ/CDchange with the equivalent position at different Ma∞and Reλvalues along the wavy plate in separation flow

需要说明，虽然流动出现局部分离涡后，波状板上CQ/CD具有相似性规律，但流动在何处产生分离仍是一个难题。定性上讲，波状板来流Ma∞越低，Reλ越高，流动越容易分离，并且波状粗糙度越大，位置离前缘越远，流动越趋向于分离。然而暂时无法定量地给出流动开始分离的位置，这仍有待深入研究。

4 结论

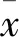
CQ/CD=

无论从前人历史研究的结论看，还是从波状粗糙板流动本身的分析角度看，定量确定流动开始分离的位置仍然是一个非常困难的问题，本文仅讨论壁面热流-阻力的关系，分离条件仍有待下一步深入研究。

本文得到王智慧副教授的诸多指导和启发，在具体工作中也得到博士生李贤冬、罗健的热心帮助，在此谨表感谢。