让学生找到解决问题的金钥匙
杨雪
数学是一门最基础的学科,人们的日常生活时时处处都离不开数学,而数学中解决问题方面的知识则是重中之重,它影响着学生数学素养和日常生活解决问题的能力。然而,在多年一线的教学实践中,笔者发现 “解决问题”一直困扰着学生,很多学生在每次的作业、考试中成为失分最多的题目,中下层次的学生尤甚,“解决问题”的知识对学生来说像“老鼠咬鸡蛋——无从下牙”。根据对学生失分现象分析,大体可以归结为以下几种原因:①不读题不审题,个别学生读题“走马观花,”只是略看几个数字就急于作答,题目要求要解决什么问题,不知道,不了解,结果只能出差错。②读题未能“咬文嚼字”读准字眼,无法正确把握题意。③未能弄清题目数量关系,颠倒是非黑白。造成这些答题错误,既有“学”的客观原因,更有“教”主观因素。因此,教师在课堂教学上,是否做到“授人以渔”非常重要。那么,如何才能提高学生解决问题的能力,提高学生答题的准确度和数学素养呢?笔者认为可从以下四方面去尝试。
一、咬文嚼字法
1.咬字辨析
对于在解决问题中的题,先让学生粗读一遍,大概知道题目表达的意思,再让学生细读,读懂每一句话,明白题目给出了什么,求的是什么,特别是对题目中关键的字眼,可用笔将这些关键的字眼圈出来,还可以通过提问的形式引导学生正确理解题意。
如“淘气家八月份用水14吨,比九月份多用了1/6,九月份用水多少吨?”学生往往把“比九月多了1/6”,读成“九月份用了1/6”,把“多”字读漏了便会改变题意,所以要求学生把“多”字圈出来,特别提醒,不要读漏。
又如“淘气正在读一本281页的故事书,不小心合上了,他记得刚读的连续两页页码之和是81,如果淘气每天读20页,剩下的几天能读完?”要求学生认真读题,理解每一句话的意思后,再提问学生“题目里知道什么?”“求什么?”“连续两页页码之和是81,你是怎样理解?”“两页页码分别是多少?”“剩下的页码数是多少?”“用什么方法来求出剩下的几天能读完?”通过多读详问,学生对题意的理解就容易多了。
2.换词理解
用具体的语言帮助学生理解名词术语和语言表达方式的不同。如“某地区总面积8000km2,其中有240km2的森林区,这个森林区的森林覆盖率是多少?”中,“覆盖率”这个词学生难以理解,老师可以引导学生把问题中的“森林覆盖率是多少”改成“森林区面积占总面积的百分之几”,去理解“覆盖率”的具体含义,然后延伸到生活中的“发芽率,出勤率,命中率……”加深理解。
二、数量剖析法
剖析数量关系是解决问题的关键。一般学生在解决问题时都没有习惯先找出数量关系,再列式。学生常常看见数字就列式计算,不知道所列的式子是否对错、是否符合题目的要求,所以,让学生养成解决每一道题时都要找出题中的数量关系,再列式解答。如“少年宫合唱队有84人,合唱队人数比舞蹈队的3倍多15人,舞蹈队有多少人?”这道题中“合唱队人数比舞蹈队的3倍多15人”是关键句,必须让学生读到理解然后把这句话转变成舞蹈队人数的3倍加上15人,正好等于合唱队的人数,再转化成数量关系:舞蹈队人数×3+15=合唱队人数。根据这个关系式就可以正确列出算式。又如“黄豆营养很丰富,其中蛋白质含量约占36℅,250克黄豆中,蛋白质约有多少克?”,“蛋白质含量约占36℅”表示蛋白质是黄豆的36℅。等量关系是:黄豆×36℅=蛋白质,学生只要把黄豆的250克写入等量关系里,就可以求出蛋白质的数量了。经过剖析数量关系,再引导学生用方程解决就轻而易举了。
三、示图理解法
数学是较为抽象的一门学科,学生对一些较为抽象的数学问题,就难于理解,教师可以借助示图通过直观教学帮助学生理解题意。
如“饲养小组养了9只白兔,5只黑兔,白兔比黑兔多多少只?”,可以结合教学图片(图1)引导学生分析:
白兔:○ ○ ○ ○ ○ ○ ○ ○ ○
黑兔:● ● ● ● ●
图1
题目已经知道什么,问什么?把白兔和黑兔一只对一只地对起来,看看对着的有几只(对着的有5只)。还有几只没有对着(4只),怎样求出白兔比黑兔多的只数呢?引导学生想出,从白兔的只数(9)减去和黑兔同样多的只数(5),剩下的就是白兔比黑兔多的只数,列式:9-5=4(只)。
线段图不仅可以直观地反映解决问题里的数量关系,也启发学生思维,而且可以通过画线段图的训练,调动学生思维的积极性,提高学生分析问题和解决问题的能力。
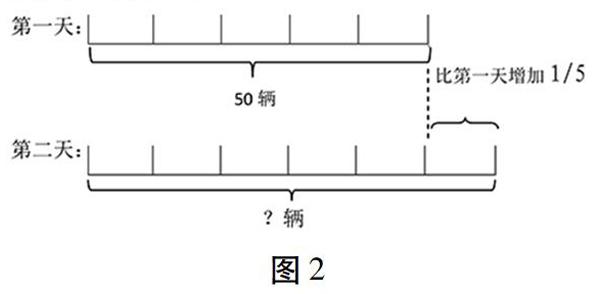
例如“第十一届动物车展,第一天成交50辆,第二天成交量比第一天增加了1/5。第二天成交量是多少辆?”把这题意画在线段图上(图2)。
这样学生可以清楚地看出:第二天比第一天增加的1/5,把第一天看作整體“1”,第二天的分率是(1+1/5),知整体“1”(50辆)。求第二天的成交量是多少?则列式为50×(1+1/5)。学生还可以容易看出:先算出比第二天增加的辆数50×1/5=10(辆),再加上第一天的50辆就是第二天的辆数。运用图示让学生理解题意、理清思路是有很大帮助的。
四、实物演示法
实物演示可以使数学形象化,数量关系具体化,学生对题目的理解更简单明了。如“一个圆柱形橡皮泥,底面积是12cm2,高是5cm,如果把它捏成同样底面大小的圆锥,这圆锥的高是多少”,遇上这种抽象的题目,学生的空间思维能力差,只能借助实物演示。拿一个底面积是12cm2,高是5cm,的橡皮泥或面团,在学生面前演示,捏成同样底面的大小的圆锥,学生看后悟出体积不变,高变了,而是变高,并量到是15cm,再通过思考和验证得到圆锥的高是与它等底等体积的圆柱的高的三倍,列式为:15×3=15(cm)。因而遇到抽象的题目可以利用实物演示来帮助理解。又如,“把一根200厘米的圆柱形木料,横截成两段,表面积比原来增加62.8平方厘米,这根圆柱形木料的体积是多少立方厘米”。学生对题目中的“横截成两段表面积比原来增加62.8平方厘米”很难理解,教师只能通过拿实物演示,帮助学生理解。拿一根圆柱形木料(或粉笔)把它竖起来200厘米就是圆柱的高,再理解“横截”,把木料横放着,然后切开,这样切开叫作“横截”。再让学生看一看,想一想,说一说什么增加了,什么不变。学生从实物中知道体积不变,表面积增加,增加了两个圆,也就是增加两个底面。再理解“表面积比原来增加62.8平方厘米”,其实增加62.8平方厘米就是增加两个底面的面积,拿62.8÷2就是一个底面积,再根据底面积×高=木料的体积。
责任编辑 黄博彦

