型钢活性粉末混凝土柱大偏压性能分析
卜良桃,秦 川
湖南大学土木工程学院,湖南长沙 410082
活性粉末混凝土(reactive powder concrete, RPC)是一种具有超高的抗压强度、较高的抗拉强度以及良好的耐久性[1]与冲击韧性[2]等优点的新型水泥基复合材料.普通高强混凝土的抗压强度一般在60~100 MPa,而RPC的抗压强度可高达100~200 MPa[3-4].目前,国内外对RPC的材料性能以及结构设计方面的应用进行了大量的理论分析与试验研究,并已在桥梁、轨道、核电、港口和结构加固等领域广泛运用[5-7].罗恺彦[8]通过型钢RPC的短柱推出试验,分析了型钢与RPC之间的黏结机理,建立了界面极限黏结力的计算公式,为型钢RPC结构计算理论的建立提供了试验依据.SHI等[9]通过22根钢筋RPC试件的大偏心受压试验,分析了配筋率、有无钢纤维等因素对试件承载力的影响,得出试件承载力与RPC强度基本呈线性关系的结论,建立了大偏心受压钢筋RPC柱极限荷载的简化计算方法.刘畅[10]通过无筋RPC短柱偏压试验,得到不同偏心率作用下的极限荷载.卜良桃等[11-12]研究了型钢RPC柱的轴压力学性能,通过试验发现型钢与RPC具有良好的协同工作能力,通过有限元模拟及理论计算,提出了轴压承载力计算公式.
目前,国内外对RPC的试验研究未考虑尺寸效应对受力性能的影响,研究对象基本为缩尺试件,且未涉及型钢RPC柱大偏心受压的力学性能.为此,本研究制作了6根截面尺寸为300 mm × 350 mm,高度为3 000 mm的足尺型钢RPC试件进行大偏压试验,试验表明将两者组合形成型钢RPC柱,能充分发挥两种材料的优势,在大偏心荷载作用下,其变形能力及极限承载力均高于普通型钢混凝土柱,故可作为竖向承载构件应用于重载结构中,并考虑受拉区RPC应力的贡献[13],计算出型钢RPC柱正截面的极限承载力,供工程设计参考.
1 试验概况
1.1 试件设计
本试验为足尺试验,以含钢率、初始偏心距e0为参数,设计了6根型钢RPC试件,各试件参数见表1.其中,e0为初始编心距;h为柱截面的高度.由于偏心距对型钢RPC柱的力学性能及破坏形态有较大影响,为保证试件均为大偏心受压破坏,经试算,设计了e0分别为0.5h和0.6h的试件.为研究含钢率对试件受压性能的影响,通过设置不同的型钢腹板及翼缘厚度改变试件的含钢率,且均满足合理含钢率的要求[14].各试件长度均为3 000 mm,截面尺寸b×h为300 mm×350 mm(b为截面的宽度),试验所用的型钢等级均为Q235,纵筋与箍筋等级均为HRB400,直径分别为12 mm和8 mm,在柱端部设置牛腿方便加载,试件详细尺寸及配筋如图1所示.

表1 试件设计参数
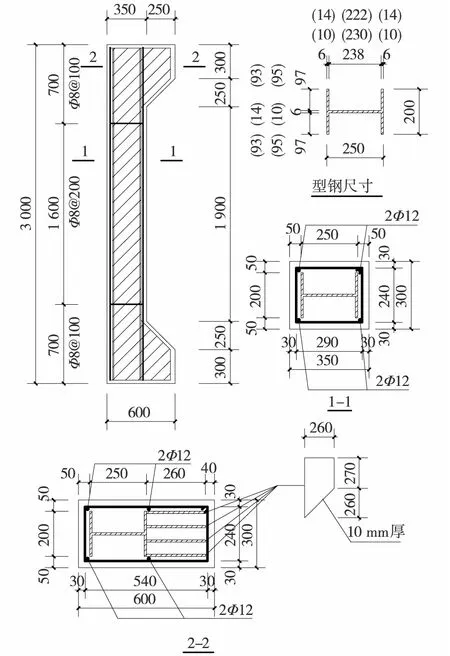
图1 试件尺寸及配筋详图(单位:mm)Fig.1 Dimensions and reinforcement details of specimens(unit:mm)
1.2 RPC力学性能

1.3 加载制度及观测方案
试件两端铰接,采用单刀铰支座进行偏心受压试验,试验装置简图见图2.为防止RPC局部受压破坏,在单刀铰支座与试件间垫一块厚度为30 mm的钢板.按照《混凝土结构试验方法标准》(GB/T 50152—2012)[17]的要求,在正式试验之前先进行几何对中,然后进行预加载,加载值不超过预估极限荷载的5%,确认各仪器仪表正常工作后正式加载.正式加载采用分级加载的方式,每级荷载增量为150 kN,持荷5 min.当荷载达到预估极限荷载的80%后,每级荷载增量为75 kN,持续加载至试件破坏.

图2 试验装置简图Fig.2 Schematic diagram of test device
试验的观测内容有试件侧向挠度、中部截面应变、裂缝产生及发展情况.试件的侧向挠度由沿柱高均匀分布的5个位移计测得,在试件中部截面沿截面高度布置应变片以测得其应变. 在试验进行时,用马克笔在试件上描出裂缝的位置及发展情况,并记录各条裂缝出现时的荷载以及裂缝宽度.
2 试验现象及结果
2.1 破坏过程及承载力
加载初期由于荷载较小,无明显试验现象,只是偶尔伴随着“滋滋滋”的钢纤维绷紧的声音,试件侧向挠度与荷载基本呈线性关系.当荷载增加至极限荷载40%左右时,试件中部附近受拉面出现了首条横向水平裂缝,RPC中的钢纤维被拔出或拉断,侧向挠度发展明显加快.随着荷载持续增大,受拉面横向水平裂缝增多,裂缝分布区域从试件中部向两侧逐渐扩大,并发展至侧面,试件中部附近受压侧RPC开始出现不规则裂缝.当荷载增至极限荷载时,试件受拉侧裂缝急剧发展,侧向挠度持续快速增长,试件中部附近受压侧RPC被压碎,保护层RPC局部剥落,受拉纵筋断裂,荷载开始下降,试件破坏.
试验结果表明,6根试件在偏心距分别为0.5h和0.6h的受压荷载下,均呈现典型的大偏心受压失效模式,且与普通钢筋混凝土柱类似.随着荷载的不断增加,受拉区RPC应力逐渐达到抗拉强度,试件产生受拉裂缝并不断发展,部分RPC退出工作,拉应力逐渐由型钢承担.试件的抗弯刚度减小,侧向弯曲变形速度加快,轴向压力在偏心方向产生的二阶弯矩增大,加速了RPC与型钢的应力发展.试件达到极限荷载时,部分保护层RPC被压碎,受压区与受拉区型钢翼缘、钢筋均屈服,受拉侧RPC出现一条水平主裂缝,型钢与RPC产生较大的滑移.缓慢卸载时,试件仍继续变形,型钢与钢筋进入强化阶段,水平主裂缝宽度渐增至约2 cm,裂缝处受拉纵筋被拉断.由于型钢与钢筋对核心区RPC的约束作用,导致RPC破坏基本发生在保护层区域,核心区域RPC较为完整,因此,试件仍具有较高的残余荷载,约为极限荷载约70%.
各试件的开裂荷载(Ncr)及极限荷载(Nu)见表2.偏心距分别为0.5h和0.6h的试件开裂荷载,与极限荷载的比值平均值分别为40.56%和36.36%,高于普通型钢混凝土试件[18],主要原因是RPC中掺入了钢纤维,具有较高的抗拉强度,能有效延缓试件开裂.由表2可知,试件的极限承载力随含钢率的增大而提高,随偏心距的增大而降低.
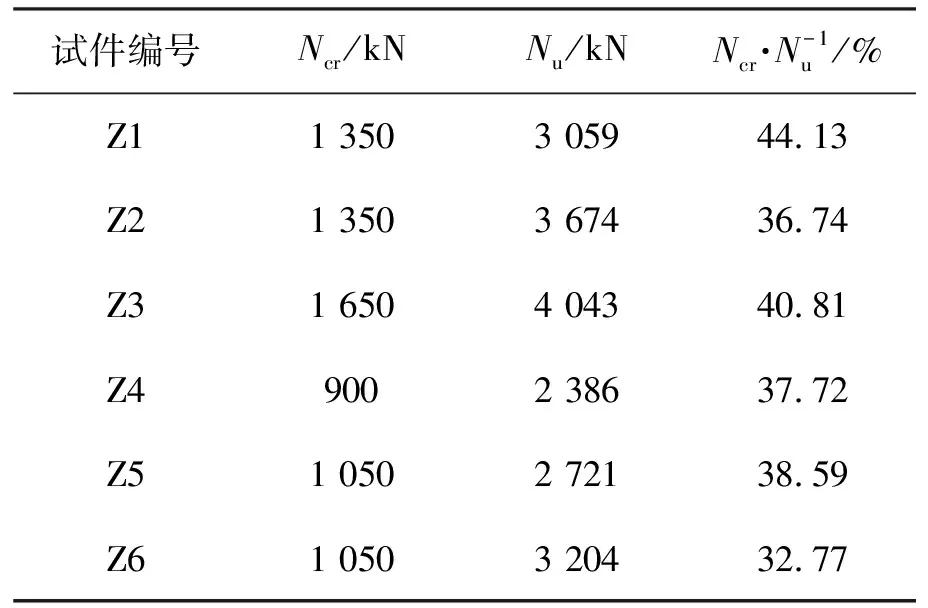
表2 试件开裂荷载及极限荷载
2.2 侧向挠曲分析
各试件侧向挠度曲线如图3所示.试件的侧向挠度沿柱高对称分布,且基本符合半波正弦曲线.当加载至开裂荷载后,裂缝截面RPC逐渐退出工作,试件抗弯刚度明显减小,侧向挠度增长加快,不再与荷载呈线性变化.由于试件均为大偏心受压破坏,达到极限荷载时曲率基本一致,故各试件达到极限荷载时的侧向挠度基本相同.试件的抗弯刚度随含钢率的增加而增大,随偏心距增大而减小.
2.3 应变分析
在试件中部侧面布置了5个应变片用于测得RPC应变沿截面高度的分布规律,最外侧测点距试件边缘25 mm,相邻两测点间距为75 mm.测得RPC的应变分布如图4所示.由图4可知,受压区RPC应变沿试件截面高度近似呈线性变化,基本符合平截面假定.因此,在进行承载力计算公式推导时仍然采用此假定.

图3 试件侧向变形曲线Fig.3 The deflection curves of specimens
3 承载力计算公式
3.1 弯矩增大系数
轴向压力在试件挠曲方向会产生二阶弯矩的现象,《混凝土结构设计规范》(GB 50010—2010)[19]中采用Cm-ηns法考虑此现象.其中,Cm为偏心距调节系数,对两端铰接的偏心受压柱,Cm取1.0;ηns为弯矩增大系数,根据平截面假定,由柱弯曲时的极限曲率推导得

图4 试件中部截面RPC应变分布Fig.4 Strain distribution of RPC in mid-span section
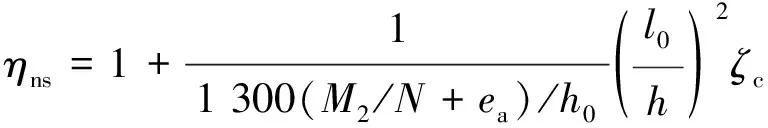
(1)
其中,M2为柱两端弯矩的较大值;N为轴力;ea为附加偏心距;h0为截面有效高度;l0为柱计算长度;截面曲率修正系数ζc=0.5fcA/N,A为柱截面面积, 当ζc计算值大于1.0时取1.0.
由于RPC较普通混凝土均质性好,强度离散性低,并且在实验室条件下,RPC施工质量较好,荷载位置准确,故在计算ηns与极限承载力时ea均取0. 弯矩增大至系数ηns的实测值与规范计算值对比见表3,由于RPC与普通混凝土相比具有更好的延性,故柱到达极限承载力时,RPC压应变更高,试件在极限状态下的曲率较大,试件中部侧向挠度更大,因此规范计算值均低于实测值.为充分考虑型钢RPC柱良好的变形能力,在ηns的推导过程中将混凝土极限压应变用RPC极限压应变εcu代替.

(2)
其中,εcu为RPC极限压应变;fy为纵筋抗拉强度;Es为纵筋弹性模量. 弯矩增大系数
(3)
将各值代入式(3),可得
(4)
式(4)计算的弯矩增大系数ηns与实测值对比见表3.计算值与实测值的平均比值为0.996,变异系数为6×10-3,与实测值吻合较好.
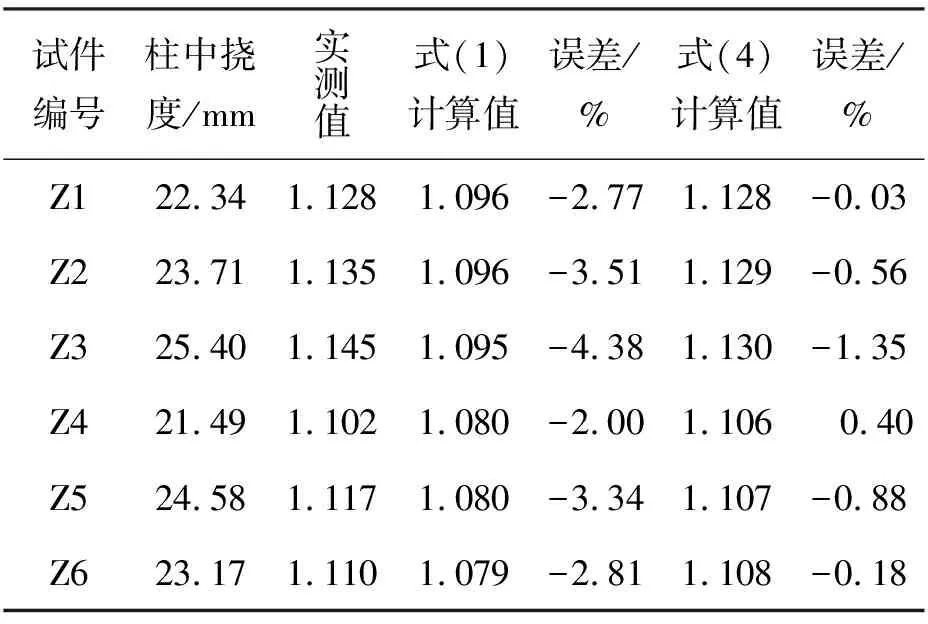
表3 弯矩增大系数的实测值与计算值
3.2 RPC等效矩形应力图系数
RPC受压应力-应变关系如下[13]:
(5)
其中,σ为RPC压应力;ε为RPC压应变;ε0为RPC峰值压应变.
根据文献[16]研究成果,ε0取3.36×10-3,εcu为4.76×10-3.为避免不必要的积分运算,将受压区RPC应力图简化为矩形应力图,简化原则为合力大小及作用点不变.根据RPC受压本构关系曲线、峰值压应变以及试件边缘RPC极限压应变,计算得到受压区等效矩形应力图的应力值与RPC轴心抗压强度比值α=0.95, 矩形应力图的受压区高度x与实际受压区高度x0的比值β=0.78.
由于RPC的轴心抗拉强度比普通混凝土高[20],试件受拉区RPC未开裂部分具有较大的拉应力,开裂部分由于钢纤维的作用,也存在一部分拉应力.故进行型钢RPC柱正截面承载力计算时,应考虑RPC拉应力的影响.由于受拉区RPC不符合平截面假定,且在型钢与钢筋的约束下,RPC抗拉强度能充分发挥,故与受压区RPC等效方法不同,在简化计算时,将RPC拉应力图等效为沿整个受拉区高度均匀分布的矩形应力图.等效后的RPC应力为kft. 其中,k为等效系数,可通过实测极限承载力反算得到.RPC受压区及受拉区的等效应力图如图5.

图5 RPC应力分布Fig.5 Stress distribution of RPC
3.3 极限承载力计算
钢筋及型钢的应力分布参考《组合结构设计规范》(JGJ 138—2016)[14],试件在极限状态下,钢筋与型钢翼缘均受压或受拉屈服,受压区边缘RPC达到极限压应变。为简化计算,假定中和轴以上型钢腹板均受压屈服,中和轴以下型钢腹板均受拉屈服,截面的应力分布见图6.根据力平衡条件可得式(6),各力对受拉区钢筋与型钢翼缘的合力作用点取矩可得式(7).

图6 极限状态下截面应力分布Fig.6 Cross section stress distribution in limit state

(6)
(7)

(8)
(9)
其中,δ1和δ2分别为型钢腹板上端、下端至截面上边缘的距离与h0的比值;tw为型钢腹板厚度.
当中和轴位于型钢上翼缘以上,即x<βδ1h0时,有
Naw=(δ2-δ1)twh0fa
(10)
(11)
当中和轴位于型钢下翼缘以下,即x<βδ2h0时,
Naw=(δ2-δ1)twh0fa
(12)
(13)
将极限承载力Nu代入式(6)和(7),可求得等效系数k与受压区高度x. 为保证受拉区型钢与纵筋屈服,x应满足
(14)
综合各试件等效系数k的计算结果,取k=0.4. 表4为各试件承载力的计算值.为方便比较,将不考虑RPC拉应力的作用,即取k=0的计算结果一并列入表中.从表4可见,如果不考虑RPC拉应力作用,计算承载力约为实测极限承载力的85%,计算结果偏于保守,未能充分发挥RPC的优越性能.考虑RPC拉应力作用后的计算值与实测值的平均比值为0.989,变异系数为1.6×10-2,与试验结果吻合良好,认为其具有较高的工程应用价值.

表4 试件承载力计算值1)
1)Nc1与Nc2分别表示k=0与k=0.4时的计算值.
4 结 论
综上研究可见,
1)型钢RPC足尺试件的大偏压破坏形态与普通型钢混凝土柱类似,达到极限荷载时的侧向挠度大于普通型钢混凝土柱,且仍具有较大的残余荷载,故该组合结构的变形能力较好.
2)型钢RPC大偏心受压柱具有较高的极限承载力,且随含钢率的增加而提高,随偏心距的增大而降低.
3)考虑PRC拉应力的贡献,建立了型钢RPC柱大偏压极限承载力计算公式.基于试验结果,RPC受拉区的等效矩形应力可取RPC轴心抗拉强度的0.4倍.

