二次通用旋转组合设计在假鹊肾树施肥量上的应用

包婷婷 郭昕 蔡传涛 黄春球 刘贵周

摘要：采用二次通用旋转组合设计，试验研究了氮、磷、钾3种常用肥料对幼龄期假鹊肾树生物量累积的影响，建立了施肥量与假鹊肾树生物量的回归方程。通过对试验结果进行方差分析，并对回归方程进行优化，得到假鹊肾树的较优施肥量和施肥配比。试验结果表明：当施肥量分别为氮肥（尿素，舍N 46.4%）20g/株，磷肥（过磷酸钙，含P2O512%）6g/株，钾肥（氯化钾，含K2O 60%）13g/株时，假鹋肾树生长较好。氮磷钾元素（N：P2O5：K2O）配比约为1.2：0.1：1。

关键词：假鹊肾树;二次通用旋转;氮肥;磷肥;钾肥

中图分类号：$567.1文献标识码：A 文章编号：1674-9944（2019）15-0097-05

1引言

假鹊肾树（Streblusindicus（Bur.）Corner）系桑科鹊肾树属多年生乔木，广泛分布于东南亚，尤其是中国云南西双版纳、广西、海南等亚热带中海拔地区。其树皮是一味常用傣药，称作“滑叶跌打”，常用于止血、治疗炎症和各种类风湿性疾病，故又有“止血树皮”之称。假鹊肾树自然资源分布稀少，又因是以树皮人药，不科学的采割以及生态环境的破坏导致其资源濒临枯竭，急需开展人工栽培研究。目前关于假鹊肾树的研究主要集中在药理药化方面，而没有人工栽培的相关报道。

合理施肥能有效促进药材生长、提高药材产量。通过确定肥料类型、施肥量，选择适宜施肥方法，最后达到最大的经济效益。施肥对苗木质量的影响主要表现在植株高度和地径的生长及生物量的积累。

为缓解假鹊肾树资源枯竭现状，本试验以幼龄假鹊肾树幼苗为材料，以氮肥、磷肥、钾肥为编码因子，采用二次通用旋转组合设计对假鹊肾树进行施肥处理，以假鹊肾树生物量为目标建立回归方程，并通过方差分析，对方程进行优化，最终得到幼龄假鹊肾树人工栽培较优的施肥方案。

2研究地区与方法

2.1试验地概况

试验地设在中国科学院西双版纳热带植物园，位于云南省西双版纳傣族自治州勐腊县勐仑镇（101°16E、21°55N，海拔570m）。由于地处东南亚热带北缘，属北热带季风气候区，年平均气温21.5℃，最热月（6月）平均气温25.5℃，最冷月（1月）平均气温14.8℃，10℃积温7860℃，终年无霜。一年中干湿季分明，年平均降雨量1557mm，其中雨季（6～10月）为1335mm，占全年的87%，干季（11月至次年5月）为202.0mm，仅占全年降雨量的13%。栽培用盆大小规格为：外口径32cm，底边长18.5cm，高21am，需营养土10L。供试土pH值为5.46，有机质含量13.51g/kg，全碳含量1.06g/kg，全氮含量1.06g/kg，全磷含量0.38g/kg，全钾含量8.44g/kg，水解性氮91mg/kg，有效磷12.04mg/kg，速效钾52mg/kg。

2.2试验材料

试验材料为假鹊肾树10个月龄幼苗，于2016年10月从野外采集种子在沙床培育，待长出3～4片真叶后移至营养袋，在营养袋培育至2017年8月移栽幼苗人盆。定植时测得株高为（27.88±0.36）em，基径为（2.51±0.55）mm，分枝数为（0.250±0.03）个。

2.3试验设计

本试验以盆栽苗期的假鹊肾树作为实验对象，以氮肥、磷肥、钾肥为试验编码因子，采用二次通用旋转组合设计进行栽培实验。根据预实验结果，综合考虑得出假鹊肾树幼苗合理施肥量的大致范围为：尿素O～32g/盆、氯化钾O～30g/盆、过磷酸钙O～18g/盆。设氮肥、磷肥和钾肥3个因素、五水平（表1），共20个处理（具体处理列于表2），每个处理5盆，重复3次。所有处理在同一环境内进行。

2017年8月定植时施基肥：0.34kg/盆，后期每隔3个月进行一次追肥。追肥为尿素（含N 46.4%）、过磷酸钙（含P2O512%）、氯化钾（含K2O 60%），共4次，根据西双版纳地区干雨季的特点，分别在2017年9月、2017年12月、2018年3月、2018年6月施肥，4次施肥量比例为2：3：3：2。每次施肥采用环施，将肥料均匀撒施后，覆土并立即浇水润湿表层。试验期间行统一的水份管理，保持土表微湿。

2.4生物量的测定

2018年10月在每个处理中随机选取4株假鹊肾树，将整个植株全部挖出洗净，然后放入烘箱内在60℃下烘至恒重（60～72h），用电子称测量其重量。

2.5统计分析

二次通用旋转组合设计的实验结果用杭州睿丰信息技术有限公司的DPS（Data Processing Systemv7.05）数据处理软件运行分析。 3结果与分析

3.1建立假鹊肾树生物量与氮、磷、钾施肥量的回归程

二次通用旋转组合实验方案及结果如表2所示。氮肥、磷肥和钾肥3个因素对假鹊肾树生物量相互作用所得方差分析结果见表3。

3.2主因子效应分析

回归方程的偏回归系数绝对值决定因子的重要程度，系數的正负表示因子效应作用的方向。因此，根据所得回归方程可以看出，假鹊肾树各施肥因素在试验取值范围内对其生物量干重影响大小依次为：X3（钾肥）>X2（磷肥）>X1（氮肥），其中x1与X3为正效应，X2为负效应。

3.3单因子效应分析

根据试验结果将单个施肥量因素对假鹊肾树生物量的影响进行效应分析。

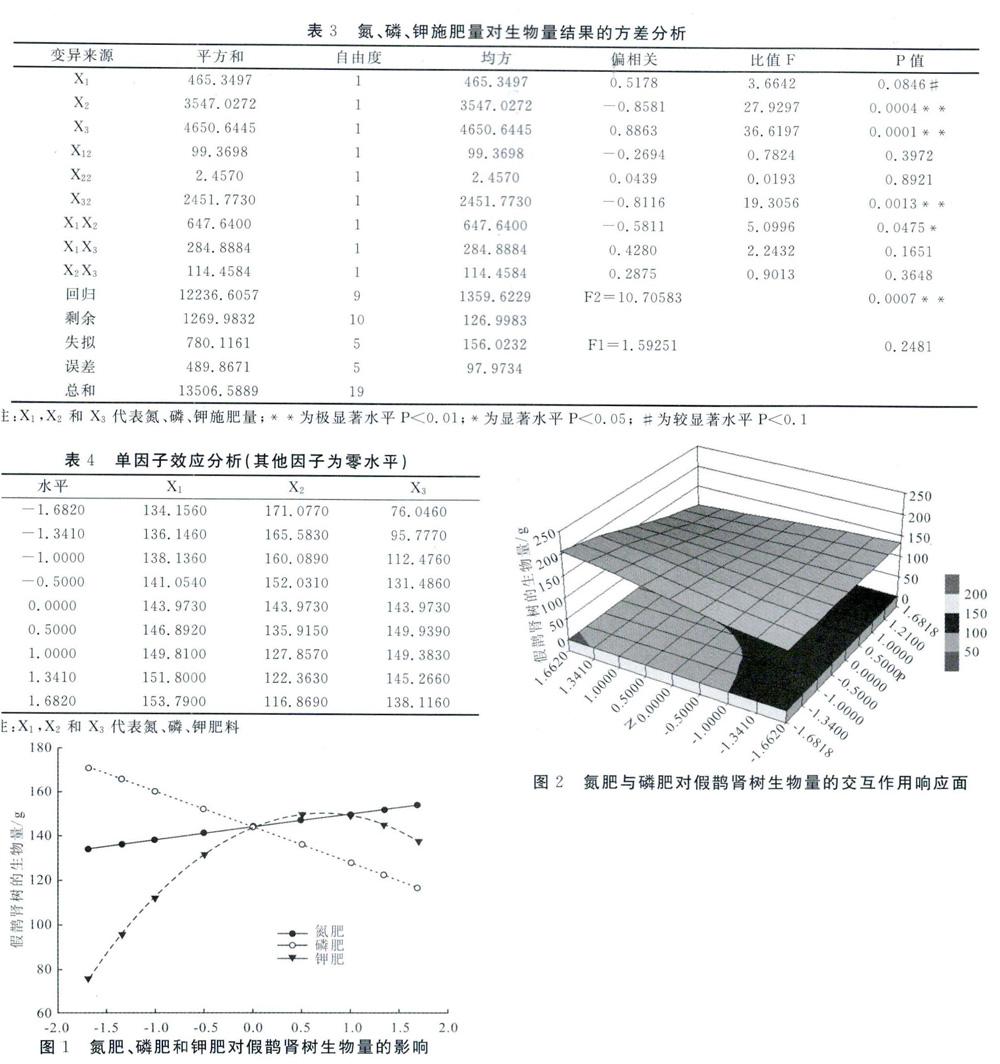
如图1所示，钾肥对假鹊肾树总生物量影响最大，其次是磷肥，氮肥对假鹊肾树总生物量影响最小。在-1.682～O水平（即钾肥施肥量在O～9g时）范围内，假鹊肾树生物量随着钾肥用量的增加而显著增加，随后生物量的变化趋于平缓，在0.5水平时生物量达到最高，钾肥施肥量为11.68g。在试验设计的氮肥水平范围内，生物量随着氮肥用量的增加而增加。氮肥对假鹊肾树生物量的影响在试验水平1.682时达到最高，此时氮肥施肥量是32g。磷肥对假鹊肾树生物量的影响在试验水平？1.682时（磷肥施肥量为0g）达到最高，且随着磷肥的增施，假鹊肾树生物量呈减少趋势。磷肥对假鹊肾树生物量的影响呈负效应。

综上，仅分析单因子效应时，将因素水平组合：X1=1.6820、X2=-1.6820、X3=1.0000用DPS数据软件进行运算，得出假鹊肾树生物量预测值为211.75g。

3.4互作效应分析

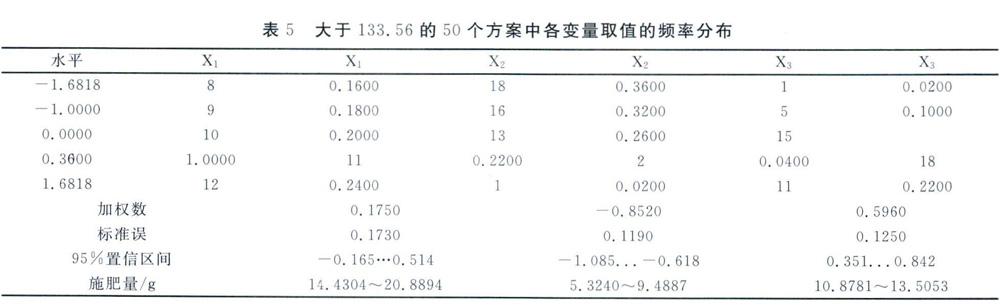
选取一个因素固定于零水平，考察另两个因素的交互作用，分别作图可以直观地分析各因子间的互作效应。本试验得出的回归方程中只有X1X2达到显著水平，因此仅对X1X2的交互作用进行分析，结果见图2。

由图2可知，随着氮肥量的增加以及磷肥量的减少，假鹊肾树总生物量呈现出不断增加且逐渐变快的趋势。在一定的氮肥施肥量下，假鹊肾树总生物量随着磷肥的增施而明显减少;在较高的磷肥施肥量下，升高氮肥施肥量假鹊肾树总生物量反而减小。因此，选定适宜的氮肥及磷肥施肥量和配比对提高假鹊肾树总生物量尤为重要。

3.5施肥方案的优化

由试验结果分析可知，很难从单因素效应和交互作用的结果分析中找到最佳施肥量，三元二次回归的数学函数不存在极值，因此采用频率分析法分析回归模型以找到最佳施肥方案。

由表5可知，在95%的置信区间假鹊肾树生物量大于133.56各变量的取值区间分别为-0.165…0.514，-1.085…-0.618，0.351…0.842，即每株假鹊肾树的氮肥施肥量为14.4304～20.8894g磷肥施肥量为5.3240～9.4887g钾肥施肥量为10.8781～13.5053g，在此范围内，结合实际栽培成本和效益，建议确定最佳施肥方案为：氮肥施肥量20g/株，磷肥施肥量为6g/株，钾肥施肥量为13g/株。

4讨论

假鹊肾树树皮是极其重要的一味止血药材，是云南红药胶囊和云南红药散的主要成分之一，年需求量大，目前尚未有人工栽培的研究，它的需肥特性尚未知。基于这个现状，本研究通过二次通用旋转组合设计以初步探究假鹊肾树幼龄树苗的施肥量。二次通用旋转组合设计是一种组合设计，为克服试验规模过于庞大，在因素空间中选择n类具有不同特点的点，把它们适当组合起来而形成试验。二次通用旋转组合设计可以在减少试验次数的同时获得较为准确的结果。该试验方法已经被研究人员广泛应用在优化、数据模型的模拟与预测中。因本试验数量庞大，为保证试验精度，提高试验效率，特选用此方法。有研究表明，过量或不足的氮磷钾的施用会抑制植物生长和干物质积累和分配，导致产量和质量下降。

从图1氮肥、磷肥和钾肥对假鹊肾树生物量的影响曲线可以看出，在试验设计的氮肥水平范围内，假鹊肾树生物量随着氮肥用量的增加一直在增加。氮肥对假鹊肾树生物量的影响在试验水平1.682时达到最高，此时氮肥施肥量是32g，说明在此次试验内，氮肥施肥量不一定达到假鹊肾树最大需求，需要进一步试验探究假鹊肾树最大氮肥施肥量。

在本研究中由回归模型得出的结果可知，假鹊肾树磷肥需求量极小，磷肥对假鹊肾树总生物量的影响在试验水平-1.682时达到最高，此时磷肥施肥量为O g，且随着磷肥的增施，假鹊肾树生物量呈减少趋势，磷肥对假鹊肾树生物量的影响呈负效应，可能是因为栽培土中的全磷已经能够满足假鹊肾树幼龄苗的生长，可再做进一步研究。相关研究试验结果表明，磷肥利用率随磷肥用量的减少而不断提高，磷肥减量是提高肥料养分利用效率的一种方式，因此在栽培假鹊肾树幼龄苗时可少施或不施磷肥。

在试验设计的钾肥水平范围内，假鹊肾树生物量随着鉀肥用量的增加呈现先增加后减少的趋势。当钾肥施肥量达到11.68g后，再增施钾肥，假鹊肾树总生物量开始下降，这可能是因为已经超过假鹊肾树对钾肥的最大需求，继续增施钾肥不仅不能增加产量还会导致产量降低，同时也浪费了肥料。为进一步验证以上结果，还可进一步开展假鹊肾树需肥特性的研究，比如假鹊肾树对氮磷钾肥料养分的利用率及其与环境效应的关系，进一步优化假鹊肾树的施肥量和施肥配比，提高产量，解决实际生产需求。

5结论

（1）试验选用二次通用旋转组合设计，以假鹊肾树总生物量为指标，以影响假鹊肾树生长的尿素（X1）、过磷酸钙（x2）、氯化钾（X3）三个因素为试验因子编码试验，得到了三元二次数学回归模型：