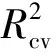基于神经网络的喹诺酮羧酸类衍生物活性研究

堵锡华,宋 明,李 靖,吴 琼,陈 艳,石春玲

(徐州工程学院 化学化工学院, 江苏 徐州 221018)

喹诺酮类衍生物属于人工合成抗菌药物,其中一部分甚至具有一定的抗肿瘤活性,能直接有效作用于细菌拓扑异构酶,对DNA旋转酶起到抑制阻碍作用,从而导致细菌DNA不可逆的破坏,迅速达到抗菌杀菌、抗肿瘤的作用[1],正是由于喹诺酮具有广谱抗菌、抗菌力强、疗效显著等优势,目前被广泛应用于人类和动物多种感染性疾病的治疗,但该类药物对人的中枢神经系统、消化系统、肌肉或骨骼等有一定毒性,对食用者健康会造成一定的危害[2],故为了提高该药物的使用效率,避免滥用误用,目前对该类药物的合成、分析检测、药理和临床合理应用等研究越来越受到研究工作者的重视。高留州等人[3]用芳腙类作为环丙沙星C-7哌嗪基的等排体,设计合成了15个喹诺酮羧酸类化合物,并对其抗菌抗肿瘤活性进行了分析研究,取得了令人满意的结果;杨家强等人[4]通过喹诺酮化合物与α-羟基膦酸酯拼合,设计合成了8个喹诺酮羧酸酯衍生物,通过测试表明,该类衍生物对肿瘤细胞有一定抑制作用;李凤丽[5]针对采用喹诺酮类抗菌药物与用其他药物进行治疗同样病症的患者进行了分析和对比,并对喹诺酮类抗菌药物具有的药理作用进行了评价,研究了在临床上的合理应用及其安全性。此外测定环境中残留此类药物的研究成果也较多[6-8]。但是，所有这些研究方法均需通过大量的实验,不但费时耗力,而且研究过程较长。为此，近年来利用计算机辅助药物设计的定量构效关系(QSAR)方法[9]对喹诺酮类衍生物进行研究逐渐受到重视,并有少量的相关研究成果[10-11],而利用神经网络法对喹诺酮类衍生物研究却较少。

神经网络是一个集计算机科学、化学、环境科学、建筑学、农学、食品科学等众多学科的一种前沿方法，具有交叉性，该方法在诸多领域已有广泛应用[12-14]。根据以前工作[15-17]基础,对48个喹诺酮羧酸衍生物的活性pIC50[11],按照文献方法[18-19]自编计算程序,计算了电性拓扑状态指数和电性距离矢量两类分子结构参数,用最佳变量子集回归法筛选了电性拓扑状态指数的E1和E8，电性距离矢量的M26，M32，M36和M81，共6种结构参数作为神经网络输入层神经元,将衍生物的活性作为输出层神经元,得到预测喹诺酮羧酸衍生物活性的神经网络QSAR模型,其总相关系数R=0.992 5,计算得到的活性预测值与文献实验值高度吻合,相对平均误差仅为0.87%。本研究解决了对新型药物需要进行大量实验费时耗资耗力、并需漫长等待的缺陷,具有预测精度高、快速简便的优点,而且利用模型可以设计活性高、毒性低的新型抗菌抗肿瘤药物分子,故在药物分子设计方面具有重要的现实意义。

1 衍生物分子结构及活性数据来源

喹诺酮羧酸衍生物母环结构见图1,48种喹诺酮羧酸衍生物分子相应基团见表1,活性数据pIC50(IC50的负对数)来源于前期研究[11]。

这48种喹诺酮羧酸衍生物分子的活性数据采用数据库文献中的相关数据,以pIC50作为分子的活性标度(IC50为达到50%抑制效果时抑制剂的浓度),使用Topomer CoMFA技术,对系列喹诺酮羧酸类衍生物进行三维构效关系的计算理论研究,建立了预测模型并进行了分子设计,取得了较好的结果。

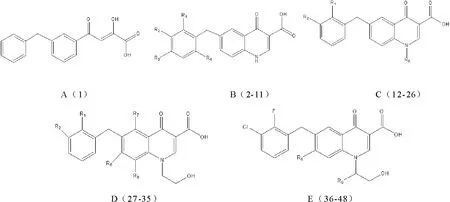
图1 喹诺酮羧酸衍生物的母体结构Fig.1 The matrix structure of quinolone carboxylic acid derivatives

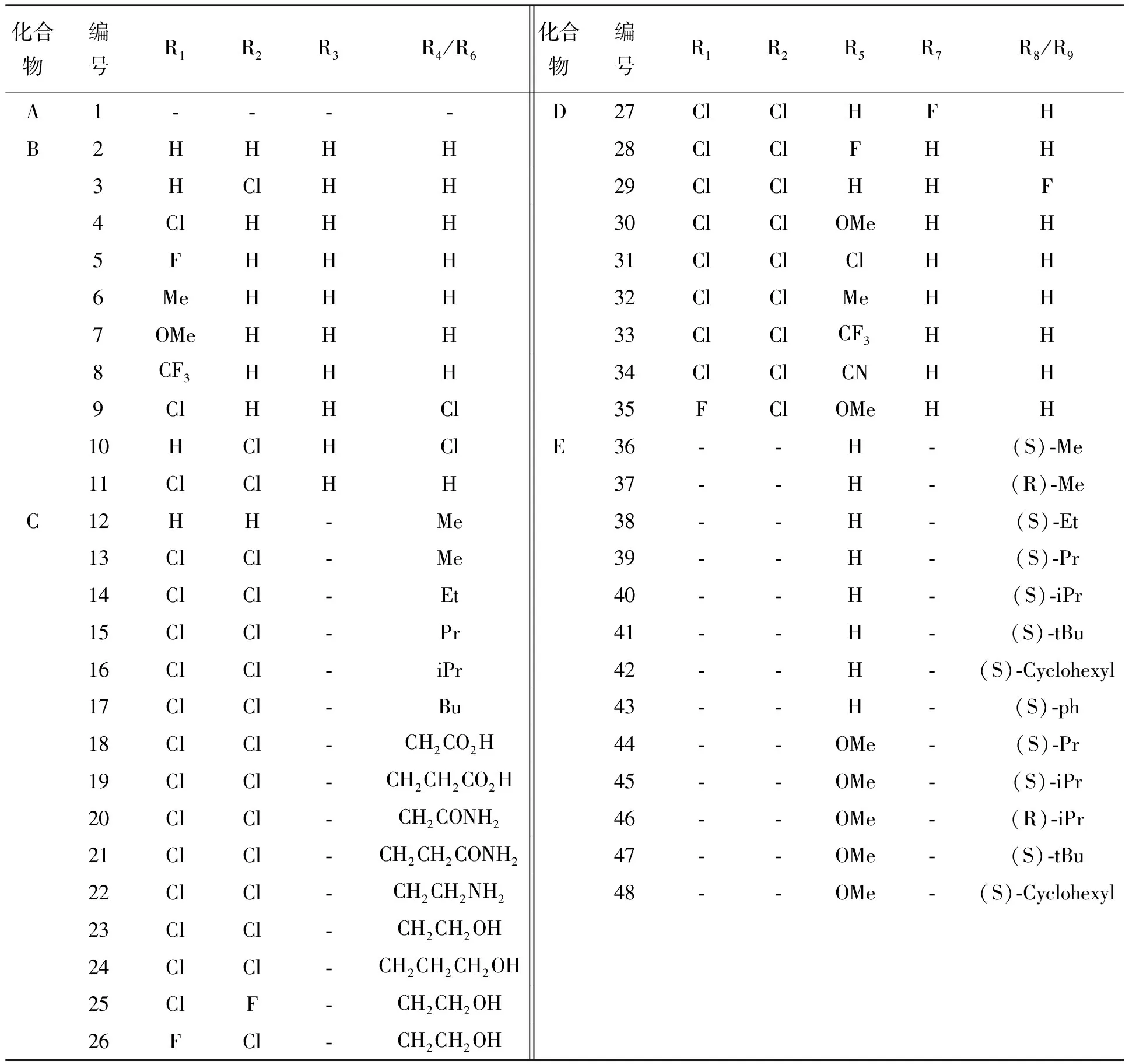
化合物编号R1R2R3R4/R6化合物编号R1R2R5 R7 R8/R9 A1----D27ClClH F H B2HHHH28ClClF H H 3HClHH29ClClH H F 4ClHHH30ClClOMe H H 5FHHH31ClClCl H H 6MeHHH32ClClMe H H 7OMeHHH33ClClCF3 H H 8CF3HHH34ClCl CN HH 9ClHHCl35FCl OMe HH 10HClHClE36-- H -(S)-Me 11ClClHH37-- H -(R)-Me C12HH-Me38-- H -(S)-Et 13ClCl-Me39--H -(S)-Pr 14ClCl-Et40-- H -(S)-iPr 15ClCl-Pr41--H -(S)-tBu 16ClCl-iPr42-- H -(S)-Cyclohexyl 17ClCl-Bu43--H -(S)-ph 18ClCl-CH2CO2H44-- OMe -(S)-Pr 19ClCl-CH2CH2CO2H45-- OMe -(S)-iPr 20ClCl-CH2CONH246--OMe -(R)-iPr 21ClCl-CH2CH2CONH247--OMe -(S)-tBu 22ClCl-CH2CH2NH248--OMe -(S)-Cyclohexyl 23ClCl-CH2CH2OH24ClCl-CH2CH2CH2OH25ClF-CH2CH2OH26FCl-CH2CH2OH

2 结构参数计算及变量的优化筛选

采用Chemoffice Chem3D画图软件，绘制前期研究[11]中所列48种喹诺酮羧酸衍生物的分子结构,根据Hall和Kier[20-21]提出的电性拓扑状态指数，刘树深等人[22]提出的电性距离矢量的定义方法,在Matlab中调用画好的结构,计算得到电性拓扑状态指数的46个、电性距离矢量的91个,两类结构参数共137个,去除两类137个参数中全部为0的数组,剩余的数组用最佳变量子集回归方法优化筛选,所得结果见表2。

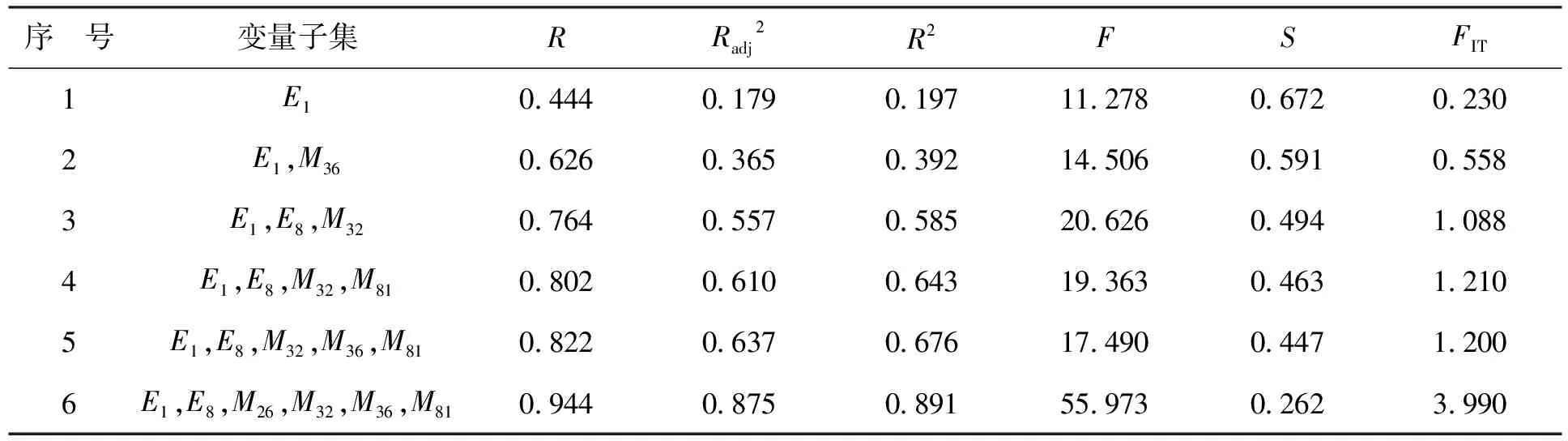
表2 pIC50与参数的最佳变量子集回归结果Tab.2 The results of parameters and pIC50 of quinolone carboxylic acid derivatives with best subsets regression

表中R，Radj2，R2，S，F，FIT分别为相关系数、调整的判定系数、决定系数、Fischer检验值、标准误差、Kubinyi函数

表2中FIT的计算方程式[23]为

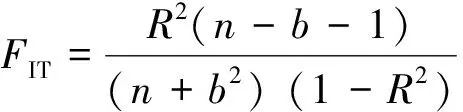
(1)

式(1)中n为喹诺酮羧酸衍生物分子的个数,b为建立模型使用的变量数,R2为建立模型的决定系数。

当选择两类结构参数中的E1，E8，M26，M32，M36，M81共6个参数时,活性pIC50与结构参数之间的相关性最好、标准误差也最小,这48种喹诺酮羧酸衍生物的结构参数如表3。

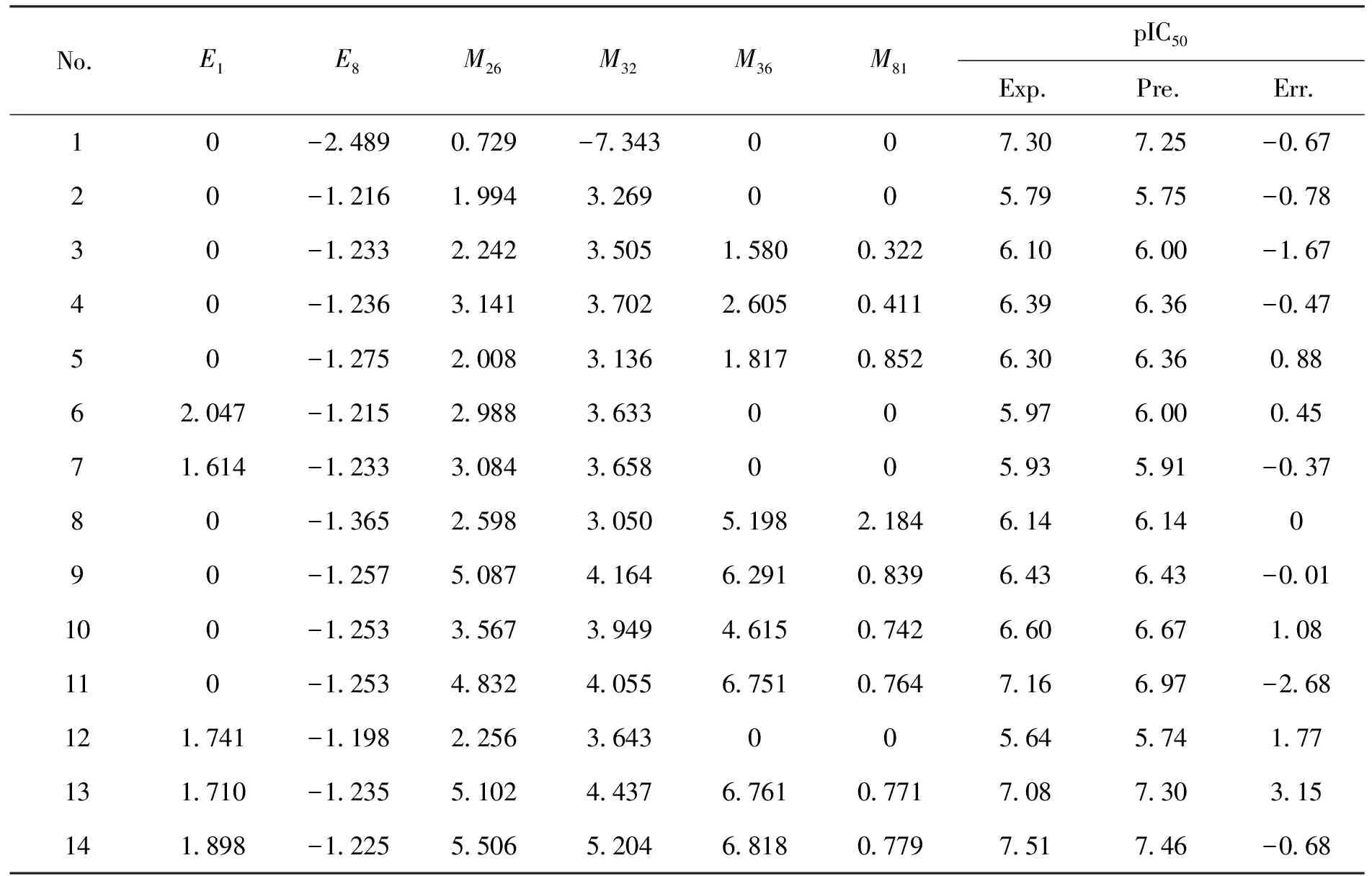
表3 喹诺酮羧酸衍生物的6种结构参数Tab.3 Six structural parameters of quinolone carboxylic acid derivatives

续表3

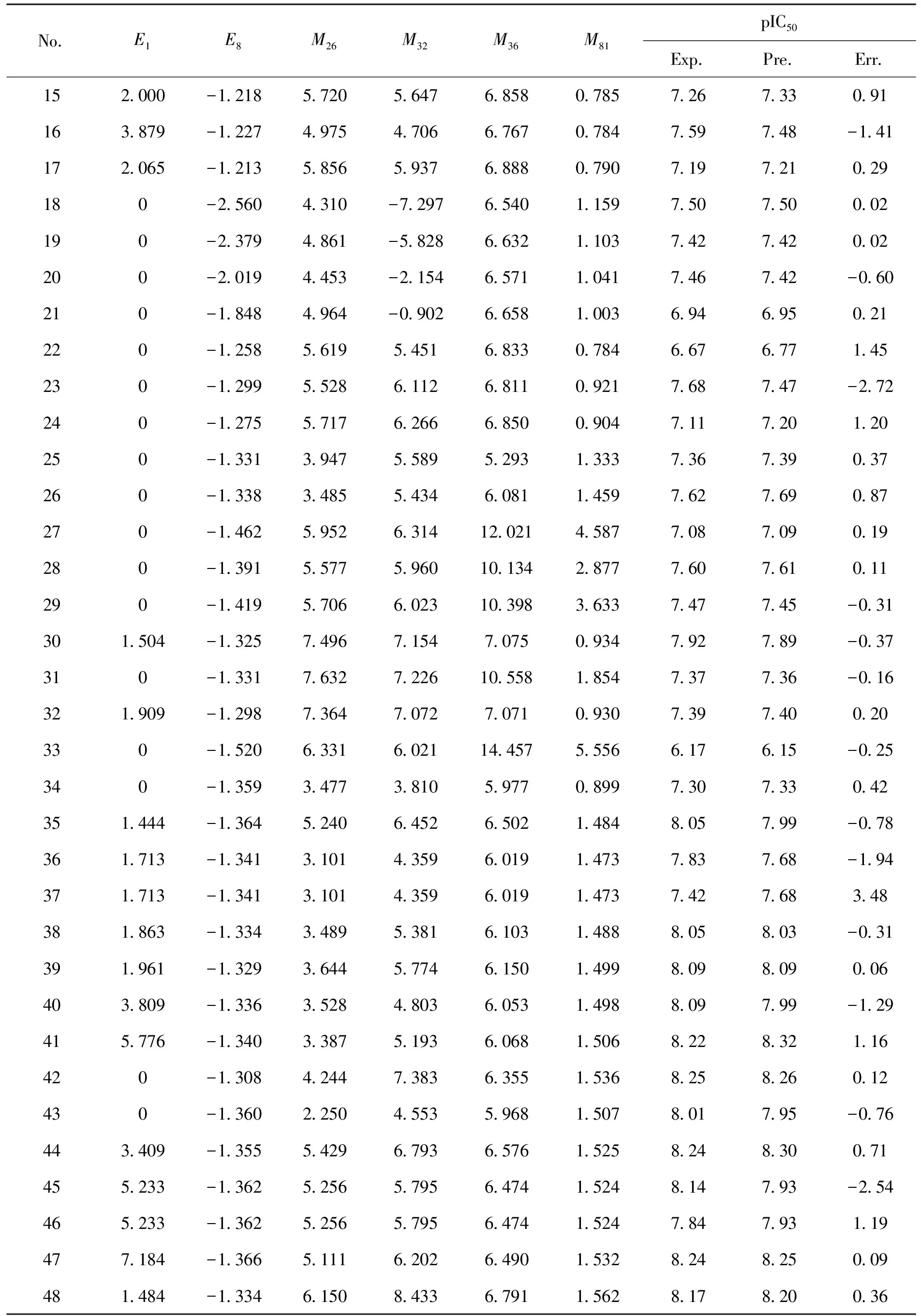
No.E1 E8 M26M32M36M81pIC50 Exp.Pre.Err.15 2.000-1.2185.7205.6476.8580.7857.267.330.91 16 3.879-1.2274.9754.7066.7670.7847.597.48-1.41 17 2.065-1.2135.8565.9376.8880.7907.197.210.29 18 0-2.5604.310-7.2976.5401.1597.507.500.02 19 0-2.3794.861-5.8286.6321.1037.427.420.02 20 0-2.0194.453-2.1546.5711.0417.467.42-0.60 21 0-1.8484.964-0.9026.6581.0036.946.950.21 22 0-1.2585.6195.4516.8330.7846.676.771.45 23 0-1.2995.5286.1126.8110.9217.687.47-2.72 24 0-1.2755.7176.2666.8500.9047.117.201.20 25 0-1.3313.9475.5895.2931.3337.367.390.37 26 0-1.3383.4855.4346.0811.4597.627.690.87 27 0-1.4625.9526.31412.0214.5877.087.090.19 28 0-1.3915.5775.96010.1342.8777.607.610.11 290-1.4195.7066.02310.3983.6337.477.45-0.31 301.504-1.3257.4967.1547.0750.9347.927.89-0.37 310-1.3317.6327.22610.5581.8547.377.36-0.16 321.909-1.2987.3647.0727.0710.9307.397.400.20 330-1.5206.3316.02114.4575.5566.176.15-0.25 340-1.3593.4773.8105.9770.8997.307.330.42 351.444-1.3645.2406.4526.5021.4848.057.99-0.78 361.713-1.3413.1014.3596.0191.4737.837.68-1.94 371.713-1.3413.1014.3596.0191.4737.427.683.48 381.863-1.3343.4895.3816.1031.4888.058.03-0.31 391.961-1.3293.6445.7746.1501.4998.098.090.06 403.809-1.3363.5284.8036.0531.4988.097.99-1.29 415.776-1.3403.3875.1936.0681.5068.228.321.16 420-1.3084.2447.3836.3551.5368.258.260.12 430-1.3602.2504.5535.9681.5078.017.95-0.76 443.409-1.3555.4296.7936.5761.5258.248.300.71 455.233-1.3625.2565.7956.4741.5248.147.93-2.54 465.233-1.3625.2565.7956.4741.5247.847.931.19 477.184-1.3665.1116.2026.4901.5328.248.250.09 481.484-1.3346.1508.4336.7911.5628.178.200.36

3 QSAR模型的建构

3.1 多元回归分析

将48种喹诺酮羧酸衍生物的抑制活性pIC50,与优化筛选得到的6种结构参数E1，E8，M26，M32，M36和M81进行线性回归分析,得到方程为

pIC50=0.141E1-4.832E8-0.487M26+0.482M32+0.361M36-0.890M81-0.582

(2)

利用式(2)对喹诺酮羧酸衍生物的活性值进行预测,所得预测值与实验值之间的相对平均误差为2.69%,可以看出,多元回归模型的预测误差稍大。

3.2 模型稳定性检验

为检验是否存在“离域”的异常数据,可使用形象直观的雷达图定性评价,对以上建立的预测喹诺酮羧酸衍生物活性的48个模型Jackknifed相关系数R作雷达图(见图2),以检验的R值0.925作为圆心,相隔0.005为间距,48个模型的Jackknifed相关系数R值全部落在0.925～0.960之间,波动性很小,只有剔除33号分子所得模型的相关系数为0.959稍大外,其他模型的R值基本在0.944左右,说明这里所建构的模型不存在“异常离域数据”。

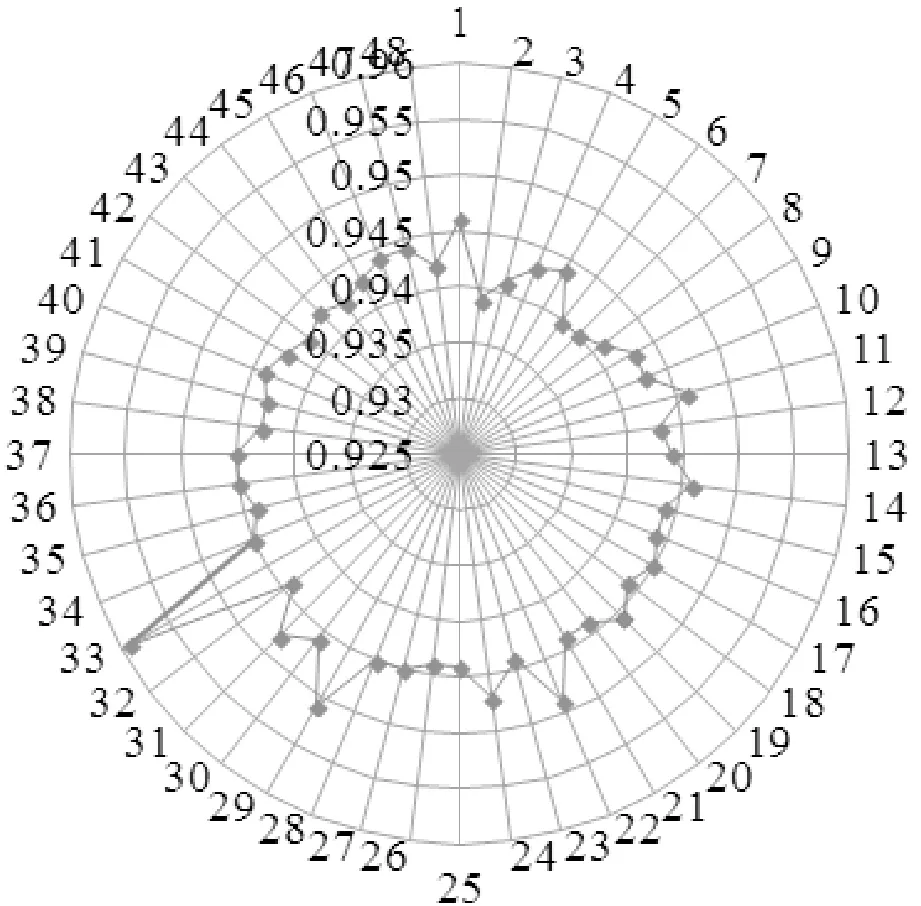
图2 Jackknifed相关系数R的雷达图Fig.2 Radar map of Jackknifed correlation coefficent R

用膨胀系数(VIF)来检验模型中各变量的相关程度,VIF定义为:VIF=1/(1-R2),这里的R为方程中某一个自变量与其他变量之间的相关系数,当VIF>10,则表示方程不稳定,这里计算得到的VIF 值分别为1，10，5，10，9，5,基本满足要求。

表4 Jackknifed R的检验Tab.4 Inspection of jackknifed R

3.3 神经网络模型

为提高预测喹诺酮羧酸类衍生物活性的预测精度,结合BP神经网络法更深入研究。将多元回归建模分析中筛选的E1，E8，M26，M32，M36和M81共6个参数作为神经网络的输入层神经元,将48种喹诺酮羧酸衍生物活性作为输出层节点,综合Andrea[25]及许禄等[26]学者对隐含层节点取值的建议规则可得

2.2>n/M≥1.4

(3)

式中：n为样本的分子个数,M为神经网络的总权重，M的取值为

M=(L+1)×Y+(Y+1)C

(4)

式(4)中，L，Y，C分别为神经网络中输入层节点、隐含层节点及输出层节点。这里6个结构参数作为输入层节点L=6; 喹诺酮羧酸衍生物活性作为输出层神经元C=1; 根据式(3)和式(4)计算得到隐含层节点Y可取3或4,经测试,当Y取4时,所得结果更优,因此网络结构采用6-4-1方式。将样本分为三个组别:第一组为训练集,选择每5个数据中的第1，3，5个数据;第二组为测试集,选择每5个数据中的第2个;第三组为验证集,选择每5个数据中的第4个。在Matlab环境运行中计算得到预测喹诺酮羧酸衍生物活性的神经网络模型的总相关系数为0.992 5,训练集、测试集和验证集的相关系数分别为R1=0.990 0，R2=0.995 8，R3=0.997 9,利用该模型预测的喹诺酮羧酸衍生物活性值与实验值较为吻合,平均相对误差只有0.87%,该误差比使用多元回归法模型的平均相对误差2.69%明显要小,将两种方法所得预测值与实验值作关系图(见图3和图4),可以看出,神经网络法的预测精度明显优于多元回归法。神经网络模型的权重和偏置见表5。

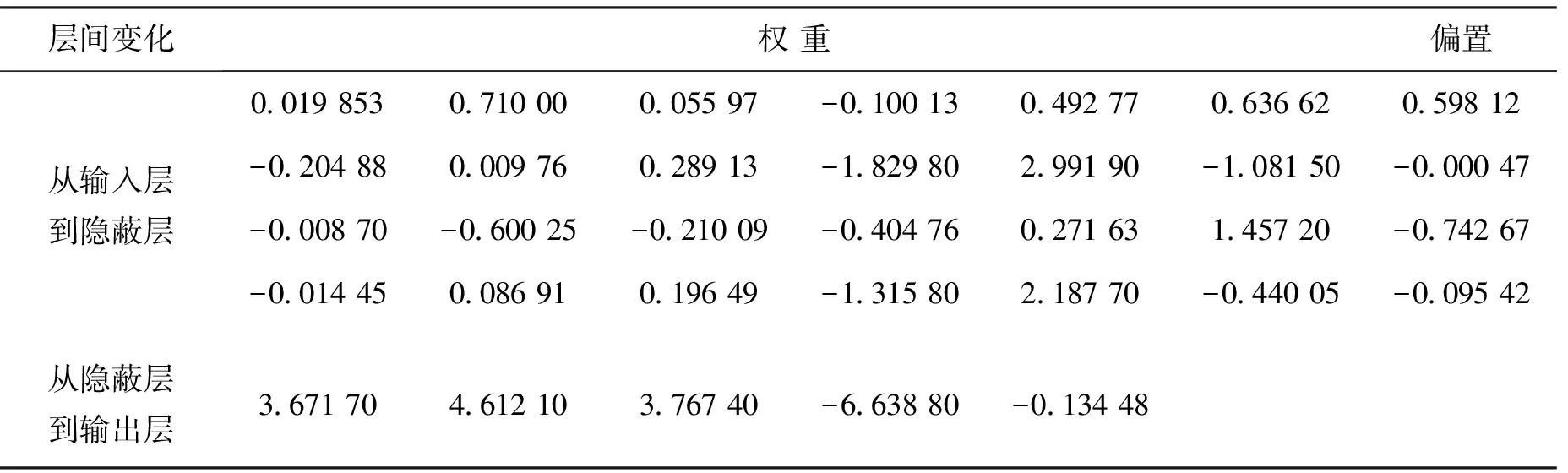
表5 神经网络模型的权重和偏置Tab.5 Weights and bias of neural network model

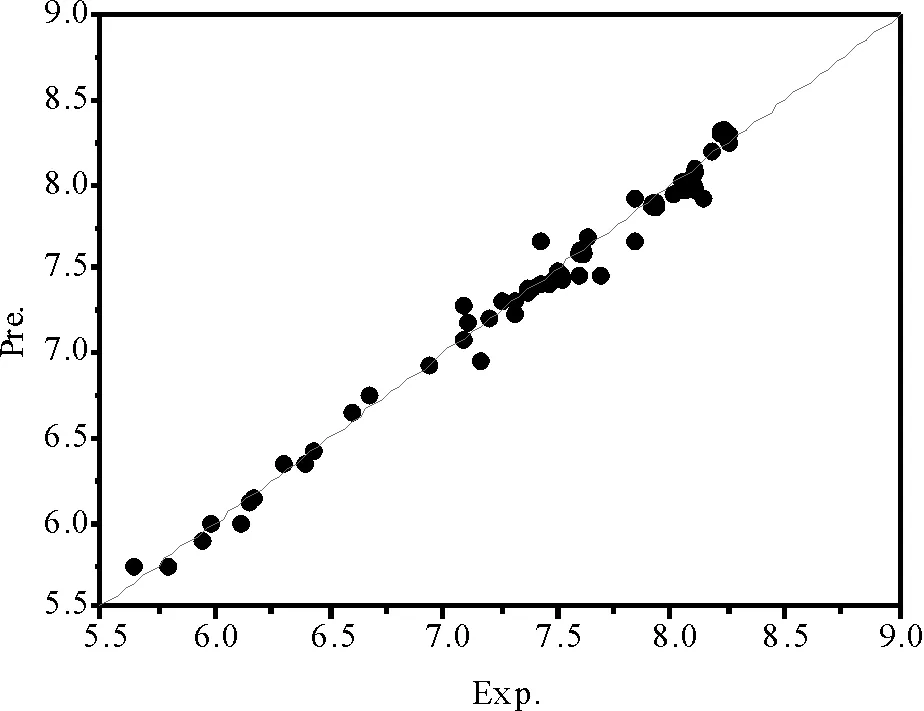
图3 神经网络法预测值和实验值关系图Fig.3 Relationship between prediction value and experimental value by neural network method

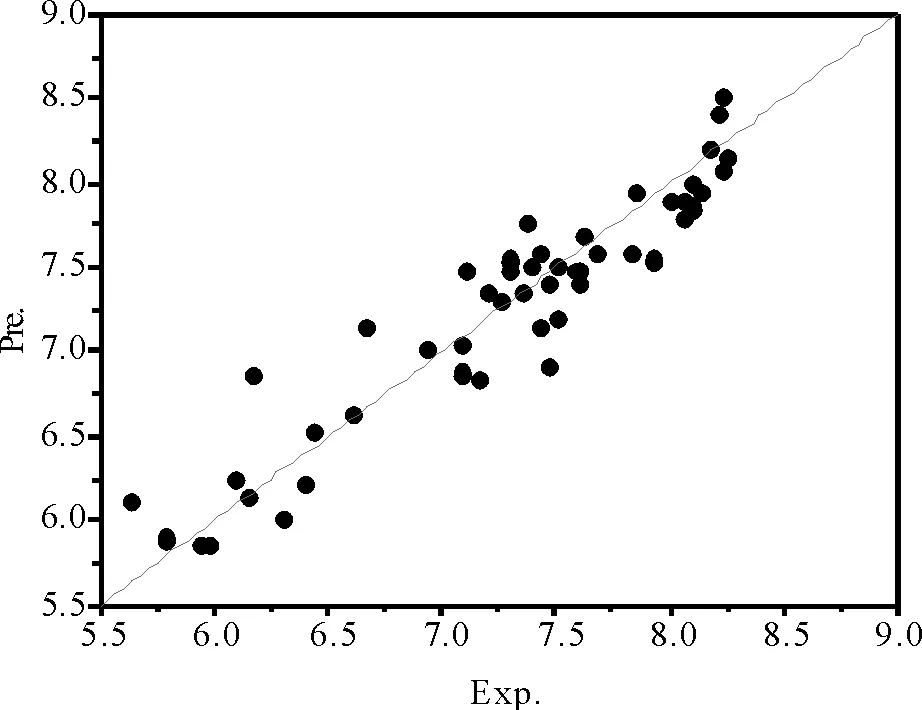
图4 多元回归法预测值和实验值关系图Fig.4 Relationship between prediction value and experimental value by multivariate regressive method

4 结果与讨论