浅析向量在数学解题过程中的应用

摘要：向量作为高中数学重要的知识点之一，其既可视为代数问题，又可视为几何问题，具有双重性，是高考中的常客，无论是选择题、填空题，还是解答题中均有體现，应引起学生们的高度重视。本文从向量的基本知识点入手，进一步分析其在数学解题过程中的应用。

关键词：向量   代数问题   几何问题

向量作为一种基本的解题工具，常被应用于其他常考知识点中，如不等式、数列等代数问题，平面几何、立体几何等几何问题。要想熟练运用这种工具，就必须牢固掌握其基本知识，做到活学活用。

一、向量的基本知识点

向量是兼具大小和方向的量，一般用     或  表示，其长度大小又称为向量的模，用     或   表示。当然，在高中向量知识中，最长常用的时候坐标表示                                。下面对向量中的常用知识进行了简要总结。

向量基本运算：设                                  ，那么

;                              ;                    。在加减、数乘运算上，基本没有变化，但对于向量的乘法就与之前所学的有很大不同。     称为向量的叉乘、外积，它不满足常用的交换律与结合律，具体表现为：                  ;                                而

;而      称为向量的点乘、内积，其计算公式为：

。因此，在进行向量的乘法计算时需格外注意，需区分是叉乘还是点乘。

向量平行定理（不考虑零向量）：向量  与向量  平行的充要条件为         且          。

向量垂直定理（不考虑零向量）：向量  与向量  垂直的充要条件为                               。

通过对向量基本知识点的简要分析，易知用向量的代数计算可以反应向量的几何关系，且还能进行角度的分析，这就可以用坐标表示向量，进而将其与几何关系联系起来，这种方法也是求解几何问题最常用方法之一，尤其体现在立体几何中。

二、向量在解题过程中的具体应用

高中数学习题主要可分为代数问题与几何问题两大类，在这两类问题中，均有向量的用武之地。下面就以具体的习题来阐述向量的基本知识在解题过程中的应用。

（一）代数问题

例题1：证明对任意实数a、b、c、d，均有

。

解析：这道题虽然字母较多，但证明起来并不难，正常展开即可。当然，由于题中既有平方和的形式，又有相互乘积之和的形式，与向量的模长与内积形式一致，因此，不妨设向量                          ，且   与  的夹角为θ，应有                     ，对两边同时取绝对值，有                          。因为             ，所以

，即                                     ，证明完毕。可将这一关系做进一步延伸，可推广到一般情形即

。

上述这一延伸结论可以作为不等式证明的一种技巧，比如，a、b、c∈R+，且                    ，求证                       。解析：构造向量                        ，                          ，根据上述延伸结论可知，

。

例题2：已知向量                             。

（i）求證       为等比数列;（ii）当                时，                 ，数列

的前n项和Sn。

解析：（i）                                                               ，所以     为等比数列;（ii）                                             ，因为是向量夹角，所以            ，故                          。

（二）几何问题

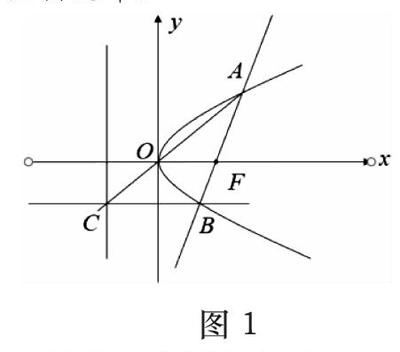
例题3：如图1所示，F是抛物线                         的焦点，一直线过点F与抛物线交于A、B两点，过B作x轴的平行线，交准线与点C，求证直线AC经过原点。

解析：设                                                            ，则

。要证直线AC经过原点，只需证                     ，即                                     。因为直线AB经过点F，所以                       ，即

，

证明完毕。

图1

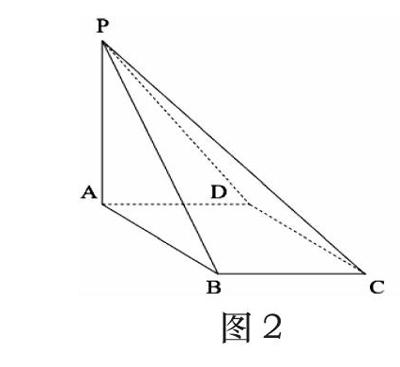
例题4：在四棱锥P-ABCD中，PA平面ABCD，且ABCD是边长为2的菱形，BAD60。（i）求证BD平面PAC;（ii）若PAAB，求PB与AC所成角的余弦值？

解析：（i）根据题中描述，绘制四棱锥P-ABCD如图2所示，方便寻找关系。因为PA平面ABCD，所以PABD，又因为ABCD是菱形，所以BDAC，进而证明出BD平面PAC;（ii）在这种立体几何求成角问题中，最常用的方法就是在给定的几何体上建立合理的坐标系，用向量的方式表示这两条直线，进而求出夹角的余弦值。本题中，以A为原点、AP为z轴，AD为x轴建立空间直角坐标系，如图3所示。根据题中的数量关系，易得出所需个点坐标A                                                               ，所以 ，                 ，故   。

图2                                图3

三、结语

总之，向量因其自身代数与几何的双重性，使之在高中数学的解题过程中具有极大的实用性，也是数形结合思想的一种体现，尤其是在立体几何求线线夹角、线面夹角、二面角问题中应用的极为广泛，是高考中的常客，学生们应对予以重视，充分理解向量的基本知识点，对向量的具体应用类型进行归纳总结，以拓宽学生的解题思路，提升综合应用能力。

参考文献：

[1]王军玲.向量在高中数学解题中的应用[D].西北大学，2017.

[2]陈纪源.向量在高中数学解题中的应用研究[J].数学学习与研究，2018，（03）：64.

[3]麦康玲.数学分析思想在高中数学解题中的应用[J].科学文汇（下旬刊），2015，（05）：110-111.

（作者简介：黄亦凡，高中学历，南昌市第二中学，研究方向：数学方向。）