南通地区冻结黏土蠕变特性试验研究★
束 阁 张 雪 陈雨嘉 王天祺
(1.南通职业大学建筑工程学院,江苏 南通 226001; 2.南通大学土木与交通工程学院,江苏 南通 226001)
0 引言
随着我国沿海开放城市交通大发展,南通城市轨道交通地铁一号线二号线的建设正在紧张有序的开展。在地铁施工过程中,冻结法建井成为关键技术得到重视[1]。大量冻结法工程实际显示,地铁施工中典型土层的冻土蠕变力学特性将对地铁施工起到较为关键的影响作用[2-5]。
1 土样采集及试验方法
1.1 土样采集
在地铁施工段开挖过程中取得典型土层粘土芯样。实验室土样试件的制作严格参照国家标准,形状采用圆柱体,大小为φ50 mm×100 mm(误差1.0%)。
1.2 试验装置及方法
1)试验装置。冻土单轴试验在WDT-100试验机上进行,其试验数据采集全由计算机控制系统自动完成,试验装置加载极限为100 kN,精度1%,冻结温度可达-50 ℃。
2)抗压试验方法。抗压试验在负温条件下分别进行三组。选取南通典型土层的粘土试件3个,常温养护后,在-5 ℃,-10 ℃和-15 ℃三种温度等级下进行单轴无侧限抗压强度试验[6]。
3)蠕变试验方法。安装并连接好相关设备及仪器。蠕变试验荷载应力水平分别取0.3倍,0.5倍和0.7倍上述抗压强度,试验温度同前。按此方法进行多次试验,等到冻土试件变形趋于稳定或趋于某个极小常数时,记录下最终蠕变值,试验结束[7]。
2 单轴抗压试验
2.1 单轴抗压试验结果
分别在-5 ℃,-10 ℃和-15 ℃三种不同温度下,根据试验规范按要求对典型土层的冻结黏土试件进行无侧限单轴抗压试验,每组试验选取3个不同试件,其结果如表1所示。

表1 典型土层的抗压试验
2.2 单轴应力应变关系曲线
根据试验结果,以第2组数据为例,画出单轴应力应变的关系曲线,如图1所示。

3 单轴蠕变试验
3.1 单轴蠕变试验结果
冻土的蠕变性能是反映冻结特性的主要指标,常用蠕变模型来表征[8]。传统的冻土蠕变模型可表示为式(1):
ε=AσBtC
(1)
其中,A为蠕变常数;B为应力常数;C为时间常数;σ为蠕变应力;t为蠕变时间;ε为蠕变发生时候产生的应变值。

表2 第1组冻土蠕变结果
对南通地铁典型土层冻结黏土(10 m~20 m为第1组,20 m~40 m为第2组)进行3种不同温度水平下的蠕变试验,每种温度下3个试件,蠕变试验结果如表2,表3所示。

表3 第2组冻土蠕变结果
3.2 蠕变曲线
第二组数据为例,根据表1应力等级画出蠕变关系曲线,如图2所示。
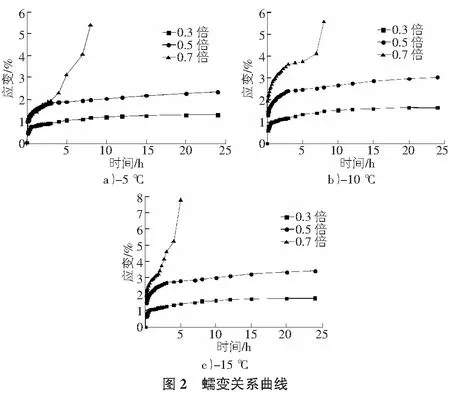
4 蠕变模型的拟合优化
从以上两组冻土的试验结果发现:在应力水平较低(0.3倍)和中等(0.5倍)时候,冻土蠕变最终趋于稳定,而应力水平较高时(0.7倍),蠕变趋于不稳定[9]。为此,不失一般性,需要对冻结蠕变回归公式进行拟合优化,才能更好的表征实际工程冻土的蠕变特性。
因此,蠕变模型表达式可改写成模糊表达式,如式(2)所示:
(2)


(3)
(4)
(5)
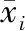
结合上述模糊分析结果,分别在不同温度水平下利用MATLAB工具数值拟合式(2)中的其他参数,最终可获得南通地铁典型土层冻结黏土在-5 ℃,-10 ℃和-15 ℃下的蠕变优化模型[10],具体如式(6)~式(8)所示:
1)在-5 ℃情况下应变(%)与时间(h)关系:
ε=1.350σ1.253t0.118
(6)
2)在-10 ℃情况下应变(%)与时间(h)关系:
ε=0.982σ1.018t0.148
(7)
3)在-15 ℃情况下应变(%)与时间(h)关系:
ε=0.789σ1.099t0.075
(8)
为验证优化后式(6)~式(8)的合理性,故另取不同施工段黏土,进行上述蠕变试验比较其公式计算值与试验值,见表4。
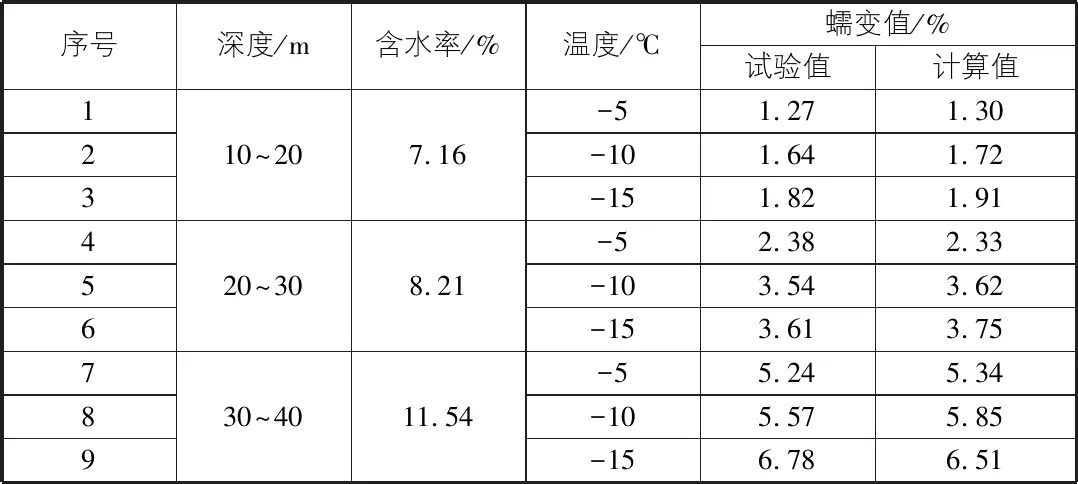
表4 蠕变计算值与试验值对比
根据蠕变试验值与优化公式计算值结果对比,发现优化后的蠕变公式在不同温度情况下均能和试验数据拟合较好,其误差水平均控制在2%~5%之间。由此说明文中公式能很好的反映南通地区典型土层冻土蠕变的各阶段特性,具有工程参考性。
5 结论
1)通过对南通典型土层冻土单轴蠕变试验发现:在应力水平较低(0.3倍)和中等(0.5倍)时候,冻土蠕变最终趋于稳定,而应力水平较高时(0.7倍),蠕变趋于不稳定。为此,不失一般性,需要对冻结蠕变回归公式进行拟合优化,才能更好的表征实际工程冻土的蠕变特性。
2)结合工程的复杂多变,对传统蠕变公式进行模糊优化,发现优化后的蠕变公式在不同温度情况下均能和试验数据拟合较好,其误差水平均控制在2%~5%之间。说明文中公式能很好的反映南通地区典型土层冻土蠕变的各阶段特性,具有工程参考性。

