Modeling of the whole process of shock wave overpressure of freefield air explosion

Zai-qing Xue, Shunping Li, Chun-liang Xin, Li-ping Shi, Hong-bin Wu

Beijing Institute of Space Long March Vehicle, Beijing,100076, China

Keywords:Air explosion Shock wave overpressure Free field Experimental verification Numerical simulation

ABSTRACT The waveform of the explosion shock wave under free-field air explosion is an extremely complex problem. It is generally considered that the waveform consists of overpressure peak, positive pressure zone and negative pressure zone. Most of current practice usually considers only the positive pressure.Many empirical relations are available to predict overpressure peak,the positive pressure action time and pressure decay law. However, there are few models that can predict the whole waveform. The whole process of explosion shock wave overpressure, which was expressed as the product of the three factor functions of peak, attenuation and oscillation, was proposed in the present work. According to the principle of explosion similarity, the scaled parameters were introduced and the empirical formula was absorbed to form a mathematical model of shock wave overpressure. Parametric numerical simulations of free-field air explosions were conducted. By experimental verification of the AUTODYN numerical method and comparing the analytical and simulated curves, the model is proved to be accurate to calculate the shock wave overpressure under free-field air explosion.In addition,through the model the shock wave overpressure at different time and distance can be displayed in three dimensions.The model makes the time needed for theoretical calculation much less than that for numerical simulation.

1. Introduction

The waveform structure of the air explosion shock wave is generally considered to consist of overpressure peak, positive pressure zone and negative pressure zone, as shown in Fig. 1, in which, the overpressure peak is the most concerned, followed by the positive pressure action time and pressure decay law.As for the negative pressure zone and the subsequent oscillation zone, there is few research information published.

Many scholars have carried out research on the overpressure and propagation laws of explosive shock waves,and summarized a number of overpressure experience and semi-empirical formulas[1‒5].The formulas often used to calculate overpressure are Henrch formula[1],Brode formula[2]and Friedlander formula[3].In 1984,based on a large number of experimental data, Kingery [4,6and7]put forward the Kingery-Bulmash model to calculate overpressure, which has been widely used. After a series of tests, the Kingery-Bulmash model was modified by Kingery in 1998 [8,9]which makes the far-field overpressure prediction much higher than before.

All these formulas assume that positive pressure decays exponentially,and do not consider the role of negative pressure zone.In the far-field of air explosion shock wave, the structural response might be influenced by both the positive and negative phases of the pressure pulse, and their interaction with the structure [10].Regarding the negative pressure zone, Martin Larcher [11]uses a double-fold line to approximate the pressure in the negative pressure zone, and the negative pressure peak value is given as:

where w is the TNT equivalent of the charge and the unit is kg,R is the distance from detonation and the unit is m, and pmis overpressure and the unit is MPa.When the overpressure peak is lower than -0.01 MPa,it is limited to -0.01 MPa.Because it is too simple that the double-fold line model divides the duration of the negative pressure area equally,there will be a big deviation from the actual situation.

Fig.1. Typical waveform structure of the air explosion shock wave.

At present there is no model that can predict the whole process of shock wave overpressure under free-field air explosion. And in the research of damage and protection, in order to obtain the mechanical response of the target or equipment under impact, it is necessary to input accurate time-space distribution data of the shock wave,including the negative pressure region waveform and even the subsequent oscillation data.Therefore,the research on the shock wave modeling of the whole process is very important.In the present work,a formula,which was expressed as the product of the three factor functions of peak, attenuation and oscillation, was established to predict the shock wave overpressure of free-field air explosion. In this formula, the scaled parameters were absorbed and well fitted by numerical data. The results obtained from the formula are consistent with the data of numerical simulation models,which indicates that the formula can accurately predict the shock wave overpressure of free-field air explosion at different times and distances.The new formula can be used to calculate the shock wave overpressure of free-field air explosion, including overpressure peak, the positive pressure action time and pressure decay law, and the negative pressure zone and the subsequent oscillation zone.

2. Modeling

At a certain point in the free field of air explosion, the shock waveform is generally combined by the attenuation of the overpressure peak and the periodic oscillation of the gas medium,which can be expressed by the following formula,

where pmis the overpressure peak,the function f(tg1)describes the attenuation of the overpressure with time, and the function g(tg2)describes the periodic oscillation of the pressure with time.tg1and tg2are two scaled-time.The formation and propagation of explosive shock waves in the air conform to the law of explosion similarity.In order to make Equation(2)applicable to different explosive charges,scaled-parameters are needed to describe the distance and time.The scaled-distance is defined as

where R is the distance from the detonation point, w is the TNT equivalent of the explosive. As w increases or R changes, the duration and attenuation of the shock wave will change accordingly. In order to comply with the law of explosion similarity, the sum of the indices of R and ffiffiffiw3p in the scaled-time definition must be 1. So the scaled-time should be defined as

where n is a constant, and t is time. When different n values are taken, different kinds of scaled-time definitions are formed.

In practical applications,the overpressure peak of Equation(2)is usually expressed in the following form,

where Rgis the scaled-distance between the point and the detonation point. s1, s2, and s3are constants.

The function f ðtg1Þ in Equation (2) describes the attenuation of pressure with time.The form of the negative exponential function is taken here,

where a, b, and k are constants. The units of a and tg1should be correspond to each other and are reciprocal to each other. tg1is a scaled-time formed by Equation (4) with different value of n.

The function g(tg2) in Equation (2) describes the periodic oscillation of pressure with time, which is expressed in the form of a cosine function.

where c and q are constants,the unit of c should correspond to tg2.tg2is another scaled-time formed by Equation (4) with difference value of n.The denominator cosq is only for satisfying the result of 1 when tg2is 0.

Substituting Equation (6) and Equation (7) into Equation (2),

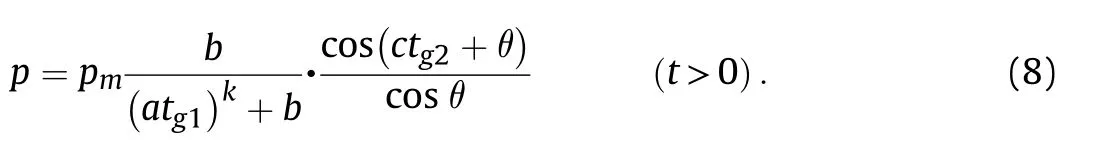
3. Parameter determination of the model

With the development of numerical method, many explosion problems has been solved by numerical simulation [12‒14]. Explosion shock wave can be solved more accurately [11,15‒17].Generally speaking, the software based on finite difference and finite volume method,such as AUTODYN,Air3D,DYTRAN,DYSMAS and so on, is more accurate than finite element software, such as LS-DYNA and EUROPLEXUS.The AUTODYN numerical results of the free-field explosion are used to determine the parameters of the shock wave model.

In order to simulate the spherical symmetry explosion, a twodimensional axisymmetric wedge model in Autodyn2D [18] is used to establish a small hollow wedge-shaped charge with an inner radius of 2 mm and an outer radius of 106 mm.The corresponding spherical TNT charge is 8 kg.The same modeling method is used for air domain, which has an inner radius on the outer surface of the charge and an outer radius of 20 m. The established numerical model is shown in Fig. 2. The grid number of explosion and air domain is 52 and 9949 respectively.The interval of the grid is 2 mm.

Fig. 2. Numerical model of free-field explosion.

Air and TNT are simulated by Euler processor.Air mass density is 1.225 kg m-3, air initial internal energy is 2.068×105kJ kg-1, and ideal gas constant is 1.4, which are standard constants of air and TNT from Autodyn2D material library.And air is presumed to have equation of state of ideal gas. The TNT charge detonation product adopts the JWL equation of state, that is, the pressure of the detonation product is

where E is the unit mass internal energy,V is the specific volume.A,B,R1,R2,and u are constants.The first term on the right end of the equation plays a major role in the high pressure section.The second term plays a major role in the medium pressure section. And the third term represents the low pressure section.In the later stage of the expansion of the detonation product,the effects of the first and second term in the equation are negligible.In order to speed up the solution,the explosive equation of state is converted from the JWL equation of state to a simpler ideal gas state equation. The JWL equation of state for explosive detonation products is taken from the AUTODYN material database, seeing Table 1. Where r0Tis the initial density of TNT charge, D is the detonation velocity, E0is the initial internal energy, and PCJis the detonation pressure.

3.1. Parameter determination of pm

According to experimental data of TNT shock wave overpressure under free-field air explosion,the following similarity ratio formula was proposed by Henrch [1],

By numerical simulation,a formula of shock wave overpressure of infinite ideal gas was fitted by Brode as follows [2],where the unit of pmis MPa, and the unit of scaled-distance Rgis

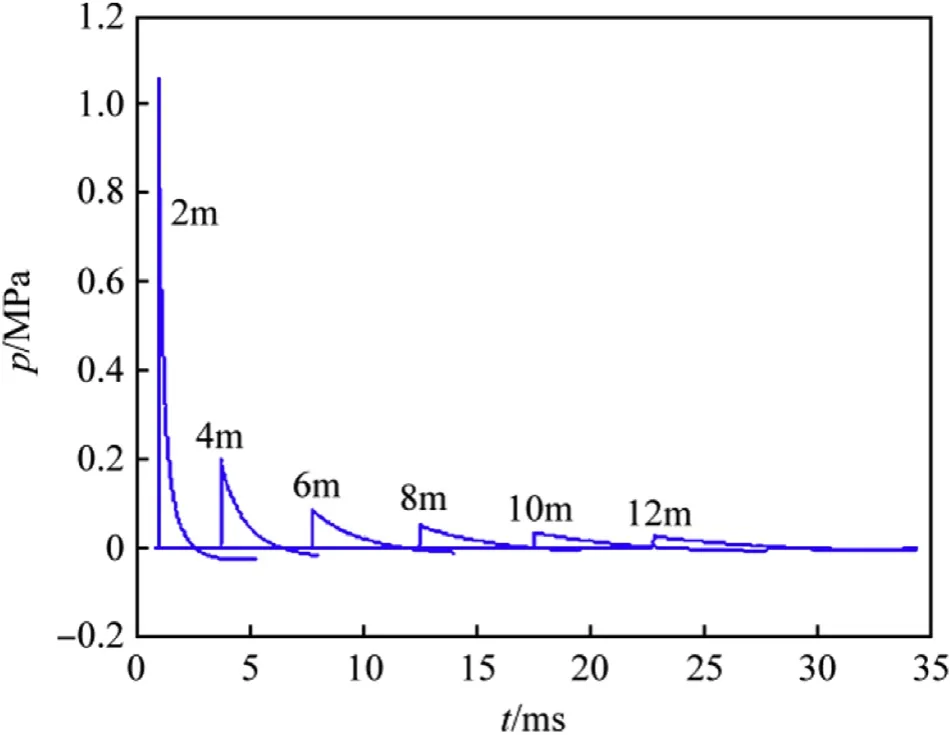
Fig. 3. Numerical overpressure at different positions from the detonation point.

According to Ruce Wang[19],the overpressure peak of spherical charge explosion can be calculated by the following formula,where the unit of pmis MPa, and the unit of RgisThe comparison shows that the formula is very close to the simulation result of AUTODYN when Rgis larger than 0.5. And no change is needed.The values of s1,s2,and s3in equation(12)should be 0.082,0.26 and 0.69 respectively. The formula is no longer applicable when Rgis smaller than 0.5.

3.2. Parameter determination of g(tg2)

The parameter values of g(tg2) and f(tg1) require reliable data support. When the accurate and credible experimental data is insufficient,the rigorous numerical results are a good basis.In this paper, Fig. 2, the pressure waveform calculated by AUTODYN, is used to determine the parameters. The action time of the positive and the negative pressure zone of the shock wave is determined by the factor function g(tg2), and there are clear numerical results. So parameters of g(tg2) is determined firstly. Parameters of f(tg1) are further determined based on the parameters.

In the function g(tg2),the relationship between the positive and negative pressure action time and the distance is determined by tg2.According to the comparative analysis and fitting of the curve data on the values at different distances,the value of n in Equation(4)is determined to be 0.75. At this time

In the function g(tg2), the oscillation period of the pressure is determined by c, that is, the boundary point between the positive pressure zone and the negative pressure zone is determined. The distribution of the action time of the positive and negative pressure zones is determined by q. When q is p/4, the positive pressureaction time is 1/4 of the negative pressure action time.Based on the extrapolation analysis of the numerical curve shown in Fig.4,q¼p/4 is considered to be suitable.Similarly,according to the oscillation period calculated from numerical results, the value of c is 0.9575 when the time unit is ms,the distance unit is m,the mass unit is kg,and the pressure unit is MPa.Then

Table 1 JWL equation of state parameters of TNT detonation product.

Fig. 4. Extrapolation analysis of numerical data with scaled-distance of 1.

3.2.1. Parameter determination of f(tg1)

In the function f(tg1), tg1is closely related to the shape of the shock wave attenuation curve changing with the distance. According to the comparative analysis of the numerical curve at different distances, it is considered that a value of 1.75 for n in Equation(4)is suitable when the time unit is ms,the distance unit is m, and the mass unit is kg. Then

In the function f(tg1),the variation law of the pressure waveform at different times and different distances is determined by a and k.According to the analysis of the numerical curve Fig.2,the values of a and k are 1.915 and 1.4 respectively when the time unit is ms,the distance unit is m,the mass unit is kg,and the pressure unit is MPa.The value is of b is mainly used to ensure that the value of f(tg1)is 1 when tg1is 0.And its value has a certain influence on the waveform.This paper takes 0.13 as b. So there is

So far,all the parameters in the free-field explosion shock wave model have been determined. Substituting Equations (13)e(16)into Equation (2),

Substituting Equation (3) into Equation (12),

Substituting equation (18) into Equation (17),

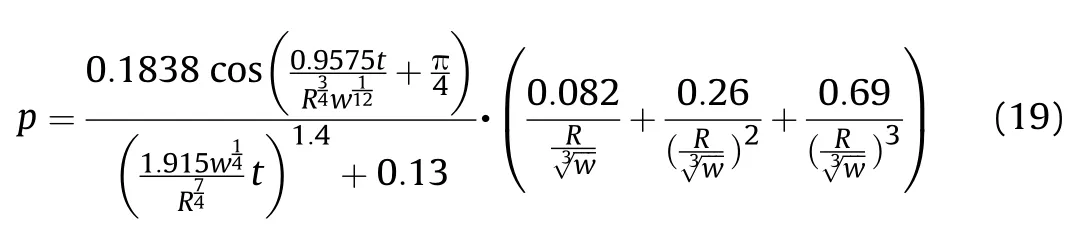
where t≥0. P is 0 when t＜0.

This formula(19) is the model of the free-field pressure of the explosion shock wave.It should be noted that the model is valid in the range of the scaled-distance bigger than 0.5.

4. Verification

4.1. Experimental verification of the numerical method

In order to confirm the accuracy of AUTODYN numerical method,a near-surface explosion experiment is implemented.The near-surface explosion shock wave will experience more complicated conditions than free-field explosions, such as free-field propagation, ground positive reflection, ground oblique reflection and Mach reflection,which make the verification of the numerical method more rigorous.

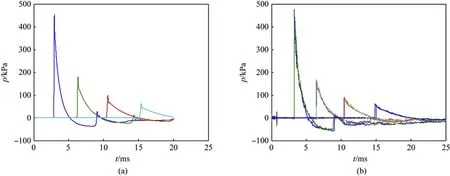
A two-dimensional axisymmetric model of AUTODYN is used to establish a cylinder-shaped TNT with a charge of 5 kg.The height from the ground is 1.5 m.The air domain has a radius of 20 m and a height of 7.5 m. The established numerical model is shown in Fig. 5(a). The numerical shock wave propagation and the groundgenerated Mach reflection process are shown in Fig. 5(b) and (c).The result of overpressure curve is shown in Fig.7(a).

The experiment of 5 kg cylindrical TNT near ground explosion was carried out. The experimental setup is shown in Fig. 6. The height of the TNT charge from the ground is 1.5 m.Two sensors are placed at 3 m, 5 m, 7 m and 9 m from the charge respectively. The pressure sensor is used to test the horizontal shock wave overpressure curve. The measured ground reflection overpressure curves are shown in Fig. 7(b).

From Figs.7(a)and Fig.6(b),the peak value and propagation of the shock wave calculated by AUTODYN are in good agreement with the experimental results.The simulation data is considered to be credible.

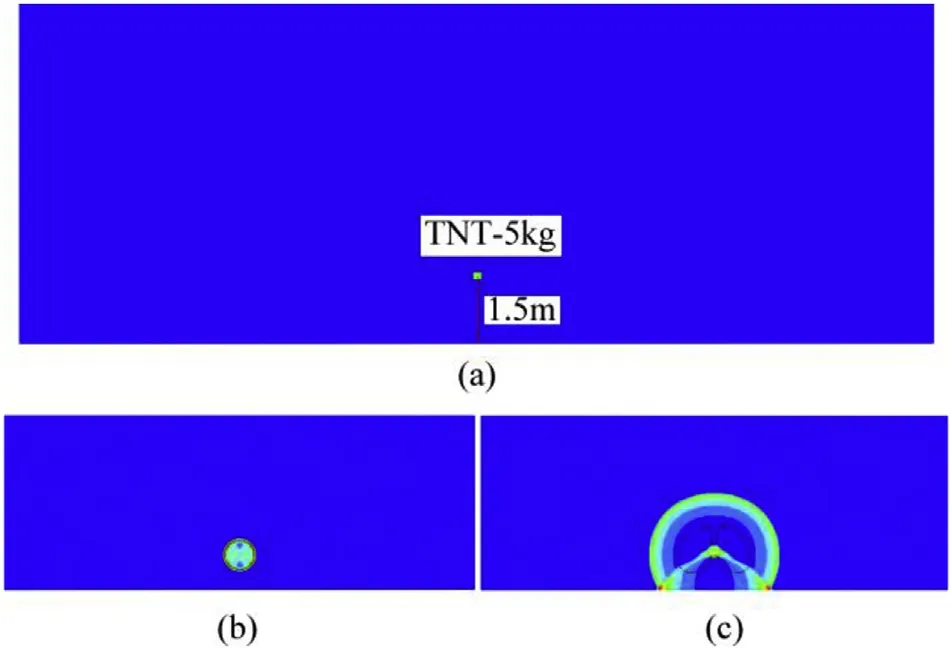
Fig. 5. Numerical model of free-field explosion.

Fig. 6. Experiment setup diagram.

4.2. Numerical verification

From the detonation moment,defining the scaled-time tdgwhen the front edge of the shock wave reaches a certain position is

where tdis the time when the front edge of the shock wave reaches a certain position,and the unit is ms.

According to the relationship between the position of the shock wave front and the time calculated by the numerical value, the scaled-distance of the shock wave reaching at a certain scaled-time can be fitted,and when tdg≥0.1,

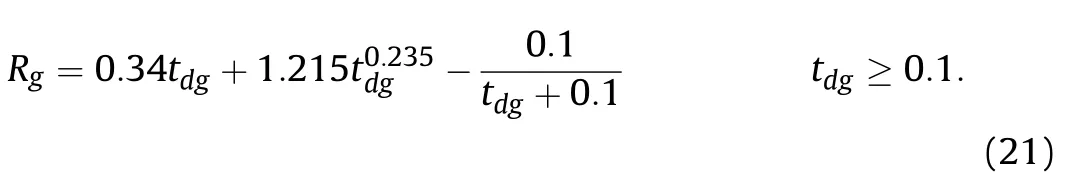
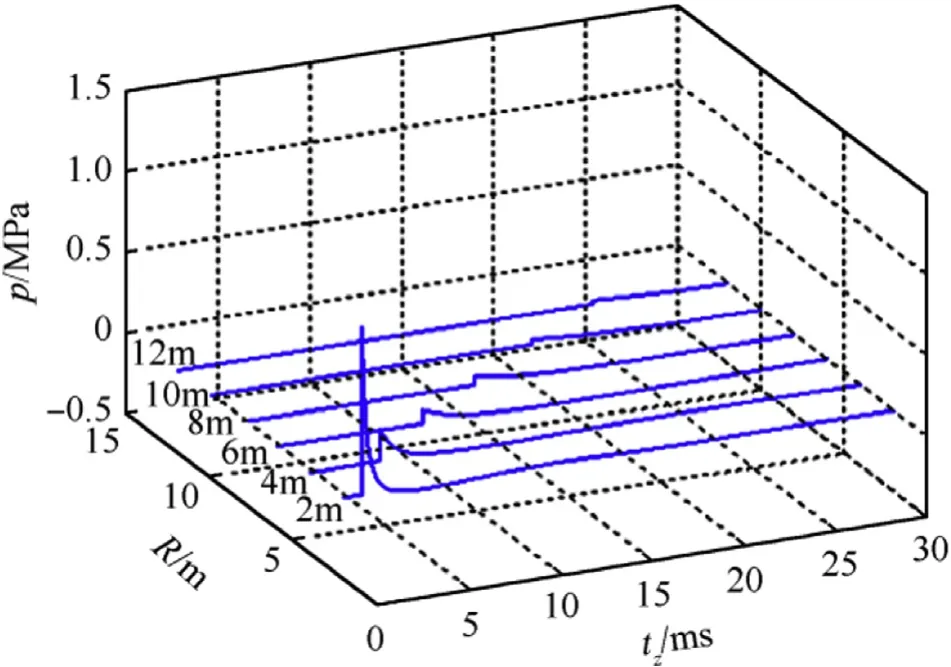
where tdgis the scaled-time.When 0

Substituting Equations (3) and (18) into equation (19)

Let the total time from the detonation time be tz, then the relationship between the time t in Equation(17)and the total time in Equation (20) is The equations, consisting of Equations (17), (20) and (21) can completely predict the spatiotemporal characteristics of the freefield overpressure of the explosion shock wave. In order to visually display the accuracy of the model,the results of the calculation can be compared with the results of the numerical method. Fig. 8 shows the pressure curves of shock waves at different distances of 64 kg spherical TNT charge of analytical and simulated methods,respectively. Fig. 9 shows the analytical and simulated curves of 1 kg spherical TNT charge. As can be seen from the curves in the figures, the two curves are in very good agreement, respectively.

Fig.9. Comparison of shock wave pressure-time curves of 1 kg TNT charge at multiple distances of analytical and simulated calculations.

Fig. 7. Numerical(a) and experimental(b) overpressure curve.

Fig.10. Shock wave overpressure-distance curves at multiple times.

Fig.11. Shock wave overpressure-time curves at multiple distances.

In addition, equations (17), (20) and (21) can describe the relationship of shock wave pressure and distance at different times,and the relationship of shock wave pressure and time at different distances,which are shown as Fig.10 and Fig.11 respectively.Both the explosion is 8 kg spherical TNT charge.The shock wave pressure at different times and at different distances can be displayed and studied in three dimensions.

5. Conclusion

A new model establishment method of shock wave overpressure under free-field air explosion was studied in this paper.The free-field explosion shock wave overpressure was expressed as a product of the three factor functions of peak, attenuation and oscillation. The attenuation of the explosion shock wave conforms to the law of negative exponential decay,and the initial stage of the oscillation process basically conforms to the law of cosine oscillation.Further,the parameters of a,b,k,c and q were well fitted by the numerical data.By comparing the calculated results from Equations(17), (20) and (21) with numerical data, it was found that the analytical and simulated curves are in very good agreement,which indicates that the equations can accurately calculate the shock wave overpressure under free-field air explosion.Furthermore,the equations can realize three-dimensional display of the shock wave pressure with time and distance.

The new formulas of this model can predict shock wave pressure well of the free-field air explosion. But because that careful parameter determination is through simulation, and the ground reflection of explosion shock wave is so complex that the measurement of free-field overpressure in experiment is very difficult,new measurement methods should be developed and a wide range of test conditions should be carried out to modify the parameters in the formulas.Focusing on these issues,further investigation will be conducted in our succedent research based on the analytical model.

Acknowledgments

This work was partially sponsored by Foundation of PLA Rocket Force.