基于MRSVD与灰色理论的供输弹系统故障诊断研究

张航 潘宏侠 许昕 赵雄鹏

摘要：针对采集的供输弹系统测试信号成分复杂、故障难以识别问题，提出一种基于多分辨奇异值分解（MRSVD）与灰色理论的供输弹故障诊断方法。首先使用双树复小波的信号降噪方法进行信号预处理，使用MRSVD方法提取微弱故障特征，在不同层面将信号的特征信息表征出来;然后提取各分量的能量，归一化后作为特征值;最后将灰色理论引入到供输弹系统故障诊断中，经过灰色关联度分析，进行故障诊断。实验结果表明：该方法诊断结果准确率达86.7%，可有效进行故障识别。

关键词：供输弹系统;多分辨奇异值分解;灰色理论;故障诊断

中图分类号：TJ303.3 文献标志码：A 文章编号：1674-5124（2019）07-0147-05

收稿日期：2018-11-05;收到修改稿日期：2018-12-10

基金项目：国家自然科学基金资助项目（51675491）

作者简介：张航（1994-），男，陕西西安市人，硕士研究生，专业方向为复杂机电系统监测与故障诊断。

0 引言

火炮是现代炮兵的关键组成要素，作为大口径火炮重要组成部分，供输弹复杂系统具有使用频率高、不便于维修保养等特点，发生故障的概率较高[1]。供输弹系统处在恶劣的工作环境中，许多早期微弱故障难以及时发现排除，因此对供输弹系统做出有效的智能化故障预示和诊断具有重要意义[2]。

奇异值分解（singular value decomposition，SVD）算法具有良好的稳定性和不变性，被广泛应用于信号处理、故障诊断等领域[3]。多分辨奇异值分解（MRSVD）是基于SVD的一种信号分解方法，它可以提取信号中的微弱特征信息，同时还能对信号进行有效分解[4]。灰色理论作为研究小样本数据之间不确定关系问题的建模方法[5]，主要研究对象是“信息量少、样本空间小”的不确定性系统，通过对行为序列中的测试数据和已知标准模式数据之间的关联度分析，从而实现对数据序列描述和认识[6]。

对于供输弹系统的故障识别，许海伦[7]使用电流信号分析和支持向量机方法进行研究，但电流分析法对信号的微弱故障特征提取不完全，会丢失部分信息，并且支持向量机在求解问题分类时较为困难，计算难度大，故障难以识别。本文提出使用MRSVD与灰色理论方法，MRSVD可从强噪声背景下检测突变信息，信噪比高，可准确提取早期微弱故障特征;灰色理论所需样本少，计算量小，并且能达到较高精度，可作为长期预测方法。

1 MRSVD

MRSVD是在SVl]的基础上，加入矩阵二分递推结构的思想，利用二分递推原理构造相空间矩阵，对原始信号进行分解，可以得到一系列SVD的细节信号和近似信号[8]，对近似信号再进行下一层SVD处理，并且对每一层信号都取行数为2的构造矩阵，以此递推，可以获得不同分辨率的细节信号和近似信号，实现将复杂信号分解到不同层次子空间的分解，如图1所示。使用MRSVD方法对信号进行分解，最后对提取信号进行逆运算重构，即可实现对原始信号的降噪及特征提取[9]。

从图中可以看到，首先对于信号X=[x₁，x₂，…，x_n]构造二维Hankel矩阵：

然后对矩阵H进行SVD处理，得到：

H=A₁+D₁=λ₁₁u₁₁v₁₁^T+λ₁₂u₁₂v₁₂（2）其中，A₁为第一层近似信号，D₁为第一层细节信号。

根据图1 MRSVD过程可得第j次分解结果：

H_j=A_j+D_j=λ_j1u_j1v_j1^T+λ_j2u_j2v_j2^T（3）

这样，经过多层分解，就能将原始信号的细节特征和主体以多种层次的形式展现出来。

由于该理论的相空间矩阵构造简单，解决了SVD中确定相空间矩阵形式和维数的难题，以及对大数据分解计算量大、速度慢的缺点。同时，这种对信号分解的模式类似于小波分解，却克服了小波基的选择难和小波分解中的相漂问题[10]。

2 灰色理论

灰色关联分析研究不同事物和数据之间的关系，尤其体现在事物和数据之间微弱的差异，从而确定事物之间的相互关系和影响[11]。

灰色关联分析的实质是确定主行为序列和比较行为序列，与主行为序列做比较的子行为序列称为比较序列。对行为序列进行计算，并比较其相近程度，最终通过行为序列之间关联度的大小体现差异。该方法的一般流程为：1）确定主行为序列与比较序列;2）通过不同方法对关联度进行计算;3）依据关联度的大小，进行不同序列之间的比较[12]。

1）主行为序列和比较序列

假设主行为序列和比较序列分别为：

X₀={x₀（k）|k=0，1，2，…，n}（4）

X_i={x_i（k）|k=0，1，2，…，n}（5）式中n为序列中因素的個数，x₀（k）和x_i（k）分别为x₀与x_i在第k点的数值。

2）求灰色关联度

点x₀（k）与x_i（k）的关联系数用下式表示：

γ（x₀（k），x_i（k））=式中ρ为分辨系数，常取ρ=0.5;|x₀（k）-x_i（k）|为点距离;为二级最小差值;为二级最大差值，它的取值既根据主行为序列x₀和比较序列x_i之间的关系来决定，还取决于别的标准模式x_j，i≠j。

3）灰色关联排序

令x为灰色关联序列集：γ（x₀，x_i）为主行为序列x₀与比较序列x_i的灰色关联度，若将γ（x₀，x_i）從大到小排序，γ（x₀，x_i）越大，灰色关联程度越高，该排序也反映了不同序列相近程度[13]。

3 基于MRSVD与灰色理论的供输弹故障诊断研究

3.1 信号采集

本文以某供输弹系统为研究对象。通过对该供输弹系统的结构特点以及常见的故障模式进行研究分析之后，本次实验采用32通道LMS系统在实验现场进行信号采集，采样频率设置为25600Hz，布置了6个三方向的ICP型振动加速度测点以及2个声级测点。表1为各测点位置说明表，图2现场搭建测试系统图，图3为测点位置示意图。

3.2 试验记录及故障现象

由于该型号火炮进行了多种射速的试验，而且在出现射速降低的故障后进行了结构改造，基于该试验条件，选择450发/min射速下进行研究，因为在该射速下采集到了相对完整的信号。本文使用振动测点3所采集的数据进行分析。图4为40连发射击时间间隔统计图，图5为40连发振动测点3（x方向）振动信号全程时域图。

3.3 实测信号MRSVD微弱特征提取

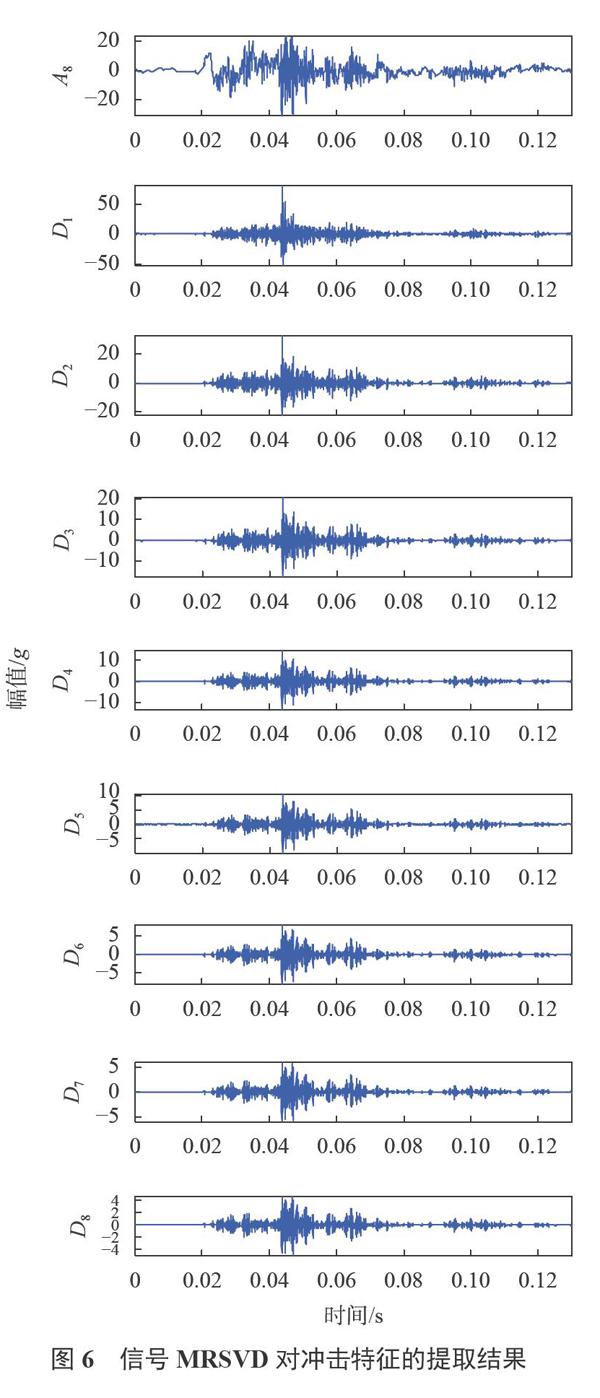
本文对所采集的供输弹系统信号进行奇异值计算，选取前100个奇异值进行分析，可见奇异值差异主要集中在前8个数值，因此对信号进行8层分解得到9个信号，分别是一个相似信号Ag和8个细节信号D₁～D₈，反应了信号的主体概貌和细节特征，然后提取分解信号的能量特征。选择一发振动信号示例，如图6所示。

对于MRSVD分解的不同尺度的信号提取其能量值并进行归一化处理。针对选取的测点和正常、恶化中、故障这3种工况，通过对信号进行奇异差分谱层数优选[14]，然后运用MRSVD理论进行8层分解，最后提取分解信号的能量特征值。选取一个样本的能量相对值作为示例如图7所示。

图中第1分量代表相似信号A₈的相对能量值，第2～9分量分别代表8个细节信号D₁～D₈的相对能量值。由图可知，针对测点不同工况，提取的能量值在相似信号和不同细节信号中具有一定的差异，能够反映供输弹系统不同的状态信息。

3.4 灰色关联分析

针对所采用的试验数据，2连发、6连发为恶化中状态，60连发、80连发为正常状态，40连发为故障状态。为了获取主行为序列，根据本次试验信号采集的情况进行分类，最终选取正常状态60连发数据、恶化中状态的两次6连发数据、故障状态40连发数据来进行分析：每种工况选择5个样本作为测试样本，其余样本定义为训练样本，对训练样本求取平均值可以得到主行为序列，标准模式向量如表2所示，然后计算各个测试样本与标准模式之间的关联度，灰色关联度诊断结果如表3所示。

在表3中，每一个数值都代表待测量和标准量的关联度大小，通过对关联度的排序，选择每种工况的最大关联度值为该工况所属的类型。经过灰色关联度诊断分析，在15个测试样本中，振动测点3诊断出13个，振动测点3准确率约为86.7%。

4 结束语

本文基于MRSVD与灰色理论的方法对供输弹系统进行故障诊断，将提取的测点所对应的MRSVD能量特征进行灰色关联度分析，实验结果表明，振动测点3准确率较高，诊断结果的准确率约为86.7%，并准确地实现对供输弹系统多种故障模式的分析和诊断。本文提出的方法为供输弹系统的发展提供了依据，将该方法应用到供输弹系统故障的分析诊断中是一种有益、可行的尝试。

参考文献

[1]李勇.某供输弹机供药机构的可靠性研究[D].南京：南京理工大学，2017.

[2]付志敏，潘宏侠，许听，等.基于PCA-KLD的供输弹系统早期故障识别[J].机械设计与研究，2018，34（2）：192-195.

[3]赵建，张友鹏，赵斌.基于奇异值分解理论的钢轨断裂检测方法[J].计算机工程与应用，2018，54（9）：243-250.

[4]李葵，范玉刚，吴建德.基于MRSVD和VPMCD的轴承故障智能诊断方法研究[J].计算机工程与应用，2016，52（8）：153-157.

[5]张弢，王金波，张涛，等.基于灰色理论的复杂系统多故障模糊诊断[J].北京航空航天大学学报，2017，43（9）：1832-1840.

[6]杨金宝，梁勇，曹现宪一种基于灰色理论一隐马尔科夫模型的装备故障预测方法[J].舰船电子工程，2018，38（8）：128-132+145.

[7]许海伦.基于电流信号分析与小波一支持向量机的火炮自动装填系统故障诊断研究[D].太原：中北大学，2013.

[8]BHATNAGAR G，SARA A，WU Q M J，et al.Analysis andextension of multiresolution singular value decomposition[J].Information Sciences，2014，277：247-262.

[9]王建国，李健，万旭东.基于奇异值分解和局域均值分解的滚动轴承故障特征提取方法[J].机械工程学报，2015，51（3）：104-110.

[10]李明晓，刘增力.MRSVD-EMD方法在滚动轴承故障诊断中的应用[J].软件导刊，2018，17（5）：138-141.

[11]谢延敏，王新宝，王智，等.基于灰色理论和GA-BP的拉延筋参数反求[J].机械工程学报，2013，49（4）：44-50.

[12]杜尊峰，朱海明，唐广银.基于灰色理论的海上风电机组齿轮箱故障模式及影响分析[J].水利水电技术，2017，48（2）：165-169+164.

[13]ZHANG Z C，CHEN L.Analysis on decision-making modelof plan evaluation based on grey relation projection andcombination weight algorithm[J].Journal of SystemsEngineering and Electronics，2018，29（4）：789-796.

[14]于泽亮，贺德强，谭文举，等.基于EMD和奇异值差分谱理论的列车齿轮箱故障诊断研究及实现[J].机械设计与制造，2018（9）：152-155.

（编辑：莫婕）