基于Lamb波的风电叶片复合材料声发射源定位研究

张鹏林 杨超 董拴涛 田宁

摘要：声发射波在风电叶片薄板结构中传播时产生的多模态效应及频散现象使得波速的测定较为困难，导致声发射源定位误差过大。针对以上问题，从声发射波传播的物理机制出发，利用完备总体经验模态分解（CEEMD）结合Lamb波理论对风电叶片复合材料在不同应力状态下产生的声发射波进行断铅实验研究。研究结果表明：作用于叶片薄板结构的应力方向不同，将会产生不同频率、不同声速的应力波。垂直应力主要激发出弯曲波，该波波速较低（约1357m/s），幅值衰减较快，频率主要集中于50kHz左右;平行应力主要激发出扩展波，该波波速较高（约3634m/s），幅值衰减较慢，频率主要集中于150kHz左右。扩展波无频散效应且衰减较慢，更加适合风电叶片薄板结构声发射源定位。

关键词：风电叶片;CEENID;Lamb波;声发射源定位

中图分类号：TP391 文献标志码：A 文章编号：1674-5124（2019）07-0140-07

收稿日期：2017-11-12;收到修改稿日期：2018-01-03

作者简介：张鹏林（1973-），男，甘肃白银市人，副研究员，博士，主要从事无损检测、无损评估等方面的研究。

0 引言

风电叶片复合材料具有比强度、比模量高及抗疲劳性能好的特点，近年来被广泛应用于风电叶片的制造[1]。叶片是风力机组获取风能的关键部件，然而，受制造条件约束，叶片常易出现脱胶、分层、纤维断裂和基体开裂等缺陷[2]。在使用过程中，具有该类缺陷的叶片在苛刻的自然环境及复杂应力状态下，常常发生失效，导致整机产生破坏。因此，研究叶片复合材料的损伤对于确保叶片及风力机组的长期可靠运行具有重要意义。

声发射检测是一种新型的无损检测技术，对动态缺陷较為敏感，可有效监测纤维增强复合材料损伤失效过程[3]。一般而言，通过声发射信号的分析，能够实现对声发射源的准确定位和定性。然而，由于风电叶片结构本身的不规则，在传统定位方法中单纯采用纵波或者横波进行线性和平面定位会产生较大误差。此外，对于风电叶片薄板结构，当其厚度与声发射信号波长处于同一数量级时，在薄板中传播的横波和纵波也会在板的上下表面相互作用叠加形成一种特殊类型的波—Lamb波[4]。作用于薄板的平行应力主要激发出Lamb波中的扩展波，其波速较高，无频散效应，适合于叶片薄板结构声发射源定位。

使用Lamb波进行定位的相关研究如Wang[5]利用Lamb波理论对金属铜管的声发射源进行了定位，但使用短时傅里叶变换处理信号也意味着忽视了信号的非平稳，非线性特性;Davoodi[6]利用小波变换和CTFS方法在考虑Lamb波的影响下对金属薄板上模拟声发射源进行了准确定位，但目前对于风电叶片及复合材料声发射源定位的研究则相对较少。相关研究有：周伟[7]在忽略声发射波的频散现象和多模态效应前提下对叶片复合材料短距离内声发射信号衰减进行了研究，但在单向板中定位效果较差;袁洪芳[8]通过小波定位研究了风电叶片的裂纹定位，但没有考虑Lamb波的影响;于金涛[9]分析了碳纤维材料中产生不同Lamb波的衰减特性，但没有给出不同模态Lamb波的衰减特性。唐军君[10]利用小波分析研究了碳纤维复合材料中断铅信号的lamb衰减特性，给出了不同类型波的波速和衰减特性，但没有对材料声发射源进行定位研究。

基于此，通过断铅法中不同激励获得了风电叶片复合材料层合板中不同传播模式的声波，之后利用CEEMD方法分离出了Lamb波的不同模式，对信号模态进行了衰减研究，并将其结果初步应用于了叶片复合材料声发射源定位研究。

1 基本理论

1.1 完备总体经验模态分解（CEEMD）

完备总体平均经验模态分解（CEEMD）是一种适合于非平稳、非线性信号的自适应分解方法[11]O相比小波分析，CEEMD方法避免了小波分析中小波基函数选取的困难和海森堡不确定原理的约束，使得CEEMD方法对信号的处理更加真实，并且处理后的信号在时域和频域能同时达到最佳分辨率。相比EMD分解，CEEMD通过添加高斯白噪声较好地消除了单纯使用EMD分解信号时产生的模态混叠和端点效应[12]。

CEEMD分解的具体步骤如下：

1）对原始信号y（t）添加等幅反向随机高斯白噪声，过程如下：

Y₁（t）=y（t）+f_i（t）（1）

y_-1（t）=y（t）-f_i（t）（2）其中y₁（t）和y_-1（t）分别为加入高斯白噪声后的复合信号，f_i（t）为随机高斯白噪声信号。

2）用EMD算法对复合信号进行分解，结果如下：

r₁（t）=y₁（t）-g₁（t）（3）

r_-1（t）=y_-1（t）-g_-1（t）（4）

3）重复步骤1）和2）直到残余量不能被分解为止。此时将得到的IMF分量求其均值并将该均值作为IMF分量的平均结果如下：

1.2 Lamb波理论

当被检结构为板状结构且其厚度和声发射波的波长处于同一数量级时，此时板中传播的横波和纵波会相互作用叠加形成特殊类型的平面应力波-Lamb波[13]，Lamb波具有二维特性，相比三维体波，衰减较小，且由于含有声发射源的特性，常被用于检测行业。根据质点振动位移的方向，Lamb波分为扩展波（对称波）和弯曲波（反对称波），波速依赖于板厚、频率、模式的阶数以及材料的性能等[14]。一般情况下，噪声和非声发射信号不产生Lamb波特征，而对于有用信号，不同的声发射物理过程产生的信号在Lamb波上的模态一般不同[15]。因此，可通过基于产生的声发射信号的物理机制进行模态分析，在一定程度上对声发射源进行定位和类型识别。

2 实验研究

2.1 实验方案

实验仪器采用SAEU2S集中式多通道声发射仪，传感器为谐振式通用SR150M型传感器，谐振频率150kHz，所用材料为按照[0/90°]纤维布多层铺设而成的各向异性风电叶片复合材料，尺寸700mm×700mm×4mm，声发射仪参数设置如表1所示。

实验中共采用4组声发射传感器，传感器呈直线布置，每个传感器相隔100mm，分别记为1^#、2^#、3^#、4^#，声发射激励源距1^#号传感器距离200mm。实验采用断铅信号模拟声发射源，笔芯为直径0.5mm的田3石墨铅笔芯，伸长量2.5mm。声发射传感器布置示意图如图1所示，实验现场照片如图2所示。

2.2 Lamb波的识别及其分离

实验利用断铅法分别在叶片材料薄板边缘进行垂直断铅和水平断铅以获得不同方位激励的声发射时域信号，图3为4^#传感器接收到不同激励作用时产生声发射时域波形图。

从图3（a）可以看出，水平断铅获得的信号为突发型信号，信号幅值约为0.35mV，呈幂指数衰减，在1.3ms后衰减至0，持续时间相对较长;同理，在图3（b）中可以看出，垂直断铅获得的信号在采集时间段内近似于突发型信号，最高幅值约为0.7mV，衰减较缓慢，持续时间约2ms。但进一步观察可以发现：垂直断铅信号在时域上可分为两个波包，在0～0.5ms内首先到达的快波波包波形和水平断铅得到的信号的波形基本相似，幅值约为0.6mV，之后，在0.5～2ms内到达的慢波波包波形和先前到达的快波波形明显不同，波形呈先增大后减小的趋势，幅值相对较大，约为0.7mV，衰减也相对较快，在衰减过程中且有多种波形混雜现象出现。

为研究不同激励产生的声发射信号的特性，对原始信号进行三层小波包分解，小波函数采用正交小波db10。不同激励方式产生的信号经过三层小波包分解后的小波频系数能量谱图如图4所示。

由图4可以看出，水平断铅激励产生的声发射信号，各频段所含能量在整个频段内分布不均匀，根据奈奎斯特采样定理及格雷码顺序，可知其信号能量主要集中于（3，0）、（3，1）及（3，3）频带内，所占能量比例分别为16.75%、26.45%及31.05%，对应频率范围分别为0～62.5kHz、62.5～125kHz及125～187.5kHz。而垂直断铅产生的声发射信号各频段能量则主要集中于（3，0）和（3，3）频带中，所占能量分别为57.87%和21.69%。频率分布范围为0～62.5kHz和125～187.5kHz。对比上述结果可以发现，随着激励方位的改变，不同信号能量分布发生变化，当激励从平行向垂直转变时，其能量也向低频段发生转移，频率也向低频段发生转移。根据Lamb波理论，该现象的发生主要是不同方向激励产生不同类型的波所导致。

为进一步得到不同激励的信号频率的具体分布状况，对上述不同激励产生的信号（降噪处理后）进行希尔伯特变换，其对应的功率谱如图5所示。

由图5（a）可看出，当叶片复合材料薄板主要承受水平激励作用时，信号中存在两种频率成分，频率分布集中于50kHz和150kHz附近，其中频率为150kHz部分信号能量占主要部分;同样，在图5（b）中可以看出，当叶片复合材料薄板主要承受垂直激励作用时，信号中频率也分布在50kHz和150kHz附近，但主要信号能量集中于50kHz附近。对比图5（a）和图5（b）可以发现：对于风电叶片复合材料薄板，当承受不同方位激励作用时，声发射波频率成分基本类似，功率谱基本无边带族现象产生，但不同激励作用产生的功率谱频带分布有所不同，主要集中频段存在较大差异。

为确定在不同激励条件下，叶片复合材料薄板中声发射波的时频特性，对声发射波进行CEEMD分解。实验中添加白噪声的标准差取原声发射信号标准差的0.2倍，迭代次数取100。通常，CEEMD分解的各个IMF分量分别对应原始信号的各实际组分。然而，受环境因素所限，实验中总会引入干扰信号成分。依据统计学理论，CEEMD分解的各实际IMF分量和原始信号之间存在较大关联性，而干扰信号和原始信号之间关联性则相对较小。为消除干扰信号对信号重构的影响，本实验通过比较IMF分量与原信号的互相关系数，从而对IMF分量进行有效筛选。

IMF分量和原始信号之间关系定义如下：式中：g_a（t）——IMF分量和原始信号的互相关系数;

N——信号长度;

n——分量个数;

τ——时间间隔。

之后定义其互相关系数，计算不同激励声发射信号经过CEEMD分解后的IMF分量与原信号的互相关系数如图6所示。

从图6（a）中可以看出，水平激励产生的信号经过CEEMD分解后得到11个IMF分量和一个残余分量，采用互相关系数法发现，相关系数较大IMF分量主要集中在前6个IMF分量;同理，在图6（b）中也可以看出，垂直激励产生的信号经过CEEMD分解后也得到11个IMF分量和一个残余分量，而其真实信号IMF分量则主要集中在前8个IMF分量，之后分别对经过IMF筛选的主要nVIF分量进行希尔伯特变换，得到不同三维田IT如图7所示。

从图7（a）可以看出，在水平激励瞬间，首先产生150kHz的高频信号.，经过约40μs后，产生50kHz的低频信号，根据Lamb波理论，高频信号为扩展波的最低阶（S₀）模式，低频信号为弯曲波的最低阶（A₀）模式，依据波的时间和距离求得扩展波波速约为3634m/s，弯曲波波速约为1357m/s;由图7（b）可看出在垂直激励瞬间，首先产生150kHz高频信号，其为扩展波最低阶（S₀）模式，经过约55μs产生50kHz的低频信号为弯曲波的最低阶（A₀）模式。结合原始波形图可推知两种波形均含有50kHz的A₀模式和150kHz的S₀模式，不同模态存在主要是由于应力作用时并非完全水平和垂直造成。

2.3 不同模态信号衰减特性研究

由于幅度相比能量更能直观反映信号衰减特性且不受门限的影响，因此常被用于声发射源的类型鉴别及信号衰减测量。通过对幅值进行不同模态声发射波的衰减研究，为声发射源精确定位选择合适的统一模态波。

实验以1^#传感器作为参考，分别进行绝对衰减和相对衰减性能测定。定义声发射信号相对衰减率为

Z_i=201g（A_i/A₁）（7）其中A_i为第i个传感器的幅值。

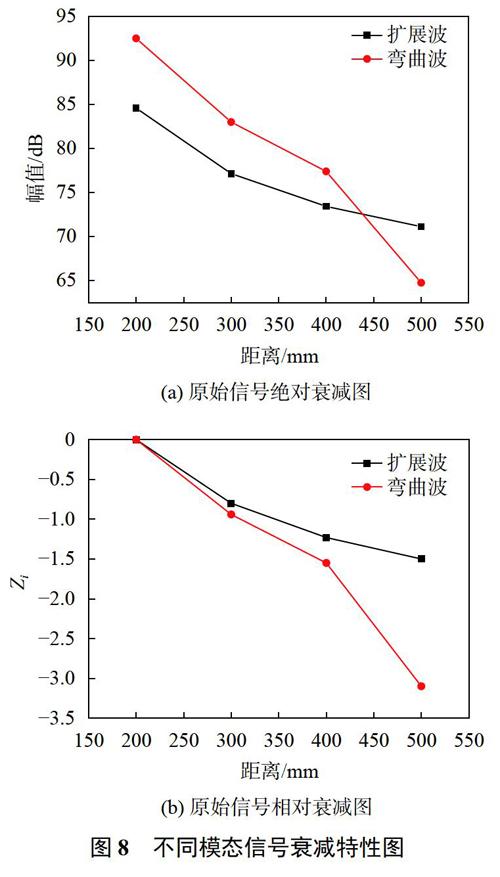
由于叶片复合材料薄板在承受不同方向激励时主要产生两种不同模态的波，且其频率相差较大，因此采用带通滤波方式为主（设定上下截止参数）结合Matlab中数字滤波方法剔除电子噪声及铅芯摩擦噪声，得到单一形态的模态波。不同模态信号衰减特性实验结果如图8所示。

由图8（a）可以看出，在衰减过程中，相比低频弯曲波，高频的扩展波信号衰减趋势相对较小，但由于幅值差异，为排除外在因素干扰，研究其相对衰减特性。图8（b）为不同信号相对衰减过程，从图中可以看出，衰减过程中高频的扩展波信号近似呈指数线性衰减特性，相比低频弯曲波，衰减曲线斜率绝对值较小，曲线平均斜率绝对值为0.49，低频弯曲波衰减曲线平均斜率绝对值为1.02，相比之下，在单位距离内高频的S。信号衰减更为缓慢，且相对弯曲波衰减线性较好。长距离叶片衰减研究中，就信号有效接收而言，适合衰减定位研究应用。

2.4 声发射源定位研究

声发射源定位实验示意图如图9所示。

分别采用扩展波和弯曲波进行定位。常见声发射源中既含有水平分量又含有垂直分量，在图9所示位置进行30°断铅实验。每组实验进行3次。采用时差定位法，以1^#传感器为参考，以2^#，3^#，4^#传感器距离断铅位置300，400，500mm为标准值，通过测得的波速以及声发射信号分别到达2^#，3^#，4^#传感器的时间差和距离分别计算声发射源的位置。由于噪声的影响，需要对原始信号进行阈值去噪后进行信号重构。实验所测数据如表2和表3所示。

从表2和表3可以看出，当采用弯曲波进行定位时，在有效信号范围内，随着距离增大，产生较大误差且误差呈增加趋势，这是由于随着距离增加弯曲波的频散效应增加所致。同时考虑到叶片本身的结构较大，外形不规则，叶片声发射检测中采用这一方法不能准确地确定声发射源的有效位置;而采用扩展波进行定位时，在一定范围内误差较小，定位准确，而随着距离在有效范围内的增加，其误差呈现减小趋势，这是由于随着距离的增加，模态在时域上的分离较为容易，且不存在频散现象，使得时差测量更加精确。因此，在风电叶片声发射检测中可通过时差定位结合Lamb波理论综合分析，从而对叶片声发射源进行有效定位。

3 结束语

通过对风电叶片复合材料进行不同方向激励获得不同类型的Lamb波信号，结合CEEIVID方法对信号进行分解，通过研究Lamb波中不同类型模态波衰减特性，将其应用于声发射源定位研究，得到结论如下：

1）当风电叶片薄板承受水平激励时，波形中以扩展波为主，波速较大，约为3634m/s，且其频率较高，集中于150kHz左右，幅值衰减较慢。

2）当风电叶片薄板承受垂直激励时，波形中以弯曲波为主，波速较小，约为1357m/s，其频率较低，主要集中于50kHz左右，幅值衰减较快。

3）在单位距离内，扩展波衰减曲线平均斜率绝对值为0.49，弯曲波衰减曲线平均斜率绝对值为1.02，扩展波衰减较为缓慢。该研究不但为Lamb波的应用提供了思路，也为风电叶片缺陷的现场监测提供了一定的参考依据。

4）在叶片声发射检测中，采用低衰减，无频散的扩展波进行叶片声发射源定位更加准确。

参考文献

[1]周伟，孙诗茹，冯艳娜，等.风电叶片复合材料拉伸损伤破坏声发射行为[J].复合材料学报，2013，30（2）：240-246.

[2]MAHMOOD M S，ROHAM R.Simulation of fatigue failurein a full composite wind turbine blade[J].CompositeStructure，2006，74（3）：332-342.

[3]李海斌，阳建红，刘承武，等.复合材料随机渐进失效分析与声发射监测[J].复合材料学报，2011，28（1）：223-229.

[4]张海燕，他得安，刘镇清，等.层状各向异性复合板中的兰姆波[M].北京：科学出版社，2008.

[5]WANG C，JOE A Y H，LIN L，et al.Guided wave modedispersion of transient acoustic emission on copper pipes—Itsvisualisation and application to source location[J].Mechanical Systems and Signal Processing，2016，70（71）：881-890.

[6]MOSTAFAPOUR A，DAVOODI S，GHAREAGHAJI M.Acoustic emission source location in plates using waveletanalysis and cross time frequency spectrum[J].Ultrasonics，2014，54（8）：2055-2062.

[7]周伟，田晓，张亭，等.风电叶片玻璃钢复合材料声发射衰减与源定位[J].河北大学学报，2012，32（1）：100-104.

[8]袁洪芳，周璐，柯细勇，等.基于声发射信号的风机叶片裂纹定位分析[J].计算机工程与设计，2011，32（1）：320-323.

[9]于金涛，丁明理.复合材料声发射信号传播特性实验研究[J].电机与控制学报，2012，16（8）：107-112.

[10]唐军君，卢文秀，李峥，等.碳纤维复合材料层合板Lamb波衰减特性研究[J].振动与冲击，2016，35（6）：75-79.

[11]YEHJR，J S，HUANG N E.Complementary ensembleempirical mode decomposition：a novel noise enhanced dataanalysis method[J].Advances in Adaptive Data Analysis，2010，2（2）：135-156.

[12]LEI Y G，LIN J，HE Z J，et al.A review on empirical modedecomposition in fault diagnosis of rotating machinery[J].Mechanical Systems and Signal Processing，2013，35（1-2）：108-126.

[13]林莉，李喜孟，李繼承.超声无损表征薄层结构研究进展[J].无损探伤，2006，30（5）：1-4.

[14]沈功田.声发射检测技术及应用[M].北京：科学出版社，2015：72-73.

[15]耿荣生，沈功田，刘时风，等.模态声发射一声发射信号处理的得力工具[J].无损检测，2002，24（8）：341-345.

（编辑：刘杨）