外加磁场对Q235钢力磁效应影响试验研究

樊清泉 任尚坤 任仙芝 许洋 段振霞

摘要：为研究外加磁场对铁磁材料力磁效应的影响，制作通不同大小直流电的螺旋管作为外加磁场，对带有圆孔缺陷的Q235钢试件进行干扰的静载拉伸试验。结果表明：在地磁场环境中，经去应力退火的试件在没有施加载荷时，初始磁感应强度值趋近于0，磁记忆信号曲线近似水平直线;在施加载荷时，法向磁信号和切向磁信号曲线均发生波动，产生非线性变化;在一定外加磁场范围内，在外加磁场方向和地磁场方向存在差异时，外加磁场与磁记忆信号具有不同的相关性，同向外加磁场越大时，应力集中区磁记忆信号愈加明显;外加磁场的大小不改变其法向和切向磁记忆信号曲线变化规律，但影响其磁感应强度B值和斜率K值的大小，并且对在弹性阶段和塑性阶段法向和切向磁记忆信号的影响也存在差异性。

关键词：金属磁记忆;外加磁场;静载拉伸;力磁效应

中图分类号：TG115.28 文献标志码：A 文章编号：1674-5124（2019）06-0046-08

收稿日期：2018-07-20;收到修改稿日期：2018-08-25

基金项目：国家自然科学基金（51261023）

作者简介：樊清泉（1991-），男，河南平顶山市人，硕士研究生，专业方向为金属磁记忆的研究。

0 引言

金属磁记忆检测技术作为无损检测方面的新型检测技术[1]，相比于传统漏磁检测主要运用在压力容器、铁路轨道、飞机起落架等化工和交通方面[z-;金属磁记忆检测技术目前能广泛应用于对铁磁性材料进行快速、早期的检测，具有其他检测所不具有的优势[8-10]。该项技术由俄罗斯科学家DUBOV教授[11]于1994年首次提出这个概念，其原理实质上是磁弹性和磁机械效应共同作用的结果[12]，磁记忆检测技术就是利用了铁磁构件在地磁场环境中，受到工作载荷的作用，残余磁性发生改变和重新分布，并在应力消失后得到了保留，从而能成为铁磁构件无损评价的早期诊断方法。目前多以研究应力和磁信号之间的对应关系[13-15]，通过磁信号的变化来对试件早期损伤进行预判，但是相比其他传统无损检测技术需要外加激励磁场[16]，金属磁记忆是不需要外加激励磁场的，因此外磁场强度对磁记忆信号的影响至关重要[17]，在不同的环境磁场中测得的磁信号具有显著差异[18-19]。以上多数只是单一的改变外部磁场环境，对其法向磁记忆信号变化规律进行分析，对其微观作用机制，以及切向磁记忆信号变化规律却很少提及。

為充分了解外加磁场对铁磁材料力磁效应变化规律的影响，本文将采用静载拉伸试验，结合理论知识，对法向和切向磁场信号曲线变化规律及力磁效应的微观机制进行分析，并且结合数学理论分析，充分验证应力与磁记忆信号之间的相关性，分析对比弹性阶段和塑性阶段外加磁场对力磁效应的影响，为通过运用磁记忆检测技术更好地进行早期诊断提供依据。

1 试验方案

1.1 实验设备

本文采用直流稳压电源进行单路输出，外加磁场设备采用自制螺线管，直径50mm，漆包线直径0_67mm，蛤靛戈管长180mm，有效长度范围40160mm，漆包线匝数400匝，共两层。磁记忆信号采集将采用由美国Lake Shore公司设讨生产的421 Gaussmeter弱磁场测量仪，测量范围为10～30T;测量误差为±02%。

1.2 试验方法

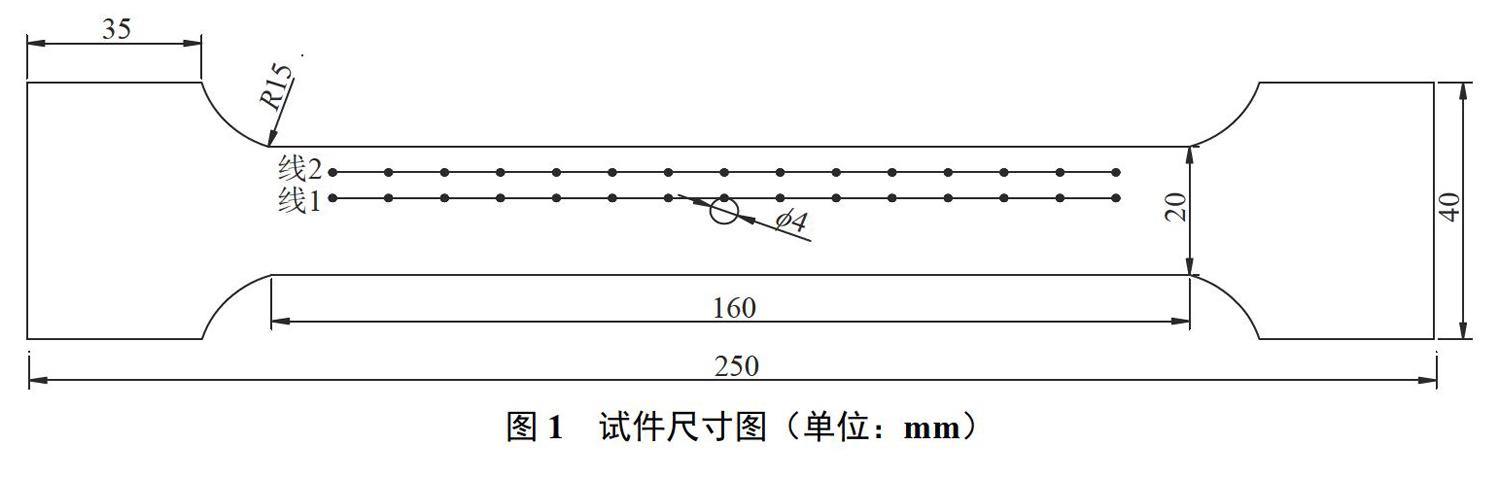
本实验材料选用Q235碳素钢，为确保试验结果的可靠性，对每种试块均预备加工试块2块进行试验，总计预备12块圆孔缺陷试件，编号1～12。实验前，对试件进行去应力退火试验，消除试件的内应力，然后用砂纸对试件表面进行打磨处理。试件尺寸如图1所示，试件厚度为3mm。

实验前对编号为12的试件利用INSTRON（8801）电液伺服疲劳试验机进行静载拉伸试验，测量其屈服强度287MPa。数据采集时为减小地磁场的影响，试件东西方向放置，分别在距离圆孔中心2mm和6mm处设立路径1和路径2，路径采集个数均为15个点，从左到右依次记为采样点1，2，3，…，14，15，每两个点间隔8mm，其中第8个点位于路径中心处。将试件放在拉伸机上的螺线管内，并依次通上-30mA、0mA（地磁场环境）、60mA、150mA和300mA直流电产生外加磁场一80A/m，地磁场、160A/m、400A/m和800A/m，正、负分别表示磁场方向向下和向上。试验时将试件施加到固定载荷取下，进行离线测量，拉伸速率为1mm/min，重复操作，直到试件断裂，并对断裂后试件进行再次测量。

2 实验结果及分析

2.1 地磁场环境下的力磁效应分析

对试件1在地磁场下进行拉伸试验，测量采样点的数据进行绘图分析，图2（a）、图2（b）分别为地磁场下测得的法向磁记忆信号和切向磁记忆信号强度曲线。

如图2（a）所示，当拉应力o-为0时，法向磁记忆信号基本保持在水平线上，维持在B=OT附近。随着拉应力o-的增加，法向磁记忆信号曲线在采样点1～5和11～15区域呈斜直线，采样点6～10区域呈S形，呈逆时针方向转动，且△B=B₈-B₇总体呈现增加趋势，圆孔附近斜率K=△B随之不断增加。如图2（b）所示，在无应力时，切向磁记忆信号趋向于一条直线，维持在B=OT附近。当应力σ逐渐增加时，切向磁记忆信号曲线在采样点1～5和11～15区域呈水平直线，采样点6～10区域切向磁记忆信号曲线出现峰值，呈三角形，随着应力的增加，以采样点6～10的采集数值构成的三角形面积随之增大。

弹性阶段，法向和切向磁记忆信号变化曲线非线性都不是很明显，S形和三角形变化不大;塑性阶段，在应力的作用下影响较大，非线性较为明显，S形和三角形变化较大。

分析其出现弹性和塑性阶段曲线分布差异的原因，可能与材料初期的退火处理及后期应力磁化有关。铁磁材料经热处理可基本消除材料残余应力，此时材料内的磁筹组织大体呈现出无序排布的状态，各磁畴的磁矩相互抵消，整个物体总磁矩为零即基本不呈现磁性，表现为无应力时磁感应强度B≈OT。弹性变形阶段，在施加拉应力后，材料内的磁筹组织由无序排布的状态向有序状态分布，磁畴组织的转动使内部磁畴取向趋向一致，显示一定的磁性，虽然将试件卸载后，应力恢复，但是磁畴组织的转动所产生的磁性还是被部分保留下来，表现为使其材料表面的磁场发生了改变[20]，测得的磁感应强度数值曲线上移，数值变大，沿检测方向呈现为非线性变化;在塑性变形阶段，材料进行加载并卸载，加载时的应力或者卸载后的残余应力导致材料发生应力磁化。根据Ludwik定理[21]的定义，在塑性阶段施加拉应力后：

σ_F=σ_f-σ_y=Gε_pⁿ（1）式中：G、n——常数，与材料性质和形状有关;

ε_p——塑性形变量，%，

σ_f——加载应力，MPa;

σ_y——材料屈服应力，MPa;

σ_F——应变硬化应力，MPa。

塑性变形使材料内位错密度增大，导致材料钉扎点增多。晶格滑移形变，进一步影响和改变了材料内磁畴的形状和尺寸大小，导致其微观磁畴结构发生可逆和不可逆运动，从而影响磁记忆信号。

2.2 外加磁场环境下的力磁效应分析

取其余试件编号为3、5、7、9依次置于通有直流电的螺线管内，进行静载拉伸，测得磁感应强度曲线分布如图3～图6所示。

如图3（a）、图4（a）、图5（a）、图6（a）所示，从-80A/m到800A/m在施加应力前，法向磁记忆信号分布曲线均呈现一条水平直线，无明显非线性变化。随着应力载荷的增加，法向磁记忆信号逆时针方向转动。弹性阶段，AB变化幅度较小，即法向磁记忆曲线的非线性特征变化不大;在塑性阶段，AB变化幅度较大，即磁记忆曲线的非线性特征变化明显，呈现跳跃式变化;在采样点7和8之间的位置，均出现B=0T即过零点现象。由图3（b）、图4（b）、图5（b）、图6（b）所示，在-80A/m到800A/m在施加应力前，切向磁记忆信号分布曲线呈现一条水平直线，弹性阶段随着应力的增加，测得磁感应强度B相较无应力时均增加，在中间应力集中部分出现较小的非线性变化，即出现方向朝上的峰值，且峰值大小随应力增加而逐渐增大。塑性阶段，随着应力增大，峰值区域的三角形面积变大。

2.3 断裂时磁场强度变化分析

从图7（a）可以看出，在试件断裂后，法向磁记忆信号均发生偏转，呈现倒S形。在外加磁场不断增大的前提下，磁感应强度值最高点和最低点的|B|增大。图7（b）显示试件断裂后，切向磁感应强度出现的三角形方向發生转变，且随着外加磁场强度的增加，倒三角形面积越大。将在同向和反向磁场测的法向和切向磁记忆信号分析可知，在外加磁场为-80A/m时，磁感应强度曲线几乎呈现水平状态，相比于其他外加磁场强度B≥0A/m的变化幅度，|B|反而变化很小，本应该在此增大的|B|，反而比地磁场下的变化更小，线性较平缓，应力集中区也没有出现很大的非线性变化。因此在外加磁场强度不断增大的情况下，方向和地磁场同向时，施加磁场与地磁场进行叠加，让非线性更加明显，磁信号更强，便于识别应力集中;相反的，方向不一致时，施加磁场与地磁场进行相互抵消一部分，磁信号稍弱。这对于不需要外加激励磁场，单单依靠地磁场进行检测的金属磁记忆具有重要的指导意义。

2.4 数据分析

由于各磁场环境下，一定拉伸应力阶段下的的法向和切向磁记忆信号变化规律趋向一致，因此以下试验将以弹性阶段拉应力σ为83MPa和塑性阶段拉应力σ为333MPa统计的数据为例，并且采用均值和标准差进行数值计算分析。

通过图8（a）和图9（a），图8（b）和图9（b）对比发现，在拉应力σ为333MPa的作用下的磁信号，均呈现和σ为83MPa一样的变化规律，但是数值变化幅度较大。以图9为例，在图9（a）中，进入塑性阶段，在外磁场强度增加的情况下，法向磁记忆信号且呈逆时针方向旋转。图9（b）中切向磁记忆信号数值随应力增加，且圆孔附近采样点6、7、8、9测得磁感应强度构成的三角形面积增加较大，但是峰值出现的位置几乎不发生改变。始终显示出和图8一样的规律，说明外加磁场在塑性阶段只对其磁记忆信号大小产生影响，特别是在外加磁场增加到400A/m、800A/m时，变化比较明显。

设定n为高斯计对σ下采集的数据样本数，这里取n=15，计为σ误差均值，△B（σ，k）为σ下第k个采样点的磁感应强度，σ取值83MPa、333MPa以及k取磁场分别为-80A/m、地磁场、160A/m、400A/m和800A/m，j=1，2，3，…，14，15。

设B_j（σ，0）为地磁场下在σ时采样点j的磁感应强度，B_j（σ，k）为不同外加磁场下在σ时采样点J的磁感应强度测量值，△B_j（σ，k）=B_j（σ，k）-B_j（σ，0）则表示在外磁场环境为k时，高斯计所测得的磁感应强度与地磁场下所测得的磁感应强度的误差值。

基于以上定义，对σ下的误差均值和误差标准差有以下统计量：

式（2）表示σ误差均值;式（3）表示σ误差标准差。

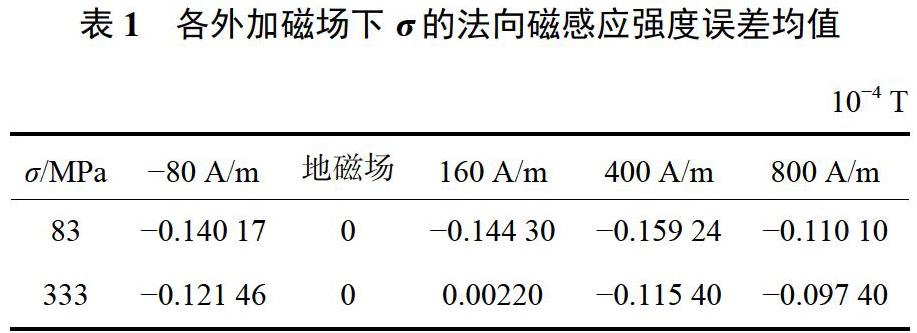
由表1数据可以看出，在σ= 83MPa和σ二333MPa时，外加磁场对其法向磁感应强度均值影响不大，基本上在。附近震荡;表2可以得出外加磁场方向和地磁场方向同向时，σ= 83MPa时的标准差均大于σ=333MPa的标准差，说明弹性阶段外加磁场对法向磁感应强度值的影响要大一些;反向时，则相反。

由表3数据可以看出，在σ= 83MPa和σ=333MPa时，外加磁场对其切向磁感应强度平均值均产生影响，同向磁场下，随外磁场增大而影响越大;表4可以得出，σ=83MPa时的标准差均小于σ= 333MPa的标准差，说明相同外加磁场环境下，塑性阶段较弹性阶段影响较大。且在一定应力不同外加磁场条件下，外加磁场对切向磁感应强度的影响随自身强度的增加影响越大。

3 结束语

以各个固定磁场环境下的法向和切向磁记忆信号变化特征为切人点，研究在不同磁场环境中的力磁耦合关系，并对试件在不同磁场环境中断裂时的磁记忆信号进行了分析，结合数学理论研究可得如下结论：