基于汽车风噪的主动噪声控制系统的研究与设计

袁 军，刘东旭，吕韦喜，王 巍，张 涛

(重庆邮电大学 光电工程学院, 重庆 400065)

在高速公路驾驶过程中，人们可以很强烈地感受到车内的噪声，因此对车内噪声控制的要求越来越高。车辆在不同状态下行驶时，噪声主要包括动力系统噪声、路面噪声和风噪声[1]。汽车在怠速和低速运行时，主要的噪声来自发动机和其他动力系统(如排气系统、进气系统等)。当车速到达50 km/h时，路面噪声会随着车速的增加而增加，并成为车内的主要噪声源。而当车速持续增加，达到100 km/h时，风噪(行驶的汽车与空气有相对运动，运动的空气作用在车身上对车内产生的噪声定义为风噪)开始出现，并逐渐成为汽车的主要噪声源。

汽车风噪的控制可以从车身设计和噪声控制系统这两方面进行。车身设计包括车身整体造型的设计、局部结构与附件的设计和车身密封的设计。噪声控制系统的设计包括主动噪声控制(ANC)和被动噪声控制(PNC)的设计[2]。与传统的被动噪声控制方法相比，ANC系统在低频噪声的降噪、安装的便利、工作性能的稳定、价格成本等方面有着很好的效果[3]。因此，本文将主要从建立车内ANC系统的角度来研究对汽车风噪的控制。

ANC系统作为噪声消除的重要组成部分，其设计中所面临的主要挑战与次级通道相关。当ANC系统的参考噪声信号不实时存在时，次级通道可以在ANC控制器工作之前进行离线建模。然而在汽车高速行驶过程中，风噪信号会始终存在，且次级通道路径可能是时变的，因此本文需要对次级通道在线建模以确保ANC系统的收敛。

次级通道在线建模有两种方法：一种是辅助噪声注入法，一种是反馈法。研究表明[4]：使用辅助随机白噪声注入的方法在主动噪声控制与次级通道在线建模过程之间的独立性、次级路径建模的频带范围、ANC控制器和次级通道建模滤波器的收敛速度以及计算复杂度等方面优于反馈法，因此本文使用辅助白噪声注入法。另外，通过文献[5]可知，辅助白噪声功率、滤波器的步长因子、ANC控制滤波器和次级通道在线建模之间的独立性这3个因素对系统的性能参数有很大影响。

本文第1节主要介绍ANC系统基本原理和FxLMS算法的基本结构；第2节提出改进次级通道在线建模结构的方法；第3节讨论通过仿真噪声信号实现的ANC系统降噪的效果；第4节给出结论。

1 ANC的基本原理和结构

1.1 ANC的基本原理

主动噪声控制(ANC)主要基于声叠加原理，是通过控制扬声器在指定区域发出相对应的消声信号来控制初始参考噪声信号的一种噪声控制方法[6]。如图1所示：参考噪声信号x(n)由噪声源处输入，经过ANC系统处理后产生输出信号y(n)，驱动扬声器发出与噪声信号x(n)频率相同且幅值相反的消声信号，从而达到降噪的效果。误差麦克风用来接收误差信号e(n)并将其送回到ANC中进行自适应调整，达到提高ANC系统降噪性能的目的。

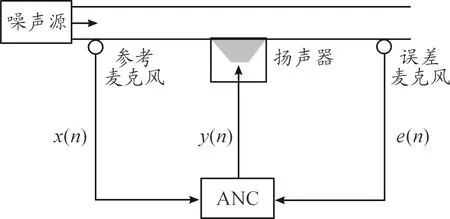
图1 ANC系统

1.2 FxLMS算法的基本结构

目前，ANC系统中使用最流行的自适应算法是滤波x最小均方(FxLMS)算法：当将LMS算法用于ANC系统时，应预估次级通道路径并使参考噪声信号输入到已经估计的次级通道路径中，此过程称为滤波x最小均方(FxLMS)算法[7-8]。在近十几年对FxLMS算法的研究中，Eriksson、Akhtar以及Davari的方法被广泛提及，所以本文对这几种算法结构进行简略分析。

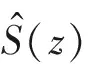
图2 Eriksson的次级通道在线建模方法

Akhtar提出一种在ANC系统次级通道建模过程中对步长因子采取变步长LMS(variable step size LMS，VSS-LMS)算法的在线建模方法[10]。该方法最大优点是有效地降低了主动控制环节和次级通道建模环节的相互影响，从而提高了ANC系统的整体性能，系统框图如图3所示。但该方法没有考虑到次级通道建模信号v(n)对主动噪声控制环节的影响。VSS-FxLMS算法的步长参数μS(n)更新的具体步骤为：

步骤1首先，计算误差信号e(n)和f(n)的功耗：

Pe(n)=λPe(n-1)+(1-λ)e2(n)

(1)

Pf(n)=λPf(n-1)+(1-λ)f2(n)

(2)

步骤2获得2个误差信号功率的比值：

ρ(n)=Pf(n)/Pe(n)

(3)

步骤3步长参数和辅助白噪声功耗计算如下：

μs(n)=ρ(n)μSmin+(1-ρ(n))μSmax

(4)

其中μSmin、μSmax和λ通过多次实验确定。

图3 Akhtar的次级通道在线建模方法

Davari提出了一种对次级通道建模信号进行开关控制的策略[11]。当系统达到稳定状态时停止ANC系统次级通道在线建模，当检测到误差信号发生较大变化时，再次注入建模信号v(n)重新建模，系统框图如图4所示。

图4 Davari的次级通道在线建模方法

辅助白噪声v(n)可以使用式(5)在达到最佳点处停止注入：

μSmax-μS<α

(5)

从图4中可以看出，该条件的有效性可在性能监视模块被控制。经过多次调整分析可以发现，将α设置在10-3～10-5之间会使次级通道建模更加精确。

通过式(6)来监视次级路径的变化：

20log10|f(n)|<0

(6)

如果上述方程的有效性不被满足，则系统重新激活VSS-FxLMS算法并注入随机白噪声重新建模次级通道滤波器。系统在操作过程中不断重复上述过程以适应不断变化的环境特征。

2 提出次级通道在线建模的方法

2.1 主控制滤波器变步长调节

由上面的分析可知，Eriksson提出的次级通道在线建模的困难在于用于次级通道建模的训练信号与控制系统信号的相互干扰会影响建模的收敛速度，从而使控制系统的整体性能恶化。Akhtar提出的方法在最近关于FxLMS算法的研究中获得了较好的性能表现，但是没有考虑次级通道训练信号对主动控制滤波器的影响，且算法中的参数不利于实际应用。Davari改进Akhtar的算法，提出了次级通道在线建模和离线建模相互转换的方案。该方案能受益于巨大方差白噪声带来的次级通道，具有更好的建模精度和收敛速度，然而也会受到由于环境变化使得门限值需要不断调节从而导致ANC系统收敛速度变慢的影响。基于此，本文在上述算法的基础上，将μs(n)的调节方式与主动控制滤波器步长因子μw(n)的调节方式相结合，对主控制滤波器步长因子μw(n)采用变步长FxLMS(CVS-FxLMS)算法，系统框图如图5所示。

图5 改进算法结构框图

由图5可知，用于建模滤波器和控制滤波器的误差信号f(n)由式(7)给出：

f(n)=d(n)-xT(n)ω(n)+

(7)

取Z变换得：

F(z)=[P(z)-W(z)S(z)]+

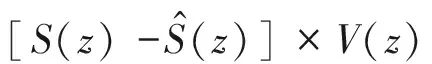
(8)

随着主控制器W(z)不断收敛，在理想情况下次级通道的误差信号f(n)可以收敛到零，此时控制滤波器W(z)达到其收敛的最佳值：

(9)

由式(9)可知：当次级通道建模滤波器S(z)收敛到最佳时，W(z)收敛到其理想解P(z)/S(z)。由W(z)的理想解可知，控制滤波器和建模滤波器是相互影响的，这也是本文提出将主控制滤波器的步长因子和次级通道建模滤波器的步长因子调节方式相结合的理论基础。

为了避免当参考噪声信号x(n)增加时可能导致的ANC系统不收敛，主通道步长因子μw通常被设定为一个很小的值。然而一旦参考噪声信号能量减小时，小的μw值又会降低ANC系统的降噪性能和主控制滤波器W(z)的收敛速度。因此，可以在x(n)减小时采取较大的μw值，反之亦然。主通道变步长算法能在初级噪声信号或者次级通道传递函数突然发生变化时跟踪这种突变，并使ANC系统迅速收敛到稳定状态。

已知：

d(n)=f(n)+xT(n)ω(n)+

(10)

假设期望信号为

d(n)=η(n)+xT(n)ωo(n)

(11)

f(n)=η(n)+xT(n)Δω+vT(n)Δs

(12)

f(n)f(n-1)=η(n)η(n-1)+

η(n)xT(n-1)Δω+η(n)vT(n-1)Δs+

η(n-1)xT(n)Δω+ΔωTx(n)xT(n-1)Δω+

xT(n)ΔωvT(n-1)Δs+ΔsTv(n)vT(n-1)Δs

(13)

由式(12)(13)可知，因为η(n)均值为零且与x(n)和v(n)不相关，所以f(n)的均方误差可以表示为：

E[f(n)f(n-1)]=E[ΔωTx(n)xT(n-1)Δω]+

E[ΔsTv(n)vT(n-1)Δs]

(14)

可见，误差信号相关值正比于建模误差及当前时刻权矢量系数与最佳值之间的差值。随着迭代次数的增加，建模滤波器与控制滤波器逐渐收敛，则误差信号相关值随之减小。因此，根据上面的推导分析，主控制滤波器建模收敛因子μw(n)变步长公式如下：

(15)

该步骤函数以参数α和β的期望值建模，表示为

(16)

其中常数k用于控制α(n)，调节主控制滤波器的收敛速度。

(17)

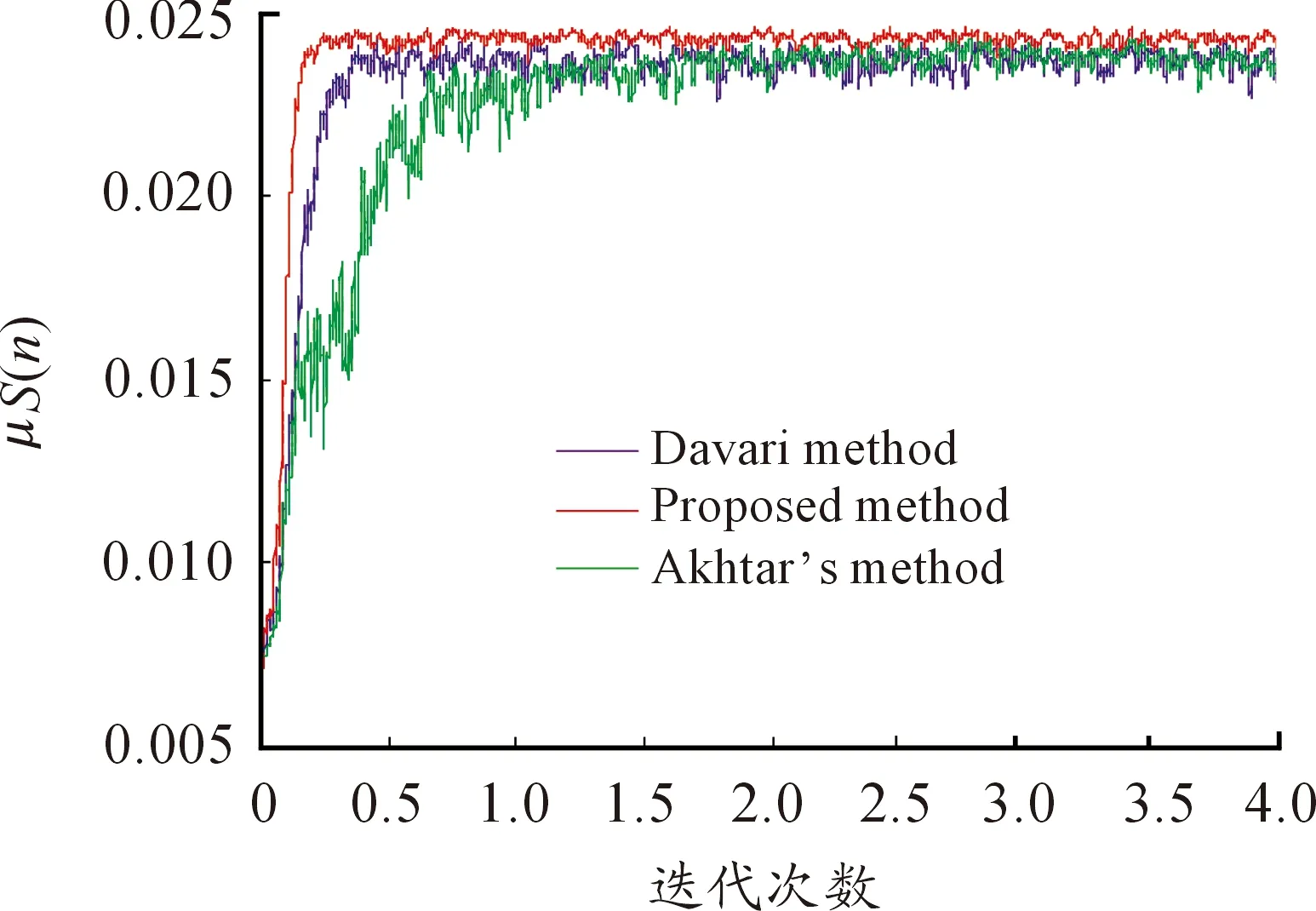
其中常数b0用于确保收敛速度，该因子大小限制为0

VSFxLMS的系统更新方程为

W(n+1)=W(n)+2μw(n)×e(n)×x′(n)

(18)

两个参数α(n)和β(n)是误差率e(n)/e(n-1)的函数。当式(16)中的比率较大时，误差变化较大，CVS-FxLMS算法将处于收敛阶段。如果误差变化率较小，步长u(n)也将较小，从而使算法处于稳定状态。类似地，参数β(n)也起相似的作用。

常数k用于调整α(n)的变化速度。对于较高的收敛速度，k趋向于较小的值。但是为了保持精度，k的值需要更小。参数b0用于确保收敛，但不同的b0值可能影响算法，从而改变ANC系统的降噪性能。当使用该步长函数时，式(18)中所示的滤波器系数的更新方程将是传统FxLMS时的2倍。VSFxLMS算法可通过改变主控制滤波器步长因子以更快的方式调整滤波器的系数，从而以更好的方式增加ANC系统的收敛速度。

2.2 次级通道辅助噪声功率调度

当ANC系统采用次级通道在线建模时，辅助白噪声v(n)作为次级通道建模的训练信号充当激励。此时在误差麦克风处测得的辅助白噪声v(n)是不可消除的信号，它增加了ANC系统的残余噪声，对ANC控制滤波器的工作产生了干扰。

为了进一步提高ANC系统的性能，改进算法对次级通道辅助随机白噪声v(n)的功率进行了调整。由上文可知，参数ρ(n)可以跟踪[d(n)-y′(n)]的变化，因此可以指示ANC系统的收敛状态：ρ(0)≈1，[d(n)-y′(n)]的值变大；ρ(∞)≈0，ANC系统收敛，并且[d(n)-y′(n)]的值降低。通过文献[6]可知，当辅助白噪声v(n)的功率较大时，次级通道建模精度会更高，但同时会导致主控制滤波器更差的性能和更大的残余噪声。因此，为了权衡主控制滤波器和次级通道建模滤波器之间的相互影响，调整次级通道辅助白噪声功率，将次级通道辅助随机白噪声v(n)的功率调整如下：

(19)

3 电路仿真结果分析与比较

为比较改进算法和Eriksson、Akhtar以及Davari的算法结构在ANC系统中实现降噪的性能差异，本文对这几种算法在Mtalab中进行了仿真实验。为了更好地反映ANC系统的降噪性能和次级通道建模的收敛速率以及精度，使用如下公式定义：

(20)

(21)

表1 步长因子参数

图6是主控制滤波器步长因子的收敛变化情况，图7是建模滤波器步长因子的收敛变化情况。ANC系统初始运行阶段，由于参考噪声信号能量较高，控制滤波器选取较大的步长值，同时又由于参考信号对建模滤波器影响较大，所以建模滤波器选择小步长值。随着系统不断迭代，参考噪声信号逐渐减小，控制滤波器步长因子从大到小变化，建模滤波器步长因子则从小到大变化。从图6可以看出：当系统迭代到1 000次时，主控制滤波器步长因子基本收敛。从图7可以看出：本文提出的改进算法的步长因子有着快速收敛的速度，从而加快了次级通道建模的收敛速度，提高了建模精度。

图6 主控制滤波器步长变化

图7 次级通道建模滤波器步长变化

ANC系统的降噪性能和次级通道建模误差分别如图8、9所示。从图8可以看出：当主通道滤波器迭代到8 000次时，本文的改进算法就已达到收敛状态，此时Eriksson、Akhtar与Davari算法还未收敛。同时，在降噪性能方面，本文提出的算法也优于其他3种算法。从图9可以看出：本文提出的算法较Eriksson和Akhtar算法获得了更低的次级通道建模误差值，同时在收敛速度方面也获得了最佳效果。

图8 降噪量

图9 次级通道建模误差

本文提出的改进FxLMS算法结构和已有FxLMS算法结构具体性能参数对比如表2所示。

表2 本文与ANC现有算法的性能比较

4 结束语

本文提出了一种基于汽车风噪ANC系统次级通道在线建模的新方法。第1个改进是为噪声控制滤波器和次级通道建模滤波器的自适应算法引入最佳步长参数；第2个改进是引入次级通道辅助白噪声的自调整功率调度。仿真结果表明：与现有方法相比，该方法具有更快的收敛速度、更准确的建模精度和更好的降噪性能。 消除连续注入辅助白噪声并使用离线次级通道估计使得所提出的方法对于实际ANC系统的效果更加良好。