基于利用BP神经网络进行Stacking模型融合算法的电力非节假日负荷预测研究
李昆明 厉文婕


摘 要: 短期负荷预测尤其是非节假日负荷预测对提升电力系统整体调度、支撑电网运营工作起着十分关键的作用。目前针对非节假日负荷预测的理论、方法和应用层出不穷,但是预测精度和使用范围都受到一定限制,并且经济发展对短期负荷预测的精度提出越来越高的要求,传统的机器学习算法已经难以满足人们的需求。为了提高负荷预测的精度,本文提出了利用BP神经网络进行Stacking模型融合算法,它是基于集成学习的思想,首先挑选五种预测精度较高的单模型,然后利用Stacking模型融合方法将其集成为预测精度更高的综合模型。本文采用此算法预测某省2018年非节假日负荷,结果表明该算法可以有效提高预测精度。
关键词: 预测精度;非节假日负荷预测;BP神经网络;Stacking模型融合
中图分类号: TM 71 文献标识码: A DOI:10.3969/j.issn.1003-6970.2019.09.040
本文著录格式:李昆明,厉文婕. 基于利用BP神经网络进行Stacking模型融合算法的电力非节假日负荷预测研究[J]. 软件,2019,40(9):176-181
Research on Power Non-Holiday Load Forecasting Based on Stacking Model Fusion Algorithm Using BP Neural Network
LI Kun-ming, LI Wen-jie
(Jiangsu Fangtian Electric Technology Co., Ltd. Nanjing, Jiangsu 211102)
【Abstract】: Short-term load forecasting, especially non-holiday load forecasting, plays a key role in improving the overall dispatch of power systems and supporting grid operations. At present, theories, methods and applications for non-holiday load forecasting are endless, but the prediction accuracy and scope of use are limited, and economic development puts higher and higher requirements on the accuracy of short-term load forecasting. Traditional machine learning algorithms are difficult to meet the needs of the people. In order to improve the accuracy of load forecasting, this paper proposes a BP neural network for Stacking model fusion algorithm. It is based on the idea of integrated learning. First, select five single models with high prediction accuracy, and then integrate them by Stacking model fusion method. A comprehensive model with a higher prediction accuracy. This paper uses this algorithm to predict the non-holiday load of a province in 2018. The results show that the algorithm is effective for improving the prediction accuracy.
【Key words】: Prediction accuracy; Non-holiday load forecasting; BP neural network; Stacking model fusion
0 引言
非节假日负荷预测属于短期负荷预测,是各种类型负荷预测中至关重要的一类。负荷预测问题主要指的是对设备或系统用电功率的预测,负荷预测的准确性将会影响到电力系统的安全性、经济发展的稳定性等社会各方各面。
电力负荷预测按照预测周期分类可以被分为[1]:一是年度负荷预测,是预測负荷的年度统计量,主要包括年度最大负荷、平均负荷等关键指标量,预测时间跨度较大,也叫长期负荷预测。主要是用于解决电力系统的远景规划,解决电力系统的更新换代,以及新的线路和发电站的建设问题。二是月度负荷预测,主要预测负荷的月度统计量,主要包括月度最大负荷、平均负荷等关键指标量,也叫中期负荷预测。主要是用于解决季节性的需求问题(冬季取暖以及夏季制冷);三是日负荷预测:是预测一天内24点、48点、96点以及288点的负荷组成的负荷曲线,也叫短期负荷预测。主要是用于确定电力系统的运行方式,以保证不同发电单位的充足原料能源供应。四是时分负荷预测:通常预测的是一天内的负荷变化情况。主要是用于电力企业的电力管理系统中,解决电力系统中的实时电力调度。
本文研究短期负荷预测,主要是针对日负荷曲线的预测,在实际应用中,节假日的预测方法明显不同于一般工作日、休息日(统称为正常日,也称为非节假日),这里不做讨论。本文主要讨论的是非节假日96点的负荷曲线预测。
关于非节假日负荷预测的研究工作开展的比较早,已经有几十年的历史了。很多电力系统从业人士以及相关领域专家已经做了大量的研究工作,并且取得了不错的研究成果,有些也已经应用于实践。文献[2]采用相似日的方法进行负荷预测,取得了一定预测效果。文献[3]是基于BP神经网络及其改进算法,结合大数据平台,应用于短期负荷预测。文献[4]是利用支持向量机回归算法解决电力系统短期智能预测问题。文献[5]提出了利用专家系统法进行短期负荷预测,而时间序列模型[6,7]是被认为较经典、被广泛采用的一类短期负荷预测方法。文献[8]是在传统多元回归算法的基础上使用岭估计进行短期负荷预测。文献[9]是利用随机森林算法进行短期负荷预测研究。文献[10]利用多核函数对影响电力系统负荷波动的诸多因素进行融合,建立支持向量机预测模型,预测结果证明此种方法能够提高一点负荷预测的速度和精度。
虽然关于短期负荷预测方法层出不穷,但是目前预测模型的预测精度和使用范围都受到一定的限制。常用的机器学习的模型如BP神经网络、支持向量机、随机森林、梯度提升决策树(GBDT)、岭回归虽然有一定的预测精度,但精度难以得到進一步的提高,本文尝试融合这些模型各自的优点,对这五个模型做技术集成形成一个综合模型,理论可以证明[11],集成学习方法对于集成预测精度较高、相互独立的基模型有很好的精度提升效果,随着基模型的数量的增大,集成的错误率呈现指数级下降。集成学习的策略有多种,对于大样本(一般大于100)情况,使用学习法可以取得较高的预测精度,Stacking方法是“学习法”的典型代表。本文将使用Stacking模型融合方法进行建模,使用的初级学习器是BP神经网络、支持向量机、随机森林、梯度提升决策树(GBDT)和岭回归算法,使用的次级学习器为BP神经网络。本文将该模型应用于某省2018年电力系统非节假日负荷预测的实践中,结果发现该融合模型较各单模型预测精度得到了明显的提高,表明该模型对于提高短期负荷预测精度是有效的。
1 BP神经网络算法和Stacking模型融合方法
1.1 BP神经网络算法
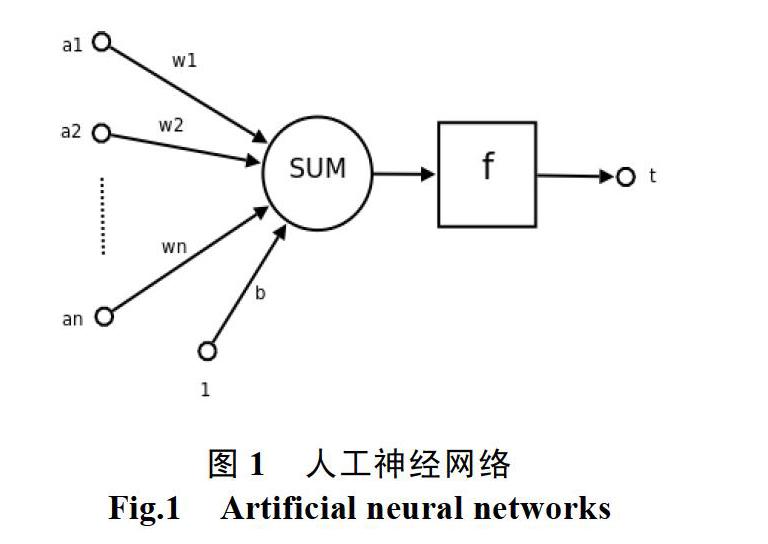
在人工智能兴起的今天,BP神经网络算法的应用越来越广泛,它是人工神经网络的极为重要的形式之一。一般意义上的人工神经网络将大脑抽象成某种根据连接形式不同而组成不同的网络模型。组成上我们可以认为神经网络是由大量的节点相互连接而成的。单个节点如图1所示。
a1,…,an为输入向量![]() 的分量,w1,…,wn为各个输入节点的权值,它们一起组成了权向量
的分量,w1,…,wn为各个输入节点的权值,它们一起组成了权向量![]() 。b称为偏置(bias),或称为阈值(threshold),f称为激活函数(activation function),通常是非线性函数。t为神经元输出,计算公式为:
。b称为偏置(bias),或称为阈值(threshold),f称为激活函数(activation function),通常是非线性函数。t为神经元输出,计算公式为:
![]()
前馈神经网络作为一种特殊的人工神经网络,主要表现在:构成前馈网络的每个神经元接收前一级的输入并将其输出到下一级而无需反馈,它可以用有向无环图表示。前馈网络通常分为不同的层,输入节点为第一层(输入层),输出节点为最后一层(输出层),中间的其他层称为隐藏层,只有输入层和输出层的前馈网络是一个二层网络,有一个隐藏层的前馈网络是三层网络,以此类推。
二层前馈网络也称为感知机,但只能解决线性问题,使用范围太窄,三层或三层以上的前馈网络的适用范围大大超过二层前馈网络,但学习较为复杂,主要困难是中间的隐藏层不直接与外界连接,无法直接计算其误差,BP算法正是为了解决这一问题才被提出来的,BP算法简而言之可以总体概括为:第一阶段是从输入层到输出层,得到每个单元的输出值;第二阶段将输出层的误差逐层向前传递,以算出各个隐藏层每个单元的误差,然后用这个误差值修正前一层的权值,称为反向传播过程。用BP算法学习的前馈网络称为BP神经网络。
BP神经网络之所以可以比较好地应用于电力负荷预测问题中,是因为其自学习能力强,并且能够拟合非常复杂的非线性函数。本文将BP神经网络用于单个模型的构建和融合模型的学习中,充分利用其优势。
1.2 stacking模型融合
Stacking模型融合方法是集成学习方法中原理简单实用性强的一类集成方法。
有监督学习算法的目标是学习出一个稳定的且在各个方面表现都较好的模型,但有时得到的却是多个有偏好的模型。集成学习的潜在想法是,即使一个弱分类器得到错误的预测,其他弱分类器也会纠正它,它是将多个弱监督模型结合起来,以获得更稳定、准确率更高的强监督模型。集成学习也称为多分类器系统。目前已经有多种集成学习模型被提出来,并且已经应用于各种类型的数据中,Stacking方法就是其中重要的一类。
集成学习的步骤可以简单概括为:先产生一系列个体学习器(个体学习器的生成),具体是个体学习器通过基学习算法训练出来;再根据需要选择不同的策略将这些个体学习器结合起来。集成学习可以分为同质和异质集成两类,其中同质集成指的是只包含同类型的个体学习器,而异质集成可以包含各种不同类型的个体学习器。如果个体学习器之间相互独立并且个体分类器拥有较高的预测准确率时,可以证明随着集成模型中个体分类器数目的增大,集成模型的错误率将会呈现指数级下降。所以如何生成并结合“好而不同”的个体学习器,是集成学习的关键。
目前的集成学习方法按照个体学习器的生成方式大致可分为两大类,一类是个体学习器之间有较强关联性需要按照次序依次生成,称为序列集成方法。另一类是参与训练的个体学习器由于有较强独立性可以并行生成,称为并行集成方法。两类方法均可以显著提高准确率。Stacking模型融合方法属于第二类方法。
关于结合策略,目前应用较多效果较好的个体学习器的结合策略有:平均法、投票法和学习法。假定集成包含T个基学习器![]() ,其中
,其中![]() 在示例
在示例![]() 上的輸出为
上的輸出为![]() ,平均法、投票法和学习法的具体结合方式为:
,平均法、投票法和学习法的具体结合方式为:
(1)平均法:主要针对的是数值型输出![]() ,此时使用平均法较为常见。平均法又分为简单平均和加权平均。
,此时使用平均法较为常见。平均法又分为简单平均和加权平均。
(2)投票法:主要针对的是分类任务,即学习器![]() 从类别标记集合
从类别标记集合![]() 中预测出一个标记,此时使用投票法较为常见。
中预测出一个标记,此时使用投票法较为常见。
(3)学习法:通过另一个学习器来进行结合,主要针对的是当训练集样本较多的情况,此时使用学习法的结合策略较为常见。Stacking模型融合方法是学习法的典型代表。在Stacking模型融合方法中,把用于结合的学习器和个体学习器分别称为次级学习器、初级学习器。Stacking模型融合方法首先训练多个不同的初级学习器,然后把之前训练的各个模型的输出作为一个新的输入来训练一个次级学习器,得到最终模型的输出。Stacking模型融合算法的具体流程如下:
输入:训练集![]() ;
;
初级学习算法![]() ;次级学习算法
;次级学习算法![]() 。
。
1: for t=1,2,…,T do
2: ![]() ;
;
3: End for
4:![]() ;
;
5: For ![]() do
do
6: For ![]() do
do
7: ![]() ;
;
8: End for
9: ![]() ;
;
10:End for
11:![]() ;
;
輸出:![]()
在训练阶段,直接使用初级学习器的训练样本来训练产生次级训练样本的过拟合风险较大,因此需要进行改进,具体实践中一般采用k折交叉验证
或者留一法来产生次级训练样本。本文以k折交叉验证为例来做简要叙述,初始训练集D被随机划分为k个大小相似的集合![]() ,令
,令![]() 和
和![]() 分别表示第j折的测试集和训练集。给定T个初级学习算法,初级学习器
分别表示第j折的测试集和训练集。给定T个初级学习算法,初级学习器![]() 通过在
通过在![]() 上使用第t个学习算法而得。对
上使用第t个学习算法而得。对![]() 中每个样本
中每个样本![]() ,令
,令![]() ,则由
,则由![]() 所产生的次级训练样例的示例部分为
所产生的次级训练样例的示例部分为![]() ,标记部分为
,标记部分为![]() 。于是,在整个交叉验证过程结束后,从这T个初级学习器产生的次级训练集是
。于是,在整个交叉验证过程结束后,从这T个初级学习器产生的次级训练集是![]() ,然后
,然后![]() 将用于训练次级学习器。图4是Stacking方法的示意图。
将用于训练次级学习器。图4是Stacking方法的示意图。
由于非节假日负荷具有明显的季节周期性变化趋势,本文将对预测模型关于不同季节分别进行建模。本文对一天中每一个预测点分别建立预测模型,以降低问题求解的规模。
选用预测基准点前一个月的负荷数据以及其他相关数据(包括气候因素数据)形成训练样本。每个输入样本的特征值包括:第一同类型日负荷、气象特征、周期特征;第一同类型日前一天负荷、气象特征、周期特征;第二同类型日负荷、气象特征、周期特征;第二同类型日前两天负荷、气象特征、周期特征;待预测日的气象特征、周期特征。输出为待预测日的负荷。
由于特性指标的量钢和数量级都各不相同,本文在建模之前需要进行数据规范化处理,解决数据指标之间的可比性问题。具体需要做以下的不同 处理:
(1)负荷数据的归一化
本文采用归一化公式:
其中,![]() 为未处理的原始样本数据,
为未处理的原始样本数据,![]() ,
,![]() 分别为
分别为![]() 中的最大值、最小值,
中的最大值、最小值,![]() 为归一化后的数据。
为归一化后的数据。
(2)日类型特征的划分与规格化
由于日类型特征数据是标签型数据,不方便用于预测模型中,本文将用数字来代替不同日期类型,根据非节假日负荷的周期性特点,可以将周一取为0.8,将周二到周五取为0.9,将周六取为0.5,将周日取为0.4。
(3)温度数据的规格化
采用如下函数规格化:![]()
式中,![]() 代表溫度℃,
代表溫度℃,![]() 规范化后的特征。
规范化后的特征。
(4)天气类型
由于天气类型特征数据是标签型数据,不利于建模,本文将天气类型转化为[0,1]之间的值。
2.3 非节假日负荷预测建模
为了建立非节假日负荷的预测模型,本文将使用利用BP神经网络进行Stacking模型融合的方法,使用的初级学习器有:BP神经网络算法、随机森 林算法、GBDT算法、支持向量机算法、岭回归算法,使用的次级学习器为:BP神经网络算法。具体做法是:
(1)首先将处理好的训练集数据划分为训练集和验证集,划分比例为4∶1,待预测点的特征数据集为测试集。
(2)对训练集数据采用5折交叉验证方式对每一个初级学习器进行训练,得到的预测值组成5维的新特征向量,与原本的负荷实际值组成新的训练集。同时得到验证集的新特征向量和负荷实际值组成新的训练集,得到测试集的新特征向量形成新的测试集。
(3)对新的训练集,用次级学习器BP神经网络算法进行训练,得到Stacking融合模型,对新的验证集进行验证,对新的测试集进行预测。
2.4性能评估
短期负荷预测模型的性能通过平均绝对误差比率来进行评估:
![]()
其中,![]() 为负荷的实际值,
为负荷的实际值,![]() 为负荷的预测值,T为负荷采样的总数。
为负荷的预测值,T为负荷采样的总数。
3 算例分析
为了验证stacking模型融合算法应用于非节假日负荷预测的有效性,本文采用某省2018年历史统调负荷数据,对原始数据进行数据清洗、数据规范化等特征处理后,得到训练数据集、验证数据集和测试数据集,对stacking融合模型进行训练,得到训练好的模型,下面是初级模型和融合模型的结果评估表。
结果表明:当样本量较大时,Stacking融合模型的性能较单个模型有明显的提升。并且本文中对负荷预测做了一段时间的跟踪,得到了测试集的真实负荷,通过误差计算,得到各单模型的准确率为:93.75%、94.21%、94.58%、93.72%、92.91%,而Stacking融合模型的准确率为:96.18%,准确率得到了显著提高,再次验证了Stacking融合模型的性能优于各初级学习器的性能。因此,本文选择stacking融合模型算法预测非节假日负荷是有效的,经过实践检验是有应用价值的。
4 结论
本文提出了一种非节假日短期负荷预测建模的新思路,传统单模型负荷预测方法实际上已经十分成熟,一批常见的机器学习算法如BP神经网络算法、支持向量机、GBDT算法、随机森林算法、岭回归算法在实践应用中得到了较好的预测效果,为了在此基础上进一步提升算法的性能,需要结合各个单模型算法的优点,对“好而不同”的单模型进行集成,Stacking模型融合通过学习的方式对选取出的五个优良的单模型进行融合,通过实际案例验证,证明了其能够显著提高单模型的性能,具有十分突出的应用价值。
参考文献
- 康重庆, 夏清, 刘梅. 电力系统负荷预测[M]. 北京: 中国电力出版社, 2007.
- 李滨, 黄佳, 吴茵, 等. 基于分形特性修正气象相似日的节假日短期负荷预测方法[J]. 电网技术, 2017, 41(6): 1949-1955.
- 苏学能, 刘天琪, 曹鸿谦, 等. 基于Hadoop架构的多重分布式BP神经网络的短期负荷预测方法[J]. 中国电机工程学报, 2017, 37(17): 4966-4973, 5216.
- 唐杰明, 刘俊勇, 杨可, 等. 基于灰色模型和最小二乘支持向量机的电力短期负荷组合预测[J]. 电网技术, 2009, 33(3): 63-68.
- Ho Ku-Long, Hsu Yuan-Yih, Lee C E, et al. Short-term load forcasting of Tai-wan power system using a knowledge-based expert system[J]. IEEE PWRS, 1990, 5(4): 46-57.
- 刘晨晖(Liu Chenhui). 电力系统负荷预报理论与方法(Theory and Methodology of Power System Load Forecasting). 哈尔滨: 哈尔滨工业大学出版社(Harbin: Press of Harbin Institute of Technology). 1987.
- 牛东晓, 曹树华. 赵磊, 等. (Niu Dongxiao, Cao Shuhua, Zhao Lei, et al). 电力负荷预测技术及其应用(Power Load Forecasting Technology and Its Application). 北京: 中国电力出版社(Beijing: China Electric Power Press). 1998.
- 陈慧玉, 孟宪生. 岭估计在上海居民生活用电预测中的应用(The Practice of Ridge-estimation in the Forecast of Shanghai Residents' Domestic Electricity Consumption). 高效應用数学学报(A辑)(Applied Mathematics A-Journal of Chinese University), 1998, 13(4): 421-426.
- 高亚静, 孙永健, 等. 基于新型人体舒适度的气象敏感负荷短期预测研究[J]. 中国电机工程学报, 2017.
- 吴倩红, 高军, 侯广松, 等. 实现影响因素多源异构融合的短期负荷预测支持向量机算法[J]. 电力系统自动化, 2016, 40(15): 67-72, 92.
- 周志华. 机器学习[M]. 北京: 清华大学出版社, 2016, 172-173.

