对决定标枪最优飞行距离相关因素的探析

苗成双　熊悦希　付可馨　胡兰月

【摘 要】本文主要研究的是针对标枪的投掷运动中，不同因素对标枪投掷距离的远近产生不同程度的影响。首先固定参数，建立线性回归模型，得到标枪的最佳出手速度、出手角、初始攻角等。然后建立二阶常微分模型，求得标枪的最优飞行远度。最后，将各因素分类，进行灵敏度分析，得到各因素对标枪投掷距离影响的相对重要性排序，从大到小依次为：出手速度、出手角、风速、初始俯仰角、攻角。

【关键词】二阶常微分模型;Matlab;掷标枪的距离;线性回归模型;SPSS

中图分类号： O175.8 文献标识码： A文章编号： 2095-2457（2019）30-0013-003

DOI：10.19694/j.cnki.issn2095-2457.2019.30.006

0 引言

掷标枪是一项古老的田径运动。标枪投掷距离的远近与众多因素有关，比如与标枪的技术参数（标枪的长度、重量、重心的位置、几何形状、形心的位置等）有关，与运动员水平（出手的速度、出手高度、出手角、初始攻角、出手时标枪的初始俯仰角速度等）有关，与比赛环境（风力、风向、空气的密度与粘度等）有关。

1 参数的选取

设标枪为刚体，枪身由铝合金制成，其密度为2.7×103kg/m3，枪头由合金钢制成，其密度为7.8×103kg/m3。标枪的几何尺寸采用文献【国家标准】 GBT 22765-2008-标枪中数据。为便于讨论，假设运动员出手高度为，标枪重量为且不考虑标枪在飞行过程中的进动影响。空气密度为1.184×10-3g/cm3，空气粘度为1.84×10-15pa·s（帕·秒），进行问题探究。

2 模型建立

2.1 标枪的投掷距离的模型建立

易知投掷标枪的运动轨迹是一条抛物线，如下图抛物线所示：

图1 标枪投掷轨迹图

由上图建立模型[1]：

L=■[v■tanθ+■]

2.2 标枪的运动轨迹模型建立

2.2.1 只考虑空气阻力作用

我们考虑空气阻力作用时标枪的运动轨迹和受力情况，将标枪所受到的空气阻力分解为水平方向和竖直方向的两个分力，即标枪在水平和竖直方向的两个运动方程为：

m■=-fcosθm■=-fsinθ-mgf=6πηrV■

同时，我们已知两组四个初始条件：

（1）t=0时，x=0，■=V■cosθ

（2）t=0时，x=0，■=V■sinθ

通过常微分方程的求解，我们可以得到空气阻力作用下标枪的运动方程[3]（考虑空气阻力时标枪作斜抛运动位置参数方程）为：

x=■（1-e■）y=（■+■）（1-e■）-■t

联立上式，消去时间参数t即可得出标枪在受到空气阻力时的运动轨迹方程：

y=tanθ+■x+■ln（1-■x）

2.2.2 考虑空气阻力和风速同时作用

考虑空气阻力和风速同时作用时的斜抛运动方程。需要通过对标枪的受力进行分析，列出微分方程。设风速为Va。对物体受力分析后可列出二阶常微分方程[4]：

-kV■=ma■-kV■=ma■

其中，V■=■，a■=■V■=■，a■=■

联立解得如下，标枪在受到空气阻力和风速同时作用时的运动轨迹方程：

x=■mcosθ-■me■cosθ

y=（■+mg+V■ksinθ/k■）me■+（-V■-■）t+■m

2.4 各要素对标枪投掷距离影响模型建立

在掷标枪运动中，根据标枪飞行的实际情况，标枪的飞行远度应取决于三个方面的因素。按各因素的重要程度排列其顺序，它们分别是标枪飞行的初始条件、标枪的参数和天气因素。

因此，要想判断运动员出手速度、出手角、初始攻角、初始俯仰角速度、风向及风速等要素对标枪投掷距离影响的相对重要性，需要对影响因素进行灵敏度分析。模型建立如下：

σi=100%×■，（i=1，2，3，4）

其中，Δx■表示第i个因素变化而使得投掷距离变化，x表示原始投掷距离，σi表示第i个因素对投掷距离产生变化的变化率。

3 模型求解

3.1 投擲距离最大

要求当投掷出手速度为30m/s时，对附表中24名运动员数据的分析选取出最佳出手角度区间为[35°，40°]，最佳的攻角为[-10°，5°]，在区间内以0.3°为步长，运用迭代的思想编写程序。流程图如下所示：

图2 最大投掷距离求解流程图

运行程序之后得到如下数据（部分）：

表1 以0.3为步长迭代数据

最终得出手角42.7°，攻角为-3.3°时，投掷距离最大，最大投掷距离为：86.49m。

3.2 标枪的投掷距离的模型求解

所以，当运动员投掷出手速度为31.70m/s，风向分别为顺风和逆风，风速分别为3m/s、6m/s、9m/s时，我们采取同3.1的解决方案。最佳出手角度区间为[35°，40°]，最佳的攻角为[-7°，3°]，最佳初始俯仰角区间为[-5°，5°]，在区间内以0.3°为步长，运用迭代的思想编写程序，运行程序得到在每个出手角、攻角、俯仰角下的投掷距离。并分情况讨论顺风和逆风环境，得到如表2。

3.3 各要素对标枪投掷距离影响模型求解

3.3.1 出手角的灵敏度分析

由于本文上述模型可以求解出若干组以0.3为步长进行遍历的数据集，所以再次利用模型求解出20组特定数据，再利用控制变量法求解出因变量“投掷距离x”的变化量或变化率即可完成对因素灵敏度的分析。将数据带入模型中，求解出一组结果，如表3。

表3 出手角对投掷距离的影响的初始数据

根据上表数据，固定出手速度、风速、攻角、俯仰角的值不变，以5%的变化量改变出手角的值，带入模型求解出不同的投掷距离，进而求得变化率。计算结果如表4（部分）。

表4 出手角对投掷距离影响及变化率

由表可知，变化率与出手角的成正比，投掷距离与俯仰角则成反比。出手角使得投掷距离变化的变化率为：

σ1=100%×■=■×100%=0.0077

3.3.2 出手速度的灵敏度分析

同上可得：

表5 出手速度对投掷距离影响及变化率

由表可知，变化率与出手速度的成反比，投掷距离与出手速度则成反比。出手速度使得投掷距离变化的变化率为：

σ2=100%×■=■×100%=0.0762

3.3.3 初始俯仰角的灵敏度分析

同上可得：

表6 初始俯仰角对投掷距离影响及变化率

由表可知，初始俯仰角与变化率成正比，俯仰角与投掷距离则成反比。初始俯仰角使得投掷距离变化的变化率为：

σ3=100%×■

=■×100%=-0.00029

3.3.4 风速的灵敏度分析

同上可得：

表7 风速对投掷距离影响及变化率

由表可知，风速与变化率成反比，俯仰角与投掷距离则成正比。风速使得投掷距离变化的变化率为：

σ4=100%×■=■×100%=0.0051

3.3.5 攻角的灵敏度分析

同上可得：

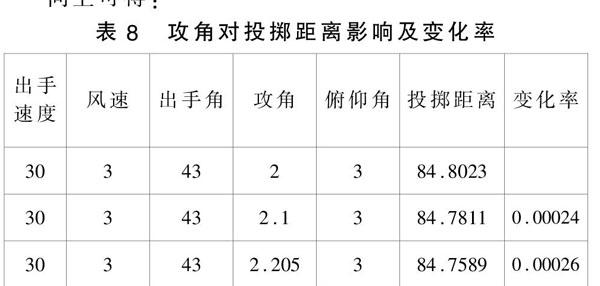
表8 攻角对投掷距离影响及变化率

由表可知，攻角与变化率成反比，攻角与投掷距离则成反比。攻角使得投掷距离变化的变化率为：

σ5=100%×■=■×100%=0.00025

结果分析：

表9 输出结果

因此，各因素对标枪投掷距离影响的重要性从大到小依次为：出手速度、出手角、风速、初始俯仰角、攻角。

4 结语

本文中的模型不仅可以用于标枪投掷問题，还可以推广到其他运动中。此外，还可以根据此来引导运动员的一些运动习惯，从而在训练和比赛中队运动员和教练有一定的理论指导意义。

【参考文献】

[1]琚鑫，岳凌月，王邦平.斜抛运动中射程问题的一般性讨论与数值计算[J].物理通报，2013（6）：118-120.

[2]张健.考虑空气阻力和风速影响的斜抛运动的数值分析[J].科技风，2017（14）.

[3]郭雪鹏.考虑空气阻力的斜抛运动研究[J].物理教学，2017，39（04）：14-16.

[4]唐伟跃，陈铁生，陈香才， et al.斜抛运动方程的分析[J]. 河南教育学院学报（自然科学版），2005，14（2）：27-28.