适应性市场假说的实证研究
——基于国际现货贵金属市场*
杨胜刚,彭啸帆,邹子昂,熊军凯
(湖南大学 金融与统计学院,湖南 长沙 410079)
1.引言
以金银、铂金和钯金为代表的贵金属有着广泛的用途,如制成珠宝、用于电子设备的生产等等。同时,这类贵金属也具有价值储藏的职能,从而被人们当作财富持有。历史上,黄金和白银最初由于其稀有性、可分割性以及不易磨损性而充当货币的角色,铂金和钯金则直到近些年来才被列入到贵金属的名单当中,最初是被视为一种工业商品。如今,越来越多的个人投资者或金融机构将这些贵金属看作一种可用于投资的资产,发生这种转变的主要原因在于:主要贵金属与股票、债券等证券的收益不存在相关关系,因此这些贵金属能够给传统的证券投资组合带来显著的多样化收益,从而规避证券市场上的风险。加上ETF的出现,又进一步刺激了投资者对贵金属的需求,因此,贵金属逐渐成为一种富有吸引力和十分重要的投资品[1]186-205,[2]。
当前,主要贵金属在资产组合选择和管理当中已经占有相当重要的地位,投资者会根据这些贵金属的价格作出买卖决策,因此这些贵金属的定价效率问题受到了极大的关注。在金融领域,Fama(1970)[3]383-417提出的有效市场假说(EMH)是论述资产价格行为特征最为重要的理论之一。EMH认为,如果一个市场是有效市场,那么该市场上的价格总是充分反映了基于当前时刻可得到的信息集中的内容,价格呈随机游走时现象。因此,市场上不存在任何获取超额收益的机会。EMH将市场有效性划分为三个层次形式:弱式有效市场、半强式有效市场和强式有效市场,如果弱式有效市场成立,那么任何主动投资策略都不可能获得超额利润;如果半强式有效市场成立,则基本面分析策略也将失效;如果强式有效市场成立,那么即使是内幕消息也无法带来超额回报。此后,许多学者对EMH作了理论与实证上的检验,发现市场存在诸多与EMH理论相矛盾的现象,例如规模效应、价值效应等。基于这一现象,行为经济学家对EMH理论中投资者理性的基本假设提出质疑。行为金融理论认为投资者是非理性的,在决策时会受到各种偏差的影响[4]307-343,[5]1839-1885,因此价格并不是随机游走的,而是会经常同方向变动,市场在一般情况下是无效的。
关于有效市场假说的争论不断出现,为了调和EMH与行为金融理论之间的分歧,Lo (2004)[6]15-29从发展的角度出发,提出了适应性市场假说(AMH)。AMH理论起源于进化论和有限理性理论。有限理性理论认为,市场参与者搜集或者处理信息的能力有限,加上进行最优化决策本身具有一定的成本,因此有限理性的市场参与者往往不会以最优化作为决策目标,而是以令他们满意的结果为目标进行决策来作为对最优化决策的替代[7]99-118。AMH理论根据进化论的观点对有限理性理论进行了改进,认为市场上的个体依据试错法而非分析判断来确定令他们满意的目标。在经济政治环境稳定的情况下,由这一方法所作出的决策会逐渐接近最优化决策。一旦环境发生改变,在旧环境下的试探方法会因为不适应新环境而使得市场参与者产生行为偏差。如同自然界一样,市场上的自然选择法则会使得适者生存,并由此决定新环境中市场参与者的数目以及构成。市场参与者会不断地适应环境,并根据试错法来作出决策。AMH理论认为,投资策略的获利能力会根据经济环境的变化、进入和退出的行业竞争者数量以及获利机会的类型等因素而历经周期性变化,金融市场的有效性也就呈现出一种周期变化的现象。Lo(2005)[8]21-44将AMH理论的主要内容概括为:(1)市场上的个体根据自身利益采取行动;(2)市场上的个体会犯错;(3)市场上的个体会学习和适应环境;(4)竞争促使适应和创新;(5)自然选择塑造市场生态;(6)进化决定市场动态。
总的来说,根据AMH理论的观点,有效市场假说是市场这一生态系统的极限行为,而行为偏差则是特定物种在一定条件下的行为,这种行为可能是持续的也有可能是非持续的,依赖于一定的经济演化路径[9]25-26。
市场有效性对于说明市场信息传播的速度、价格的可预测性以及市场上是否存在盈利机会有着重大的意义,有效市场成立与否对投资者投资策略的选择至关重要。AMH理论对市场有效性动态变化的规律及其原因提供了解释,从而得到学者、投资者和政策制定者的极大重视,加上贵金属市场在金融市场中的地位日益上升,因此有必要研究贵金属市场的时变有效性。在这一背景下,本文基于time-varing AR模型对贵金属现货市场的时变有效性进行实证分析,探讨AMH理论的观点是否能够在国际贵金属现货市场当中成立,并对市场有效性的演变特征及其影响因素进行分析,从而为政策制定者、投资者以及贵金属领域的研究者提供一定的参考。
2.文献综述
目前国外文献关于贵金属市场适应性有效的研究较少,研究的主要对象仍然是黄金和白银市场的有效性。国外对黄金市场有效性的研究最早可以追溯到Tschoegl (1980)[10]371-379,他是第一个在黄金市场上对弱式有效市场假说进行实证检验的人。Tschoegl发现,在交易成本能够被测算出来的情况下,即使黄金价格存在序列相关,交易策略依然无法获得超额利润。Solt & Swanson (1981)[11]453-478以及Koutsoyiannis (1983)[12]563-581先后发现亨特兄弟对黄金市场的垄断会导致黄金价格序列的自相关性。Cheung & Lai (1993)[13]181-202研究发现1970年代初至1980年代末的黄金收益率呈现出长记忆性。进一步的实证结果表明,出现这一现象的主要原因在于其数据与中东政治局势高度紧张的时期具有相关性,并且受到了当时亨特兄弟垄断市场的影响。Ivanova & Ausloos (1999)[14]665-669以及 Byers & Peel (2001)[15]253-260利用其他的模型,也得出了同样的结论。Charles et al.(2015)[16]284-291以及 Ntim et al.(2015)[17]218-236都对黄金市场的时变有效性进行了研究。Charles et al.发现,主要贵金属的市场有效性程度会随着时间的推移而逐渐增强。而Ntim et al.则指出,在新兴市场,黄金价格序列具有一定的可预测性。并且,这种可预测性会随着时间的变化而发生改变。在有关白银市场有效性的研究方面,前面所提及的Solt & Swanson (1981)是最早对白银市场有效性进行研究的文献之一。他们发现,白银价格具有序列相关性以及异方差性,虽然这不足以说明市场上存在获得超额收益的机会,但是他们相信白银市场是一个比一般投资市场更具有投机性的市场。Aggarwal & Sundararaghavan (1987)[18]49-64则利用马尔科夫链模型检验了白银期货市场的有效性。实证结果表明,亨特兄弟对白银期货市场的人为操纵造成了市场的非有效性。Frank & Stengos (1989)[19]553-567对白银收益率的可预测性进行了考察,发现在样本期间内,白银收益观测值的产生过程是一个非线性过程,表明白银价格是一个不可预测的随机变量。Charles et al.(2015)则在白银和铂金现货市场上进行了同样的研究。结果表明,这两个市场均符合适应性有效市场假说(AMH)的观点,并且这两个市场的有效性在样本期间内都出现了逐渐增强的趋势。
国内学者还没有对贵金属市场的时变有效性进行过探讨,研究的焦点依然在贵金属市场的静态有效性上,如于虎山和秦学志(2009)[20]19-22、秦俊琦和邹楚楠(2009)[21]140-141以及张露露(2010)[22]55-56都对上海黄金期货市场的有效性进行了实证检验。于虎山和秦学志(2009)以及张露露(2010)先后使用协整检验、误差修正模型以及格兰杰因果检验等方法对上海黄金期货市场进行有效性检验,而秦俊琦和邹楚楠(2009)则使用游程检验、Johansen协整检验等方法对上海黄金期货市场的有效性进行检验,上述学者所得出的结论均为上海黄金期货市场还未达到弱式有效。谢家敏(2009)[23]89-91则对中美黄金期货市场的有效性进行了对比分析,发现黄金期货市场中存在非有效因素,而且黄金现货价格单向引导黄金期货价格,美国现货价格信息对期货价格的作用高于中国水平。近年些来,也有一些学者开始对国际现货贵金属市场的有效性进行了研究。杨世伟、吴青(2013)[24]37-46基于方差比率检验法,对国际现货贵金属市场进行了有效性检验,结果表明国际现货贵金属市场尚未达到弱式有效。
综合前人的研究经验,本文的主要贡献在于:第一,将钯金市场和铂金市场纳入研究范围之内,能够对国际现货贵金市场的整体特征有更加准确的认识。第二,目前国内有关贵金属市场有效性的研究当中还没有涉及到适应性有效。市场适应性有效是一种比传统市场有效要弱的有效形式, 市场要达到有效, 首先应适应性有效[25]76-80。因此,本文对适应性有效的研究可以推动贵金属市场有效性的研究发展。第三,方法上的改善。TV-AR模型可以提供一个更加精确量化时变有效性的指标,并且避免了滑动窗口方法最优窗口宽度上的经验选择问题。第四,对四个贵金属市场之间的有效性进行了比较分析,从而考察各贵金属市场在金融市场中的地位。
3.研究设计
3.1样本选取
伦敦金属交易所(LME)成立于1876年,是全球最大的有色金属交易所,因此,伦敦金属交易所的价格和库存对世界范围内的有色金属生产和销售都有着重要的影响。本文选取1987年3月至2016年12月伦敦金属交易所的黄金、白银、铂金、钯金的周数据作为研究样本,时间跨度为30年,总共获得了5217笔数据。数据来源于wind数据库。
我们定义稀有贵金属的收益率如式3.1
(3.1)
Pt表示的是t时刻稀有贵金属的收盘价,Pt-1表示的是t-1时刻稀有贵金属的收盘价,Rt表示的是t时刻稀有贵金属的收益率。
3.2模型方法
3.2.1 EMH与长期乘数
EMH的观点在数学上可以表示为如下形式:
(3.2)

假设{xt}是平稳的时间序列,按照wold分解,可以把xt的时间序列过程分解为如下形式:
xt=φ(L)ut
(3.3)

3.2.2非贝叶斯TV-AR模型
本文参考Mikio Ito(2016)建立的非贝叶斯TV-AR估计模型。在金融学当中,AR(q)模型常常被用来进行金融资产收益率的时间序列分析,其形式如下:
xt=α0+α1xt-1+…+αqxt-q+ut
(3.4)
其中,xt代表贵金属在t时刻的收益率;{ut}是一个白噪声序列,其满足E[ut]=0, E[u2t]=σ2,以及对所有的m≠0,E[utut-m]=0。与一般的时间序列分析中假定αq为常数不同,TV-AR模型认为AR模型中的系数是时变的,并将其应用于实际金融市场当中,用于表示贵金属市场结构的变化。
经调整后的模型总体空间形式如下:
(3.5)
(3.6)
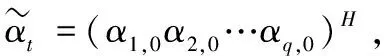
X=Zβ+u
(3.7)
γ=wβ+v
(3.8)
其中:



(3.9)
最后使用最小二乘法(OLS)或者是广义最小二乘法(GLS)来估计非贝叶斯TV-AR系数(2)这里能使用OLS和GLS的原因具体可参照Mikio Ito(2016)中的注脚11。。
3.2.3 时变市场有效性的程度衡量
接下来利用非贝叶斯TV-AR模型来进行系数估计。首先要估计出TV-AR(q)模型中的系数,为了确定AR(q)中适当的滞后阶数,我们选择采用施瓦茨贝叶斯信息准则(Schwartz Bayesian Information Criterion,SBIC)。确定滞后阶数q之后,我们按照前述方法估计出TV-AR模型当中的系数。第二步,从非贝叶斯TV-AR(q)模型中可以得到TV-MA(∞)模型,形式如下:
xt=ut+φ1,tut-1+φ2,tut-2+…
(3.10)
根据Lütkepohl(2005)[27]88-89,TV-MA(∞)模型的参数估计值可以根据TV-AR(q)中参数估计值,按照以下公式得出:
而与时变系数有关的时变长期乘数则可以根据下式计算得出:
根据(Mikio Ito,2016)的思想,这一时变长期乘数衡量了市场与有效市场的偏离程度,当市场有效时,φ1=φ2=…=0,α1=α2=…=αq=0,此时,长期乘数φ=1;反之,φ将会偏离1。因此,φ可以被称为市场有效性程度。
最后,Akihiko Noda(2016)[28]66-71对前面的长期乘数进行了变换重新构建了一个时变有效性程度指标,用下式进行计算得出:
(3.11)
其中ζt衡量了对应于TV-AR(q)模型的TV-MA(∞)模型中的系数与0的偏离程度,由前面所述可知,TV-MA(∞)模型中的系数与0偏离越远,市场有效性就越弱。因此,若ζt远远偏离0,则意味着市场存在低效率。
4.实证检验与结果分析
4.1描述性统计
图1和表1分别给出了四个贵金属现货价格的时序图和四个贵金属收益率序列的统计特征。

从图1中可以明显看出,贵金属的价格水平整体呈上升趋势,但是在几个时期内出现过明显的剧烈波动:铂金和钯金的价格在20世纪末出现了剧烈的波动,尤其是钯金的价格波动幅度非常大;而在2008年前后,四个贵金属现货价格都在迅速上涨,在2011年前后也出现了同样的现象。由后面的分析可知,这些贵金属价格的剧烈波动都与重大经济政治事件的冲击有关系。

表1 伦敦交易所稀有贵金属收益率的统计特征
表1给出了收益率的描述性统计量,由表1可知,铂金、钯金、白银和黄金的平均收益率分别为0.000399、0.00117、0.000752和0.000731,很显然,铂金的平均收益率要远小于其他三种稀有贵金属,而黄金和白银的平均收益率比较接近,钯金的平均收益率最高。从标准差来看,四种稀有金属中,黄金的风险最小,而钯金的风险最大,铂金与白银的风险程度相近。另外,白色贵金属收益率的偏度均小于0,黄金收益率的偏度则大于0,说明白色贵金属的收益率在统计分布上均呈负偏态,而黄金收益率则呈正偏态。并且,这四种稀有贵金属收益率的峰度都要远大于3,因而均表现出尖峰厚尾的特征。
4.2平稳性检验
如果时间序列不存在单位根,则说明该序列平稳,反之则序列不平稳。为了检验序列是否平稳,选用ADF-GLS检验方法,通过Stata11.0软件对稀有贵金属的收益率序列进行检验,检验结果如表2所示。

表2 平稳性检验结果
由表2可知,黄金、白银、铂金和钯金的ADF-GLS统计量分别为-4.443、-24.705、-3.626和-24.734,很显然都要小于置信水平为1%时的临界值。这说明,ADF-GLS检验拒绝了原假设,因此各序列不存在单位根,即各序列都为平稳序列。
4.3实证结果分析
4.3.1静态检验及初步估计
首先,我们根据SBIC准则来确定一个标准的AR(q)模型(即参数为常数的AR(q)模型)的最优滞后阶数。结果显示,AR(q)模型在四个贵金属现货市场上的最优滞后阶数都是1,因此,我们选择一阶自回归模型(AR(1))。表3给出了全样本AR(1)模型的回归结果。

表3 AR(1)模型估计结果
根据表3的结果可知,黄金、白银、铂金和钯金的p值分别为0.724,0.741,0.642和0.285。这表明,在四个贵金属现货市场中,AR(1)模型的参数在1%、5%和10%的显著性水平下均无法通过t检验,即无法拒绝参数为0的原假设,四个贵金属现价收益率序列均不存在序列相关性。因此,四个贵金属现货价格收益率序列呈现出随机游走的现象,EMH假说通过检验。接下来,为了验证AMH假说是否成立,我们将根据基于TV-AR模型构建的有效性程度指标对四个贵金属现货市场有效性的动态变化进行探究。
4.3.2国际现货贵金属市场的时变有效性
图2是基于TV-AR(1)模型所得出来的四种稀有贵金属现货市场有效性程度指标的时序图。从图中我们可以看到,黄金、白银、铂金和钯金的市场有效性都是随着时间的变化而不断改变的,因此表明有效性是一个时变的概念。并且,可以直观地看出,在四个市场当中,黄金市场有效性程度指标的波动幅度相对最小,而钯金市场的波动幅度则相对最大,这四个市场的有效性特征我们会在后面再进行详细分析。

由图2可知,黄金市场的有效性程度指标的波动范围处于0~0.1的区间内。其中,在1999年、2001年以及2007—2008年期间,黄金市场的有效性程度指标均出现了波峰,这与1997年亚洲金融危机、2001年“9·11”恐怖袭击事件以及2008年次贷危机相对应,反映出两次全球金融危机和政治相关事件的爆发对黄金市场的冲击,使得黄金市场的有效性被削弱。值得注意的是,黄金市场在背离有效市场之后,市场有效性会随着时间的推移逐渐增强,如果不受其他因素冲击的话,市场就会逐步回复到有效市场。
由图2可知,白银市场的有效性程度指标的波动范围处于0~0.17的区间内。其中,在1997年以后,白银市场的有效性程度指标有小幅度的上升,这与亚洲金融危机的爆发相对应,说明金融危机的爆发使得白银市场上的投资者变得非理性,从而减弱了市场有效性。此后,白银市场的有效性再次增强,说明投资者由非理性逐渐转向理性。同样,在2004年、2007年以及2011年,由于几次全球性或区域性金融危机的爆发以及利比亚战争的爆发,使得白银市场的有效性下降,但是在之后几年里白银市场的有效性又逐渐增强。
由图2可知,铂金市场的有效性程度指标的波动范围在0~0.24的区间内。其中,有效性程度指标在2001年出现过波峰,在2008—2009年期间达到最大,接近0.25,说明在这两个时期,铂金市场的有效性最弱,并且自2011年之后,市场有效性有变弱的趋势。这一结果与2001年“9·11”恐怖袭击事件、2008年美国次贷危机所引发的全球金融危机以及2011年利比亚战争的爆发相对应。说明政治事件和次贷危机的爆发对市场投资者心理产生了影响,从而使得铂金市场的有效性减弱。此外,与黄金和白银市场相似,铂金市场在遭受冲击导致有效性减弱之后,经过一段时间也会逐渐回复到有效市场。
由图2可知,钯金市场的有效性程度指标的波动范围处于0~0.5的范围内。钯金市场有效性程度指标的波峰出现在2001年、2004年、2008年和2011年,说明在这四个时期钯金市场几乎是无效的。这基本上与2001年“9·11”恐怖袭击事件、2008年美国次贷危机以及2011年利比亚战争相对应,可以看出,在经济危机和政治局势紧张的背景下,经济政治环境的变化会使市场参与者趋向非理性,这种投资者的非理性使得钯金市场的价格无法真实地反映市场上的信息,因此,钯金市场在这些时期会偏离有效市场。最后,与前面三个市场相同,钯金市场因经济政治环境变化的冲击而偏离有效市场状态之后,具有向有效市场回复的趋势。
根据实证结果可以发现,四个贵金属市场的有效性发生波动从而偏离有效市场的时期主要集中在以下几个时段:
一是1997年前后,这一时期亚洲金融危机的爆发使得黄金和白银市场的有效性都有一定程度的削弱,从而使得这两个市场都偏离了有效市场。
二是2001年前后,“9·11”恐怖袭击事件的爆发不仅对美国民众造成了极为深远的心理影响,并且也对全球经济产生了重大影响,全球经济也因该事件受到了较为严重的打击。四个现货贵金属市场的有效性程度指标均在这一时期出现了波峰,即四个现货贵金属市场都偏离了有效市场。
三是2007—2008年,美国次贷危机的爆发引发波及全球的金融危机,由于贵金属资产的避险特性,投资者将资金投入贵金属市场以规避风险,从而引发黄金、白银、铂金和钯金价格的迅速上升。由图2可以看出,四个贵金属现货市场的有效性程度指标在2008年前后均有不同幅度的上升,说明四个贵金属市场均受到了金融危机的冲击。
四是2011年之后,利比亚战争的爆发使得四个现货贵金属市场的有效性都出现了不同程度的削弱,尤其是白银市场和钯金市场受到了比较严重的冲击。另外,朝鲜核危机问题也对全球政治环境产生了深远的影响,使得现货贵金属市场受到了一定的冲击,从而偏离有效市场。
综上所述,现货贵金属市场偏离有效市场的时期与经济危机爆发以及政治局势紧张的时期基本相吻合,由此我们推测,经济政治环境的变化可能会对现货贵金属市场造成冲击,使得其偏离有效市场,这也印证了AMH关于市场有效性与环境高度相关的预测。按照这一观点,市场弱式有效的检验结果可能会因为样本的不同而产生偏差,这意味着对市场效率的研究应该要从动态的角度出发,考察不同时段的市场有效性。同时,定价效率也会随着市场环境的变化而改变,投资者应该采取动态的投资策略。
4.3.3国际现货贵金属市场间有效性比较
除了对单个现货贵金属市场有效性进行静态和动态分析之外,我们还对四个贵金属现货市场之间的有效性进行了对比分析,分析结果如表4所示。

表4 贵金属现货市场有效性程度指标的统计特征
表4给出了四个贵金属现货市场有效性程度指标的统计特征。其中,黄金市场有效性程度指标的均值最小,大约只有排名第二的白银的三分之一。表明从整个样本时期来看,四个贵金属市场中黄金市场的有效性相对最强;而钯金市场有效性程度指标的均值最大,说明样本期间钯金市场有效性相对最弱。从方差和标准差上来看,四个市场中,黄金市场的标准差和方差最小,而钯金市场的标准差和方差最大,因此说明黄金市场有效性程度相对波动最小,而钯金市场相对波动最大。
结合Charles et al.(2015)的结论,出现这一现象的原因可能在于:第一,在四个贵金属市场中,黄金市场是发展最早、最完善以及规模最大的市场。2006—2011年间,黄金的平均日交易规模为325亿美元,而白银、铂金和钯金则分别为45亿美元、8亿美元和1亿美元[30],远小于黄金。因此黄金市场整体的有效性较其他贵金属市场要强,也比较能经受得住外来冲击的影响。而钯金市场在四个贵金属市场当中最晚出现,同时也是发展最不完善的市场,因此,在样本期间内市场整体的有效性程度相对最低,也比较容易受到外来冲击而偏离有效市场。第二,ETFs的出现方便了黄金的投资并刺激了黄金的需求,加上黄金在ETFs上的绝对地位,使得投资者更加容易获取与决策有关的信息。因此,较高的市场有效性可能说明了黄金在全球金融市场上占有重要地位,反映了其在投资方面的吸引力以及作为风险管理工具的能力。类似的,较低的有效性可能说明钯金吸引投资的能力相对较弱,在全球金融市场中的重要性要相对低于其他几个贵金属市场。
5.结论与建议
本文基于1987年3月至2016年12月伦敦金属交易所的四种贵金属(黄金、白银、铂金和钯金)现货价格数据,采用time-varying AR模型对贵金属市场的时变有效性进行了分析。研究结论如下:
(1)根据全样本静态检验的结果,四个贵金属市场都是弱式有效市场。这表明从静态的角度来看,贵金属市场上的投资者采取被动消极的投资策略即可。
(2)根据TV-AR模型的研究结果,四个贵金属市场的有效性均会随着时间的推移而发生改变,并且经济政治环境的变化是造成贵金属市场偏离有效市场的重要原因。在偏离有效市场之后,市场有逐渐回复到有效市场的趋势。实证结果表明特定时段的市场有效性会由于经济或者政治环境的变化而出现暂时性的下滑,从而偏离有效市场。此时的市场存在收益可预测性,投资者可以采取主动投资策略来获取超额收益。结合结论(1)可以发现,贵金属市场的有效性并非总是一成不变的,即便是长期来看达到弱式有效的市场,可能也会在特定时期由于经济或政治事件的冲击而偏离有效市场。所以,建议贵金属市场上的投资者采取动态的投资策略,依据金融环境的改变而进行适应性的变化,即类似于股票市场上的事件驱动型交易策略[31]111-126:在具有重大影响的经济政治事件爆发使得贵金属市场偏离有效市场时,采取主动的投资策略;当事件爆发一段时期之后市场重新达到弱式有效时,则采取被动的投资策略。同样的,有关贵金属市场效率的研究也应该采取动态的视角,避免样本选取对检验结果产生干扰,从而更加准确地考察市场效率。
(3)由四个市场有效性程度指标的对比分析可以发现,黄金市场有效性程度指标的均值和波动幅度要明显小于其他三个白色贵金属市场,而钯金市场的均值和波动幅度则相对最大。这可能与贵金属市场的发展程度及其在全球金融市场中的地位有关。此外,贵金属市场的有效性可能与其在全球金融市场中的地位有关,反映了贵金属吸引投资以及作为风险管理工具的能力。实证结果表明,就全球金融市场中的重要性而言,应该是:黄金市场>白银市场>铂金市场>钯金市场。所以,AMH理论也为研究这些贵金属在投资(全球金融市场)当中的重要性提供了一种思路。
——庆祝中国共产党成立一百周年贵金属纪念币展

