七桥问题
2019-11-13 03:45马兆兵摘编
初中生世界 2019年37期
文 马兆兵(摘编)
18世纪初,在波罗的海南海岸有一座景色迷人的小镇——普鲁士的哥尼斯堡(现在叫加里宁格勒),被一条河穿过。河中有两个小岛,有七座桥把两个岛与河岸连了起来(如图1)。这里的桥和景色每天都吸引了无数的游客流连忘返。
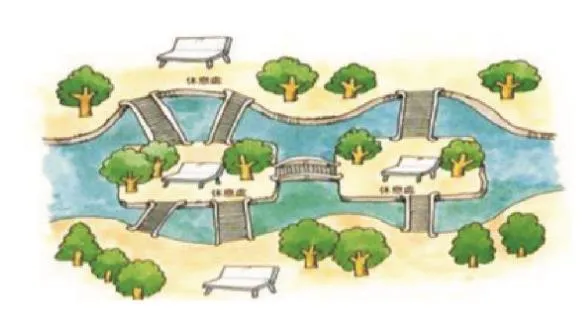
图1
城中有位聪明、爱思考的少年。一天,这位少年提出了这样一个问题:一个人能否从某地出发,穿过所有桥不重复、不遗漏地一次走完七座桥,最后回到出发点?
问题提出后,很多人对此感兴趣,纷纷进行试验,但在相当长的时间里,始终未能解决。因而,这个问题在那时成了一道著名的难题,也就是“哥尼斯堡七桥问题”。
1735年,有几名大学生写信给在彼得堡科学院任职的天才数学家欧拉,请他帮忙解决这一问题。欧拉实地观察之后,认真思考走法,但始终没能成功。
欧拉思考:人们多次失败是否预示着这样的路线根本不存在?该如何说明呢?
欧拉用数学分析法,将其中的四块陆地抽象为四个点A、B、C、D,将陆地之间架设的七座桥梁用线来表示,分别表示为a、b、c、d、e、f、g。经过抽象之后,图1就变成了由点和线组成的图形(如图2),这个图形被称为“欧拉图”。于是,“七桥”问题就转化为是否可以“一笔画”的问题。什么叫“一笔画”呢?那就是笔不准离开纸,一笔画成整个图形,且每一条线只许画一次,不得重复。
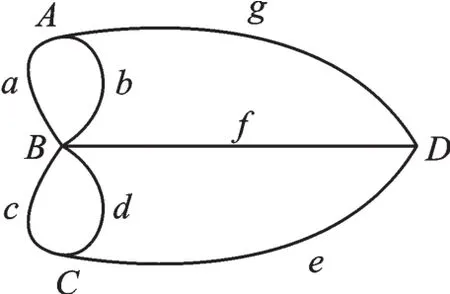
图2
接下来,欧拉找到了“一笔画”的规律,并以此规律为判断准则,很快就判断出:要一次不重复地走遍哥尼斯堡的七座桥是不可能的。也就是说,这么多年来,人们费脑费力寻找的那条不重复的路线,根本就不存在。
欧拉的思考方法非常巧妙,也非常重要,它正表明了数学家处理实际问题的独特之处——把一个实际问题抽象成合适的“数学模型”。这种研究方法就是“数学模型法”。
猜你喜欢
车主之友(2022年4期)2022-08-27
卫星应用(2022年3期)2022-05-23
世界建筑导报(2022年1期)2022-04-22
哈哈画报(2022年1期)2022-04-19
车迷(2022年1期)2022-03-29
文苑(2020年8期)2020-09-09
中国品牌(2019年10期)2019-10-15
北京心理卫生协会学校心理卫生委员会学术年会论文集(2018年1期)2018-05-10
祝您健康(1982年5期)1982-12-29

