高技术产业与经济增长关系的动态演变研究

陈绍刚，易彩君，曾 翎

(电子科技大学数学科学学院，四川 成都 611731)

研究高技术产业内部发展规律，探索其与经济的关系，对政府的宏观调控、国民经济的健康发展都是至关重要的，近年来人们对高技术产业相关问题的研究逐步深入，如牛勇平、刘光彦通过分析发现高技术产品出口是带动我国经济增长的重要因素[1].随后赵玉林运用灰色关联方法发现高技术产业与经济增长最为密切，认为大力发展高技术产业是经济增长稳定的关键战略[2]；钟鸣长等发现高技术产业对传统产业溢出作用明显[3].由于早年缺少足够的数据，上述文献并没有运用相关模型测算出高技术产业对经济增长的具体贡献值，数据逐渐完善后，赵健运用多元回归方法对数据进行分析，发现高技术产业具有明显的发展优势与前景[4].可见高技术产业与经济增长密不可分，对经济结构的调整有很大的影响，是研究经济增长的一个重要切入点.高技术产业与经济增长的静态研究日益成熟，相关研究者开始对两者关系的趋势进行研究.张华平对我国高技术产业与经济增长之间的关系进行动态检验[5].之后张进铭、高雪萍发现，在江西省高技术产业发展对经济增长的带动作用在逐渐加大[6].文献中对高技术与经济增长关系的趋势进行初步探索，但是并不全面，都是比较粗略的判断.随后苏娜对高技术产业与区域经济协调发展问题进行了全面系统的研究[7]；系统的研究能更好地发现问题与解决问题.张彩江发现银行集聚和证券集聚可以显著地促进高技术产业创新效率的提高[8]；给解决高技术创新效率问题提供一个突破口.但与大多数人的结论不同的是，蔡锋伟经过实证分析认为高技术产业对经济增长的贡献并不大，而反过来，经济增长对高技术产业的贡献很大[9]，两者之间的关系需要进一步研究.管理，政策等多种因素使得经济发展产生地域性差异，人们开始研究高技术产业与区域经济间的关系如：李秉宪发现高技术产业对区域经济发展的推动作用呈不断扩大趋势[10]. 随后李洪伟、任娜发现中国东、中、西部地区的高技术产业发展与经济增长之间的关系有显著的地区差异[11]. 文献中从空间角度出发研究两者之间的关系，并在区域间检验出显著的差异，那么从时间角度研究其是否有差异性是很有必要的，也是急需填补的知识空缺.

很多研究证明菲德模型能有效地测量高技术产业对经济增长的贡献系数.张平发现关于技术进步对经济增长贡献的测度模型已不能有效地解释基于信息技术的高技术对经济增长的贡献，于是提出运用菲德模型进行测量[12].之后李津运用菲德模型，探讨了劳动力、资本、高技术产业的效应对社会总产值与传统产业之间的差异性[13]. 戴志敏等运用菲德模型对江西省高新技术产业的溢出效应进行了实证检验[14].进而华锐、庄子银将其运用到研发领域中，并分离出研发的直接效应和溢出效应[15]. 运用菲德模型能探索不同的衡量指标，如高技术产业对经济增长的总贡献，直接贡献，外溢效应，以及高技术产业与非高技术部门的要素边际生产率差异，这是以往测度模型难以做到的.

高技术产业对经济增长的总贡献可以称为贡献系数，而贡献系数又分为直接效应和外溢效应. 直接效应即高技术产业产出直接促进经济的增长；而外溢效应是高技术产业通过影响非高技术产业进而促进经济的增长.目前研究高技术产业与经济增长关系的方法主要是线性模型，多数文章在探索高技术产业对经济增长的贡献时一般先构建菲德模型或根据生产函数如：柯布—道格拉斯和C -D 生产函数，然后采用古典线性回归，根据回归方程的系数，判断高技术产业的贡献系数大小及正负情况；总的结论是高科技产业促进经济的增长；高新技术产业的发展是拉动经济增长的重要因素. 然而，对于高技术产业是如何促进经济增长的还没有特别突出的研究，研究高技术产业对经济增长的贡献系数的变化情况，可以进一步了解高技术产业与经济增长的系统机制，而变参数模型中的状态方程能很好地反应参数随时间变化的情况，因此本文将菲德模型与变参数模型相结合，构建高技术产业对经济增长贡献的动态变化模型，进一步了解其对经济增长贡献的趋势及其稳定状况.

1 模型构建

1.1 菲德模型

菲德模型最初应用在出口与经济增长的关系中，按照菲德德思想，出口对经济增长中的作用可分为直接效益和间接效益，根据生产函数，菲德模型能有效地度量出口对经济增长的直接效应和间接效应[16].由于菲德模型成功地解释了出口对经济增长的贡献，其分析框架得到了广泛的应用[17]. 借鉴菲德的两框架思想，本文将经济部门简单地分为高技术产业部门与非高技术产业部门，最后建立以下生产函数：

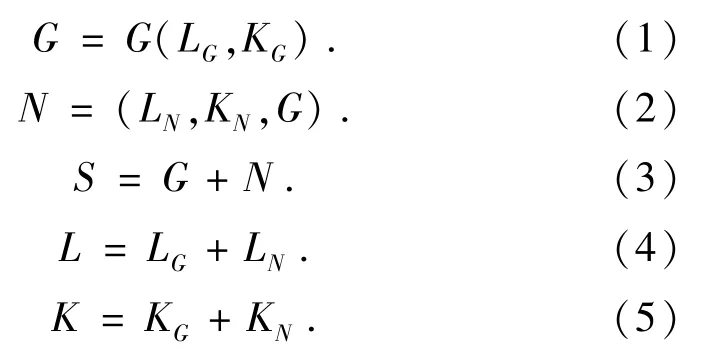
借鉴Bruno[18]的假设有

其中S 代表社会总产值， G 表示高技术产业部门，N 表示非高技术产业部门，LG为高技术产业部门劳动力投入，KG为高技术产业资金投入. 相应地LN为非高技术产业部门劳动力投入， KN为非高技术产业资金投入； σ 是两个部门间相对边际生产力的差异，σ 大于0 说明边际生产力从非高技术部门流入高技术产业部门，σ 小于0 说明边际生产力从高技术部门流入非高技术产业部门. 对(3)式进行求导并将(4)(5)(6)式代入得：

模型中假设非高技术部门的产出弹性系数不变；两边同除以S 推导出以下方程：

按模型假设，方程中的各个系数不变并且有

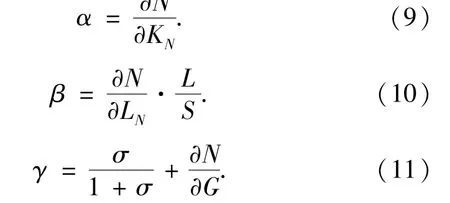
其中α 为非高技术部门资本的边际产出；β 为非高技术部门劳动力的弹性系数；γ 为高技术产业对经济增长的所有贡献，包括直接贡献和间接贡献. 若γ＞0 说明高技术产业贡献系数促进经济增长，若γ ＜0 则说明高技术产业效应阻碍经济增长. γ 值的大小对应高技术产业对经济增长的贡献大小.

1.2 变参数模型

运用古典线性回归估计高技术产业对经济增长的贡献固然可以，但是随着时间变化，经济结构的不断改变，外界的种种冲击，政策改革等，经济变量之间的关系也可能会发生改变.于是考虑运用变参数模型探索高技术产业对经济增长贡献的动态变化.变参数的状态空间模型如下：

其中假定ut和εt服从均值为0 方差为σ2和协方差矩阵为Q 的正态分布[21]即有：

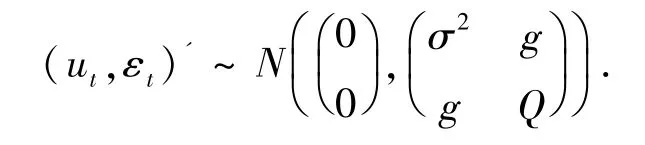
且有cov(ut，εt) = g，将菲德模型与变参数模型结合起来得：

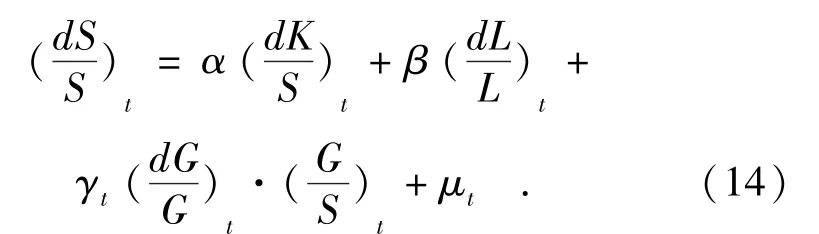
贡献系数γt的状态方程设定为一阶自回归模型即：γt= φγt-1+ εt，其中分别表示国民总产值增长率，劳动增长率，高技术产业产值增长率，资产增长与国民总产值的比例， α 与β 为固定参数，γt是会随着时间变化的时变参数，是反映高技术产业与经济增长贡献的动态指标.

2 数据处理与分析

2.1 数据来源与指标选取

表1 数据来源于《中国统计年鉴》和《中国统计局》.根据(14)式对原始数据进行处理时，消去了量纲对模型的影响，因此文章中的各个变量不进行归一化处理，而是根据模型表达式处理各个时间序列. 本文根据菲德思想所建立的变参数模型中S 用国内生产总值作为代表变量， L 为劳动力投入，用全国就业人数作为代表变量，K 为资金投入用全国固定资产投资作为代表变量，为了数据的完整性和结果的准确性G 变量采用高技术产业主营业收入替代.

表1 各个指标原始数据Table 1 Raw data of each indicator

2.2 平稳性检验与协整检验

为了使得实证的结果更加可靠，并避免伪回归，在进行数据分析前需要对各个变量的时间序列进行平稳性检验.本文采用ADF 方法检验各个时间序列的平稳性，经检验发现，各个变量的时间序列是非平稳的，一阶差分后在0.005 水平下均为平稳序列，检验结果见表2. 各个变量的时间序列自身是非平稳的，但在一阶差分后是平稳序列，若其线性组合存在长期稳定的均衡关系，称变量间具有协整关系[19]；本文采用单位根检验法，发现各个变量是一阶单整序列，所选时间序列可以进行变参数模型分析.

3 模型结果及实证分析

3.1 高技术产业发展现状分析

20 世纪80 年代，高技术产业的迅速兴起与发展给世界经济、军事、政治带来了深刻的影响. Lawrence M.Rausch 认为高技术产业的相关产品的全球市场增长速度是其他制成品的两倍多，并推动全球经济增长.如今，高技术产业已经成为衡量一个国家综合国力的重要指标，也是经济增长的主要动力之一[20-21].自改革开放以来我国高技术产业日益壮大，在国民经济中扮演着越来越重要的角色，1995 年到2012 年，高技术产业总产值明显放大，由1995 年的4 098 亿元增长到2012 年的77 399 亿元，平均每年翻了一翻，其主营业收入由1995 年的3 917 亿元增长到2016 年的153 796 亿元，平均每年增长1.7 倍.衡量高技术产业发展的各个指标在增长，而国内生产总值几乎每年也在增长这是否说明高技术产业的增长带动经济的增长；还是经济的增长促进高技术产业的蓬勃发展；这是非常值得研究的两个问题.由图1 可以看到高技术产业与GDP 之间的百分比随着时间的增长出现一定的波动，但从整体来看是呈现上升趋势的，两者的百分比由1995 年的6.4%增长到2016 年的20.6%，在短短22 年内高技术产业在中国迅速发展. 面临1997年后的通货紧缩，其主营业收入与GDP 的百分比并没有下滑，在2008 年金融危机后有所回降；但幅度并不大，可见高技术产业具有充沛的生命力，对经济的稳定增长具有特殊的贡献.于是本文收集高技术产业与国内生产总值的相关宏观数据，通过分析与整理基于菲德思想建立变参数模型以进一步探索两者之间的关系.

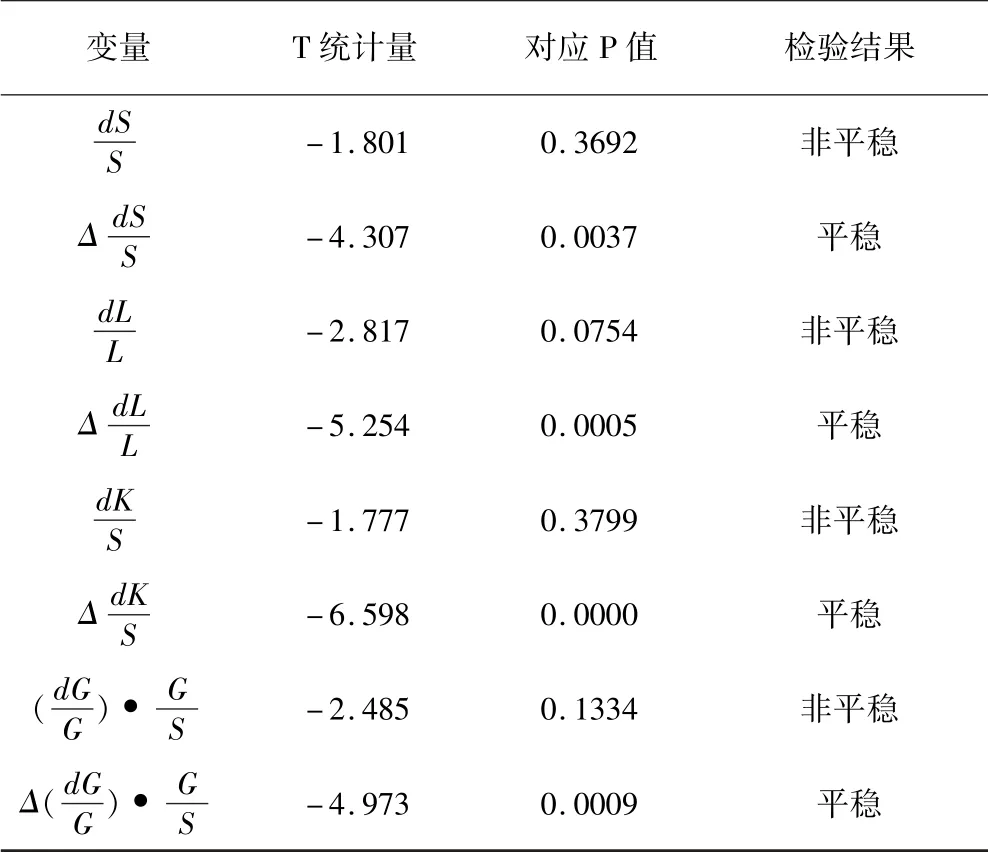
表2 各个时间序列平稳性检验Table 2 Stationarity test of each time series

图1 高技术产业主营业收入占GDP 的百分比Fig.1 The proportion of the main operating income and GDP of high-tech industries

3.2 高技术产业与经济增长关系的动态演变的实证分析

将各个指标代入变参数模型，运用卡尔曼滤波算法估计状态方程，结果显示各个回归系数显著，R 方高达0.987，拟合效果较好，本文主要关注的是高技术产业对经济增长的贡献系数即γt，根据模型估计结果绘制γt的图像，发现贡献弹性系数在不同时间段内出现较大波动，根据γt增减情况将其分成两个阶段如图2、图3.第一阶段即1996 ～2004 年，其出现较大幅度的递减现象，贡献弹性系数由1996 年的0.876 下降到2004 年的0.170，前4 年下降速度较大，出现这一趋势的一个原因可能是：我国高技术产业受稀缺生产要素的限制.虽然我国高技术产业发展很快，但关键技术还掌握在发达国家中，创新能力、自主研发能力不足并且关键性人才稀缺，企业需要花大量的资金补上这些短板，随着企业长时间的发展，高投入并没有按一定比例高产出.另一方面可能是由高技术企业本身的性质所决定的，高技术产业是一个高收益高风险的行业，由于其高创新性，技术开发，生产开发，市场开发等存在诸多不确定性，对风险投资依赖性很强，高技术产业在不同阶段对资金都有不同的需求，创办高技术产业的成本是传统产业的10 到20 倍，而成功率相对较低[19]，也有可能导致其贡献值的阶段性下降.

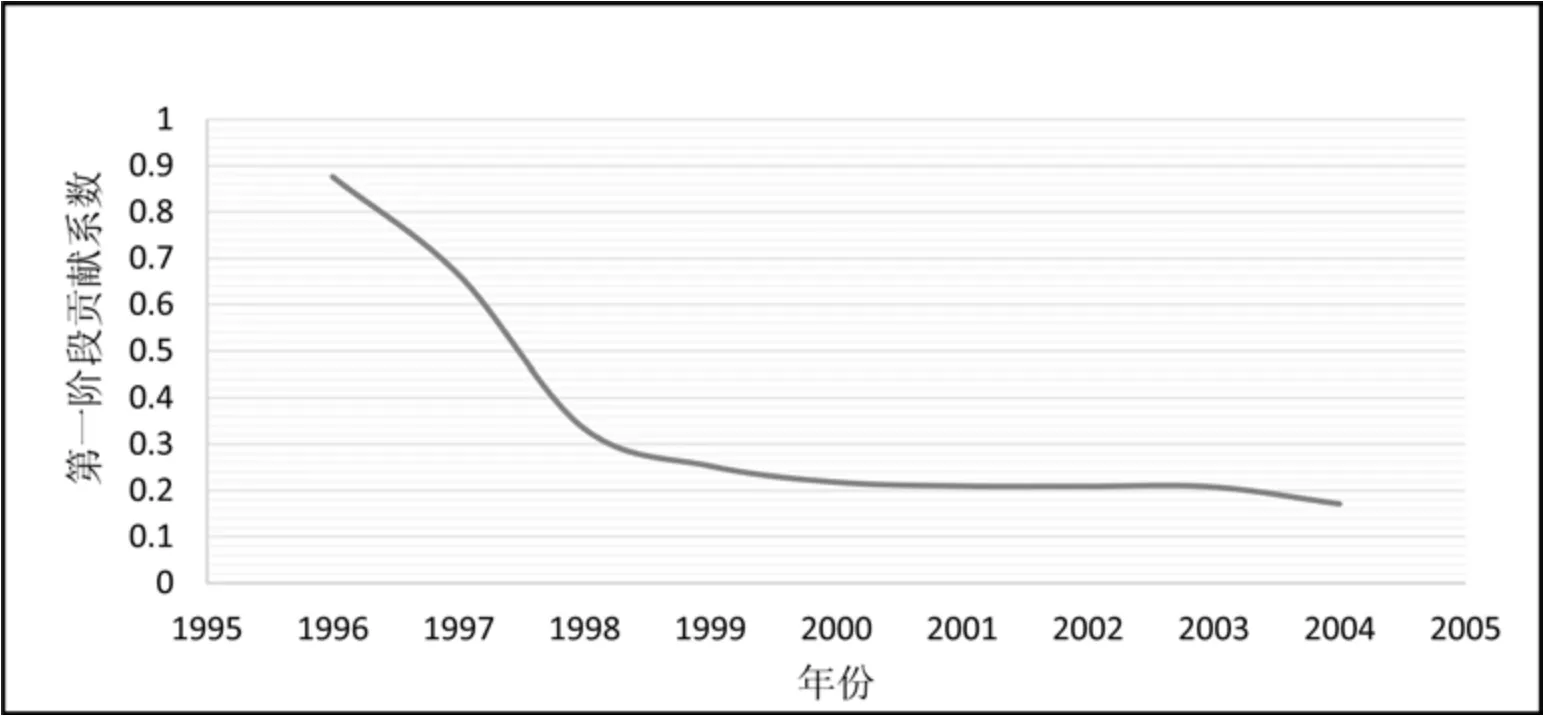
图2 第一阶段高技术产业对经济增长的贡献弹性系数趋势Fig. 2 The contribution of the first stage high-tech industry to economic growth

第二阶段即2005 年到2016 年，其贡献弹性系数变化如图3，由曲线图可以看出，贡献弹性系数出现一定的波动，呈现“波浪”型曲线，但波动幅度不大，2005 年到2009 年处于上升趋势，2009 年达到峰值，可见高技术产业对经济增长的贡献在2008 年发生金融危机时也没有下滑，多年来我国没有出现严重的经济衰退，高技术产业的高速成长是一个重要的决定因素.2010 年弹性系数有所回降，但下降程度较小，之后曲线逐渐趋于平稳；第2 阶段总体上是处于上升趋势但上升的速度较慢.所选取的时间序列内高技术产业对经济增长的贡献系数都为正，说明高技术产业在长时间内促进经济的增长.从实证分析的结果中我们发现高技术产业在宏观经济运行和经济结构调整中产生了前所未有的影响，是经济增长稳定的关键因素.

图3 第二阶段高技术产业对经济增长的贡献弹性系数趋势Fig. 3 The contribution of the second stage high-tech industry to economic growth

4 结论及启示

4.1 结论

本文基于1995 ～2016 年的相关数据利用菲德思想与变参数模型，构造测量高技术产业与经济增长关系的动态变化模型，间接反应经济结构变化，及社会冲击等因素对高技术产业拉动经济增长贡献的影响.从理论模型及实证分析中，本文得出以下几个结论：

1)高技术产业发展与经济增长关系存在长期的均衡关系；

2)高技术产业对经济增长的贡献弹性系数大体归为2 个阶段：第1 阶段1996 ～2004 年呈下滑趋势，且前4 年递减速度较快；第2 阶段2005 ～2016 年出现一定的波动但总体趋势是在上升，但增长幅度较慢.

3)高技术产业对经济增长的正作用逐渐趋于平稳状态.

4.2 启示

改革开放以来我国高技术产业发展迅速，但是我国的高技术产业与国外相比还存在较大的差距，国内很多高技术产业还处在模仿和探索阶段，很多关键性技术对外依赖性极高，大多数都依靠进口，我国高技术产业面临的最大障碍是缺少创新能力和自主研发能力，很多研究过多注重理论意义，缺少实际可行性.并且很多研究新方向仍然处于模仿阶段，因此我国政府应该大力培养自主创新能力人才，改善培养人才方式，使我国高技术产业更加健康地成长，关键技术不受制于人，也为我国经济长远稳定发展奠下基础. 其次我国的高技术产业R＆D 投入虽然每年都在增加，但是投入强度不高，发达国家的R＆D 与GDP 的百分比高达20%，而我国仅在6%左右[20]，中国可以加大R＆D 投入突破瓶颈，为大力发展高技术产业打下稳定的基础.