递归神经网络方法解决非光滑伪凸优化问题

喻 昕 胡 悦 马 崇 伍灵贞 汪炎林

(广西大学计算机与电子信息学院 广西 南宁 530004)

0 引 言

近年来，由于人工神经网络内在的大规模并行机制以及快速执行的硬件结构，其执行效率显著优于传统优化算法，这让使用人工神经网络解决优化问题成为了当下的热门研究对象。运用神经网络求解最优化问题，首先要将目标函数改换成相关动力学模型，进而构造出解决该问题的神经网络模型。神经网络是由Tank等[1]最先应用到优化问题的。自此，研究者们开始构造更多模型用于解决优化问题。

目前，关于最优化问题的研讨大都局限于光滑优化问题，然而，在实际应用问题的研究上，逐渐出现了很多非光滑问题。因此学者们设计了很多解决非光滑优化问题的方法，文献[2]通过微分包含的思想创建了一个新型模型用以解决非光滑优化问题。文献[3]构造了一个递归双层模型来解决非光滑凸优化问题，该模型虽不含惩罚算子，但是层次稍显复杂。

凸优化问题[3-7]在许多问题上具有非常广泛的使用背景，但是随着更深入的研究，学者们逐渐发现非凸优化问题在工程问题中有着更好的应用。因此，部分学者成功构造了可以解决目标函数为非凸的相关问题的模型。如文献[8]根据梯度思想创建了一种神经网络模型用以解决非光滑非凸问题，该模型结构简单，但是需要一个惩罚算子，这限制了该模型的使用范围。

伪凸优化问题为非凸优化问题的一类，也成了热门研究对象[9-13]。为了解决非光滑伪凸优化问题，文献[9]创建了一个层次仅为一层不需要提前计算惩罚算子的新型神经网络模型， 但是这个模型需要很强的假设条件，且仅仅可以解决带有等式约束的问题，这就大大减少了其应用范围。为了解决同时具备等式约束以及方体约束且目标函数是伪凸的优化问题，文献[10]应用惩罚函数创建了一个层次仅为一层神经网络模型，该模型能够较好的收敛，但需要用到惩罚算子，这在实际计算中是很难解决的。为了能够不用计算惩罚算子，文献[11]提出了一种新型且不带惩罚参数的单层模型，并得出了该单层模型的解在一定的条件下可以在一定时间内收敛到可行域的结论，该模型可以较好的收敛，但是需要目标函数存在下界等条件。

本文创建了一种新型的递归神经网络模型，该模型包括以下优点：(1)可以求解目标函数为非光滑且伪凸的问题；(2)模型结构简单，为单层递归神经网络；(3)不依赖于惩罚参数；(4)可以求解同时带等式约束和不等式约束的问题。

本文将研究下面的非光滑伪凸优化问题：

minf(x)

s.t.Ax=bg(x)≤0

(1)

式中：x=(x1,x2,…,xn)T∈Rn，A∈Rm×n是行满秩矩阵，b=(b1,b2,…,bm)T∈Rm，f(x):Rn→R是伪凸函数且局部Lipschitz连续，gi(x):Rn→R是凸函数。设S1={x∈Rn:gi(x)≤0,i=1,2,…,m}S2={x∈Rn:Ax=b}，则式(1)的可行域为S=S1∩S2。

1 预备知识

下面给出部分与后文相关的定义与引理，以方便理解。

定义1对于函数f:Rn→R，若存在正数κ和ε，对于所有的x1,x2∈x+εB(0,1)，满足:

|f(x2)-f(x1)|≤κ‖x2-x1‖

那么称函数f(x)在x∈Rn处是Lipschitz连续，其中B(0,1)是Rn上的一个开球。如果函数f(x)在其定义域上的每一点都满足Lipschitz连续，那么这样的函数称为局部Lipschitz函数。

定义2设对于集合E⊂Rn上的任意点x，都有一个相应的非空集合F(x)⊂Rn，则x→F(x)是E→Rn上的集值映射。如果对于任意的开集V⊃F(x0)，都存在x0的一个邻域U，使得F(U)⊂V，则称集值映射F:E→Rn在点x0∈E是上半连续。

定义3设函数f在点x附近是Lipschitz的，则f在点x处沿方向v∈Rn的广义方向导数为：

另外，f在点x处的Clarke广义梯度定义为：

∂f(x)={ξ∈Rn∶f0(x∶v)≥,∀v∈Rn}

如果f在点x0处是局部Lipschitz连续的，记Lipschitz常数为κ，则∂f(x0)为Rn中的非空紧凸子集，并且对∀ξ∈∂f(x0)，都有‖ξ‖≤κ。

性质1[9]设f∶Rn→R是凸函数，则有如下性质：

∂f(x0)={ξ∈Rn∶f(x0)-f(x)≤〈ξ,x0-x〉,∀x∈Rn}∂f(·)是极大单调的，即对任意的v∈∂f(x)和v0∈∂f(x0)，有〈x-x0,v-v0〉≥0。

定义4如果一个函数f:Rn→R，在点x附近是局部Lipschitz，那么当它满足以下的两个条件时，称它在x附近是正则函数。

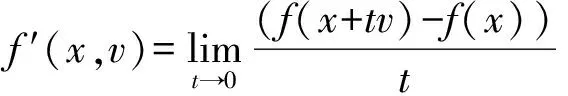
(2) ∀v∈Rn，f′(x,v)=f0(x,v)。

定义5设E⊂Rn是一个非空凸集，称函数f:E→R为集合E上的伪凸函数，是指对任意的x,y∈E，若存在η∈∂f(x)，使得ηT(y-x)≥0，则必有f(y)≥f(x)。

引理1链式法则。设F(x)∶Rn→R是正则的，并且x(t)∶[0,+∞)→Rn在[0,+∞)上的任何紧区间上都是绝对连续的，则对t∈[0,+∞)，x(t)和F(x(t))∶[0,+∞)→R是几乎处处可微的，并且有：

2 递归神经网络

2.1 定 义

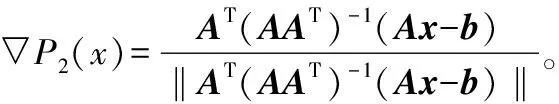
当x∈S2，∂P2(x)={AT(AAT)-1Aζ：‖ζ‖≤1}。

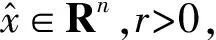
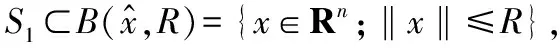
引理2[11]如果假设1成立，那么:

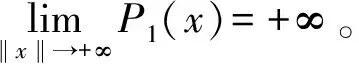
(2)X=M，其中X={x∈Rn:g(x)≤0}，M={x∈Rn:G(x)≤0}。

式中：I0(x)={i∈{1,2,…,m}:Gi(x)=0}，I+(x)={i∈{1,2,…,m}:Gi(x)>0}。

针对非光滑伪凸优化问题，本文构造了如下死亡新型递归神经网络模型：

(2)

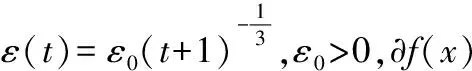
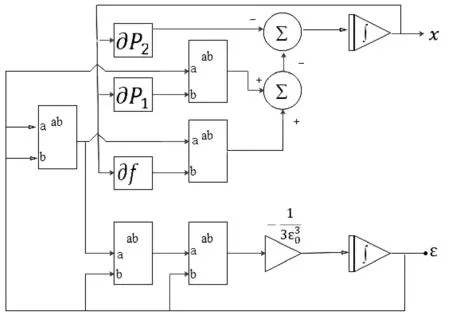
图1 递归神经网络模型(2)的网络硬件实现结构图

定义6称向量函数x(·)为式(2)过初始点x(0)=x0的状态解，若x(t)绝对连续，并对几乎所有的t都有:

定义7如果对所有的t都有：

0∈-∂P2(x*)-ε(t)∂P1(x*)-ε2(t)∂f(x*)

则称x*为式(2)的一个平衡点。

2.2 全局解的存在性

引理4如果假设1和假设2均满足，则式(2)具有局部解x(t)，且x(t)有界。

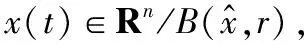
定理1对于任意的初始点x0∈Rn，式(2)至少存在一个全局解x(t)，且x(t)是有界的。

证明由引理4可知式(2)存在有界局部解，根据解的扩展性理论，可知式(2)存在全局解x(t)，t∈[0,+∞)。类似引理4，可证明全局解x(t)有界。

2.3 递归神经网络的收敛性

定理2过任意初始点的式(2)的解均能在有限时间内进到等式约束集S2，并永驻其中。

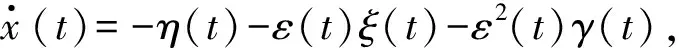
-‖η(t)‖2-ε(t)ξ(t)Tη(t)-ε2(t)γ(t)Tη(t)≤

-‖η(t)‖2+ε(t)‖ξ(t)‖‖η(t)‖+

ε2(t)‖γ(t)‖‖η(t)‖

(3)

当x(t)∉S2时，‖η(t)‖=1。

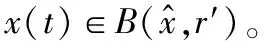
‖∂f(x(t))‖∶=sup{‖γ‖∶γ∈∂f(x(t))}∶lf∀x∈B(x,r′)

同理，对于强制的凸函数P1(x)，存在lp>0，使得:

‖∂P1(x(t))‖∶=sup{‖ξ‖∶ξ∈∂P1(x(t))}≤lp∀x∈B(x,r′)

综上，当x(t)∉S2，有：

(4)

若x(T1)∈S2，则T1大于等于x(t)收敛到S2的时间点。

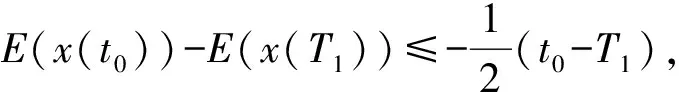
0≤‖AT(AAT)-1(Ax(t0)-b)‖≤

(5)

解以上不等式可以得到:

t0≤2‖AT(AAT)-1(Ax(T1)-b)‖+T1

这意味着，当t>2‖AT(AAT)-1(Ax(T1)-b)‖+T1，必有x(t)∈S2。即状态解x(t)将在一定时间进入等式约束集S2={x∈Rn|Ax=b},且该上限为:

t0=2‖AT(AAT)-1(Ax(T1)-b)‖+T1

综上，过任意初始点x0∈Rn的状态解x(t)必将在有限时间内进入等式约束集。

接下来将证明式(2)的状态解x(t)一旦进入等式约束集S2，就会一直在S2内。若非如此，假设状态解x(t)在t1时刻离开等式约束集S2，则一定存在区间(t1,t2)，t1>T1，使得对任意的t∈(t1,t2)都有x(t)∉S2，且‖AT(AAT)-1(Ax(t1)-b)‖=0。再结合式(5)，可以得到：

‖AT(AAT)-1(Ax(t2)-b)‖≤

这与‖AT(AAT)-1(Ax(t2)-b)‖>0矛盾。

因此式(2)的状态解x(t)在有限时间里进入到等式约束集S2，并永驻其中。

引理6[4]

1) 对于所有x∈Rn，ξ2∈∂P2(x)，有：

2) 对于任意x∈S2/S1，ξ1∈∂P1(x)，有：

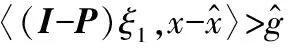
3) 对于任意x∈S2/S1，ξ1∈∂P1(x)，有:

证明

1) 因为当x∈S2， ∂P2(x)={AT(AAT)-1Aζ：‖ζ‖≤1}则:

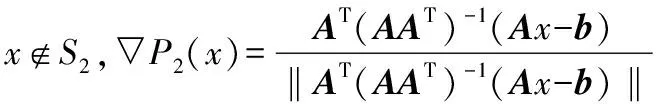
定理3如果假设满足，则式(2)从任意一点出发 的状态解将在有限时间内进入不等式约束集S1={x∈Rn:g(x)≤0},并永驻其中。

ξ(t)T·[(I-P)(-ε(t)ξ(t)-ε2(t)γ(t))]

又因为(I-P)T=I-P且(I-P)2=I-P有：

ε2(t)‖(I-P)ξ(t)‖‖γ(t)‖

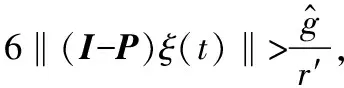
若x(T2)∈S1，则T2大于等于x(t)收敛到S1的时间点。

若x(T2)∉S1有:

(6)

然后对式(6)两边从T2到t进行积分得到：

用反证法，若不在有限时间内进入S1，则当t→+∞可得:

类似于定理2，我们可以证明得到一旦神经网络的状态解进入到S1将永驻其中。

综上可得，式(2)从任意一点出发的状态解x(t)将在有限时间内进入不等式约束集S1={x∈Rn∶g(x)≤0},并永驻其中。

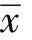
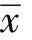
(7)

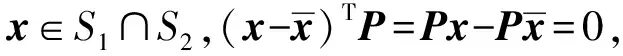
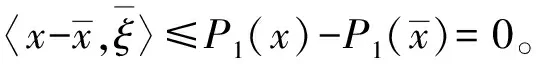
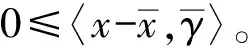
又由f(x)是伪凸的，可知：

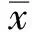
引理8[11]设x*是式(1)的一个最优解，则对于任意的x∈S1∩S2和γ∈∂f(x)，有：

〈γ,x-x*〉≥0

定理4若假设1、2均满足，式(2)至少有一个平衡点，且式(2)从任意点出发的状态解x(t)均收敛到式(1)的一个最优解。

证明设x*是式(1)的一个最优解。定义Lyapunov函数如下：

V(x,t)=ε2(t)[f(x)-f(x*)]+

(8)

经过简单的计算可得:

∂V(x)=ε2(t)∂f(x)+ε(t)∂P1(x)+x-x*

任取x0∈Rn，设x(t)为式(2)过初始点x0的状态解。另外，由定理2和定理3可知，式(2)的状态解x(t)在一定时间内进入到等式约束集S1和不等式约束集S2，并永驻其中。因此，不失一般性，我们假设：

x(t)∈S=S1∩S2∀t≥0

类似于引理4的证明，存在可测函数ξ(t)∈∂P1(x(t))，γ(x(t))∈∂f(x(t))，对于a.e.t∈[0,+∞)，满足：

(9)

由x(t)，x*∈S1可知，P(x(t)-x*)=0，∀t≥0。由引理1和式(I-P)2=I-P可知，对于a.e.t∈[0，+∞)，有：

-‖(I-P)(ε(t)ξ(t)+ε2(t)γ(t))‖2-

〈x(t)-x*,ε(t)ξ(t)+ε2(t)γ(t)〉+

(10)

由引理8可知:

0≤〈γ(t),x(t)-x*〉

由凸不等式知:

〈x(t)-x*,ξ(t)〉≥P1(x(t))-P1(x*)=0

令ψ(x(t))=ε2(t)∂f(x)+ε(t)∂P1(x)，因此：

(11)

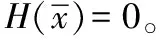
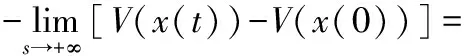
V(x(0))-V0<+∞

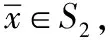
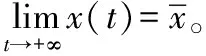
(12)

3 仿真实验

为了检验上述理论的正确性，下面将利用递归神经网络来求解二类优化问题并列举几个数值实例来验证。仿真实验在MATLAB 2012a平台下进行。

实验1带有等式和方体约束的非光滑伪凸优化问题：

(13)

s.t.Ax=b-1≤xi≤1i=1,2

式(13)的目标函数是高斯函数。高斯函数是一种局部Lipschitz连续且在Rn上是严格伪凸的，且在随机优化中占有重要的地位。文献[9-10]分别提出了两类神经网络来解决这类问题，但文献[9]的神经网络仅能解决带等式约束的问题，而文献[10]可以解决上述问题，却需要提前计算惩罚参数。本文构造的递归神经网络模型可以克服上述两个缺点。

针对式(13)，取A∈R2,b∈R,σ=(σ1,σ2)=(1,1)T,A=[0.523,0.917],b=0.623。任取4个不同的初始点(0,1.5)、(0,0)、(-1,-2)、(5,6)，仿真实验结果如图2所示。可以看出递归神经网络从任意初始点出发的状态解都能收敛到式(13)的一个最优解x*=(0.436 5,0.436 5)。

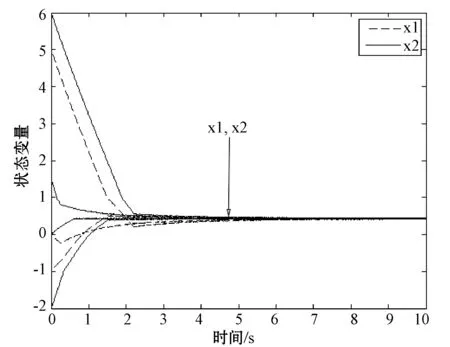
图2 实验1的任意4个初始点的x(t)的收敛轨迹

实验2带有等式和不等式约束的凸优化问题。

凸函数是具有重要实际意义的函数，式(2)也能够解决目标函数伪凸函数且带有等式和不等式约束的问题：

(14)

s.t.x1+x2=1

-xi≤0i=1,2

式(14)是一类常见的凸优化问题，很多研究者构造了多种神经网络来解决此类问题，但这些模型大都必须包含惩罚参数，或是结构会相对复杂。本文构造的递归神经网络模型能够避免上述缺点。

基于上述问题，通过MATLAB进行模拟实验，随机取4个初始点(0,1.5)、(0,0)、(-1,-2)、(5,6)，实验结果如图3所示。可以看出，对任意初始点递归神经网络的状态解都将收敛到非线性凸问题的一个最优解x*=(0,1)T。

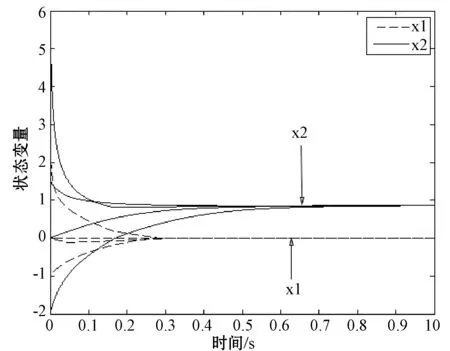
图3 实验2的任意4个初始点的x(t)的收敛轨迹

4 结 语

本文创建了一种解决非光滑伪凸优化问题的新型递归神经网络模型。与以往的模型相比较，本文提出的模型层次仅为单层，且不用依赖于惩罚参数的选取，同时还能够解决同时带有等式约束和不等式约束的优化问题。本文主要证得了状态解有全局解，且能够在有限时间内收敛到原目标函数的可行域，最终收敛到伪凸优化问题的最优解等重要理论。同时，通过两个实验验证了该模型的正确性。