基于有限元方法的正交各向异性形变体仿真设计

石跃祥 胡 维

1(湘潭大学信息工程学院 湖南 湘潭 411105)2(LED照明驱动与控制应用工程技术研究中心 贵州 铜仁 554300)

0 引 言

基于有限元方法的正交各向异性形变体的仿真广泛应用在影视动画、游戏特效、虚拟现实等领域中，这些变形效果很大程度上依赖于材料的本构模型[1]，即可以用来表述形变体材料中的应力与应变之间的函数关系。文献[2]列出了几种比较常见的本构模型，比如：线性模型、共旋线性模型以及非线性模型等。有了这些材料模型之后，我们可以进一步进行深入研究，尝试调节材料的一些相关参数来设计出一些不同的形变体。但是仅通过调这些参数来得到更加真实的形变效果是很困难的。事实上，这些特殊的标准材料是整个各向同性材料空间的一小部分，而且整个各向异性材料空间更加广泛。

为了获得更加丰富有趣的形变体形变效果，一些方法已经被提出。作为连续介质力学的基本方程，本构方程表示了一种给定材料的物理特性，这其中包括它引起的与之相关的材料变形反应(例如力、应力、能量)[3-5]。然而，这些方法由于Valanis-Landel应变能密度模型的限制，都是集中在类橡胶材料或者肌肉材料之上。在之后的研究工作中，文献[6]改进了Valanis-Landel应变能密度函数模型。基于此模型，本文提出了稳定的带约束的超弹性材料设计方法。但是与文献[6]不同的是：本文更关注稳定的材料编辑。

材料编辑的一个主要困难是如何编辑稳定的材料，因为无效的材料会导致仿真不稳定。因此，本文给出设计正交各向异性材料的稳定性条件，并详细讨论条件。设计稳定的各向异性材料比较困难，故提出了一种创新的各向异性材料能量，基于这种能量模型，可以很容易地设计具有稳定性和明显各向异性的各向异性材料。

1 相关工作

形变体仿真在计算机图形学领域当中一直是一个相当重要的研究课题。几种基于物理的方法被用于变形固体的仿真[7]，其中有限元方法被广泛使用。文献[2]详细介绍了经典的有限元方法，其中最基本的有限元方法模型是线弹性有限元模型。该模型很容易设计出来，因此广泛应用于计算机图形学领域的初期仿真。考虑到线性有限元模型在仿真过程中是用柯西小应变来度量形变，因此导致该模型仅适用于弹性体的小变形仿真。在很多形变情况下，弹性体较大的形变都是由于旋转导致的，因此文献[8]提出了共旋线性有限元模型，通过极分解，将弹性体局部旋转独立出来。然而，当弹性体处于较大拉力或者压力作用从而产生了较大拉伸形变时，共旋线性有限元仍然不能正确处理大形变，解决该问题的一种常见方法是使用二次的格林应变，也就是非线性有限元模型。文献[9]讲述了几种比较常见的非线性有限元模型。文献[10]在布料动画仿真中第一次使用非线性有限元方法。对于形变体，特别是对于软物质的形变仿真，在形变过程中单元很可能发生翻转的情况。然而单元的翻转通常是一种不正确的状态，应力计算常常会导致计算有误。文献[11]针对该问题进行了深入研究，最终提出了一种可翻转有限元方法，用以处理那些在仿真时出现翻转的单元。文献[12]使用隐式时间积分格式在可翻转有限元方法中求解形变静态平衡位置，同时为了使仿真稳定以及满足刚度矩阵是正定的，进一步修改了牛顿-拉夫森迭代算法。基于文献[11-12]，一些学者提出了多种改进效率的方法，比如降维仿真[13]、材料粗糙化[14]、多重网格法[15]等，这些方法几乎都是在形变不变量空间下进行计算。本文使用的有限元模型是在形变拉伸空间下进行仿真。

很多学者一直以来专心于研究有关各向异性材料方面的问题，例如：文献[16]介绍了横向各向同性超弹性材料,即形变体在垂直轴线的任一方向上所表现出来的性质是相同的。在非线性有限元方法的基础之上，文献[17]提出了一种横向各向同性材料的算法。文献[18]为了使横向各向同性材料在仿真过程中变得更加快速，在GPU上完成了有关形变体仿真算法的研究。文献[11]研究了怎样能够在横向各向同性材料中应用可翻转有限元模型。之前的仿真大部分集中于各向同性材料，文献[19-20]借鉴了在工程力学中用来编辑正交各向异性材料的相关思想，深入研究材料的相关性质以及限制一些物理参数，最终让仿真出来的形变体能够很好的保持稳定性，并在此基础之上，研究出了适用于一般线性各向异性材料的相关稳定性条件。本文与文献[19-20]的目标都是设计稳定的材料，但不同的是，本文的目的是设计非线性材料。

材料设计是一个有趣的热门研究课题,多样的真实的弹性体材料一直为研究学者所追求。目前为止已经提出了很多种关于材料设计的方法。在工程物理学科中，基于物理的材料编辑方法(physically-based modeling method)最为常见。该方法是通过直接设计材料的本构函数，并调整参数，使得本构函数曲线拟合实验数据。由于文献[21]提出的应变能密度函数模型是分离形势的，而且数学推导很严格，物理解释也很直观，因此该模型被研究学者用来预测形变特征[22-24]。之后文献[5]在文献[21]的基础之上，展开了对不可压缩的各向同性形变体的研究。而针对有关各向异性材料的编辑方法，文献[3-4]则重点进行了一番研究。其中，文献[3]在其函数模型中通过添加各向异性项部分，提出了适合各向异性材料的函数模型。文献[25]在计算机图形学领域中第一次将基于物理的材料设计方法引入进来，之后多个研究工作在其基础之上进行展开。如设计人体躯干方面的本构模型[26]、设计手部手指方面的本构模型[28]、设计人脸方面的本构模型[27]等，但是这些研究进展都是针对某一特定类型的材料，并不适用于一般性的材料设计。针对此种情况，文献[6]运用和文献[5]相似的思路，在设计材料的应变能密度函数的时候参考了文献[21]的模型来编辑更加普遍的材料。虽然我们可以基于能量模型和文献[6]的样条插值方法上设计新的材料，但是设计出的材料往往仿真不稳定，会出现固体膨胀、收缩等错误。仔细的设计可以避免这些问题，但是就会显得不方便。所以本文详细讨论了如何更加稳定地设计材料并且更加方便地展示了稳定性条件。除了基于物理的建模方法，我们注意到基于数据驱动的材料设计方法[29-31]和基于测量的建模方法[32-34]已经在图形学方法中大受欢迎，因为它们可以产生非常逼真的模拟。

2 可分离的应变能密度函数

应变能密度函数用来表述给定材料的物理特性。通过设计应变能密度函数可以模拟出新的材料。然而，整个应变能密度函数的空间是很大的，研究这个空间不是很容易。

2.1 应变能密度函数

基于Valanis-Landel应变能模型[21],本文把应变能密度函数ψ作为λ1、λ2和λ3的函数,λi是变形梯度F的奇异值，也表示沿着主轴捕捉变形的主拉伸。此外，对于各向同性材料，它们在任何方向上都有相同的特性。所以应变能密度函数ψ(λ1，λ2，λ3)应该满足对称性的性质：

ψ(λ1，λ2，λ3)=ψ(λi1，λi2，λi3)

(1)

式中：i1、i2、i3是(1,2,3)的排列。但在为各向同性材料建模的时候，很难以满足对称性的要求。为了克服ψ的对称性,文献[6]扩展了Valanis-Landel可分离应变能量密度函数,它采取的形式是:

ψ(λ1，λ2，λ3)=f(λ1)+f(λ2)+f(λ3)+g(λ1λ2)+

g(λ1λ3)+g(λ2λ3)+h(λ1λ2λ3)

(2)

式中：f、g、h是一维非线性的标量能量密度函数，分别表示单轴(长度)、双轴(面积)和三轴(体积)应变。与Valanis-Landel可分离的应变能密度函数不同的是，Valanis-Landel抛弃了g和h,这是因为其着手于橡胶材料g=0以及不可压缩材料h=0。由于f是与材料变形的拉伸有关，h是与体积有关，所以本文集中于编辑橡胶材料h=0。当设计正交各向异性形变体时，其中的各向同性部分只需要设计f和h。另外为了保证ψ的对称性，这种分离的形式使材料模型编辑更加简单和直观。

2.2 基于拉伸的仿真

之前的有限元模拟方法大多数集中于不变量空间，即ψ(I1,I2,I3)，比如可翻转有限元法求解大变形[8]，然而我们的能量模型需要仿真拉伸空间ψ(λ1,λ2,λ3)。

(1) 有限元力的计算。根据可翻转有限元的工作[8]，首先由式(1)计算各项同性得第一类Piola-Kirchhoff应力,然后使用可分离的应变能模型计算：

(3)

(4)

λ2λ3h′(λ1λ2λ3)

(5)

计算内力为:

式中：W是四面体的体积,Dm是参考形状矩阵。由于W和Dm在仿真中保持不变，可以预先计算并存储它们。

(2) 单元刚度矩阵的计算。整体刚度矩阵是通过单元刚度矩阵集成获得的，对于每一个形变体中的四面体单元，通常把单元刚度矩阵K定义为：

(6)

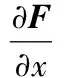
(7)

2.3 超弹性材料的稳定性条件

基于分离应变能函数，用户能够方便地设计新的材料模型。然而，随意设计函数可能会导致模拟不稳定。本文首先总结出了一些关于设计应变能密度函数模型的稳定性条件；然后描述了怎样满足这些条件来方便和友好地设计材料；最后讨论了设计正交各向异性材料的方法。

为了能够设计出稳定的正交各向异性形变体的应变能密度函数ψ，其应该满足以下约束条件：

(1)ψ是一个非负函数。

(2) 在形变体未形变状态下,即λ1=λ2=λ3=1,ψ取得函数最小值且最小值为0,这个条件能够保证形变体在未发生形变状态下的势能为0,内部无弹力。

(3)ψ是一个凹函数，也就是形变体形变越大，其势能越大,内部弹力越大，并且这一条件保证了最终计算的刚度矩阵正定，使得仿真计算稳定[2]。

(4) 在形变体极限形变状态下，即λi=0或者λi=∞，ψ的值趋于正无穷。或者说，当λi=0时，形变体内部弹力趋于负无穷，而当λi=∞时，形变体内部弹力趋于正无穷。即：

(8)

(9)

(10)

(11)

根据这些稳定性条件，我们可以更好地仿真正交各向异性材料。

3 可正交各向异性材料的编辑

各向异性材料在不同的方向上表现出来的特性是不同的，这与各向同性材料有显著的区别。由于各向异性材料具有巨大的材料空间和复杂性，设计出合理的本构模型实属不易。而正交各向异性材料相比之下就要容易一些，该材料往往会在三个正交方向上(称为材料方向m1,m2,m3)展现出不同的刚性特性，并有广泛的应用。文献[6]提出了有关正交各向异性材料的分离应变能模型。基于这种能量模型，可以对正交各向异性材料进行建模，但是它很难保持材料稳定，即满足材料稳定条件。为了设计出更加稳定的正交各向异性形变体模型，我们在文献[6]的基础之上改进了正交各向异性材料的可分离应变能模型。

ψ=ψiso+ψortho

(12)

(13)

(14)

其中，应变能密度函数ψ包括两部分：一部分是各向同性能量项，其表现的是各向同性形变体的物理性质；另外一部分则是正交各向异性能量项，其反映的是材料的正交性质。因为稳定性条件(1)要求所有的应变能密度函数ψ都为非负函数，所以可以简单地使式(12)中的所有各向同性能量项ψiso和各向异性能量项ψortho满足稳定条件，从而设计出一个稳定的正交各向异性材料。

3.1 各项同性能量项部分的设计

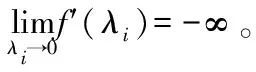
3.2 各项异性能量项部分的设计

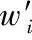
(15)

因为：

(16)

所以：

(17)

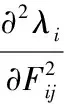
(18)

(19)

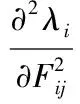
(20)

(21)

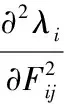
(22)

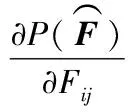
(23)

(24)

(25)

式中：Fi,j表示第j行等于F的第i行、其他位置都为0的矩阵。

4 实 验

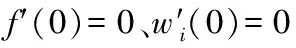
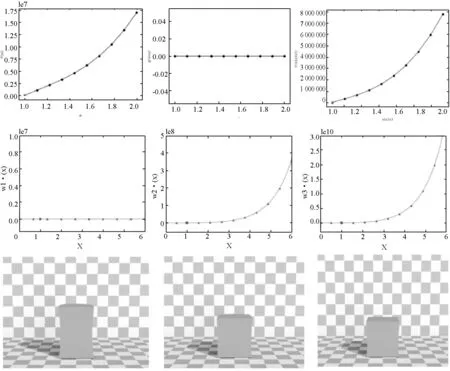
图1 稳定的cube模型的设计

(a) 本文设计的材料模型(b) stvk材料模型 (c) Neohookean材料模型图2 形变体turtle对比实验

本文通过对比实验来说明材料稳定性条件的必要性,以及用本文方法编辑bar模型时的有效性。不稳定的bar模型如图3所示(973个顶点,2 912个四面体)。固定bar的顶部除了重力之外没有任何外力负载。在这组对比示例中,每个示例的曲线g′和h′都是相同的并满足条件,材料a满足所有条件，材料b和c不满足条件(2)，材料d不满足条件(3)。调整f′故意打破能量最小条件(条件(2))和能量凹性条件(条件(3))。应变能密度函数在满足能量最小条件和能量凹性条件的情况下是被认可的。而且,即使bar模型经历大变形，如图4所示，材料建模方法也很稳健。

(a) (b)

(c) (d)图3 不稳定的bar模型(时间步长为0.001)

图4 bar模型的扭曲(时间步长为0.001)

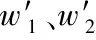
(a) 本文正交异性模型(b) 各向同性模型(c) 共旋线性正交异性模型图5 形变体cube模型对比实验

为了说明材料的正交各向异性,分别在立方体的m1、m2、m3方向上应用初始位移。与各向同性材料和旋转线性正交各向异性材料比较最大拉伸位置时的状态,本文的材料确实表现出非常明显的正交异性特性,它分别在m1、m2、m3方向显示出不同的刚度。正交异性dragon(5 803顶点,20 140个四面体)也表现出了良好的稳定性和明显的正交各向异性，如图6所示。

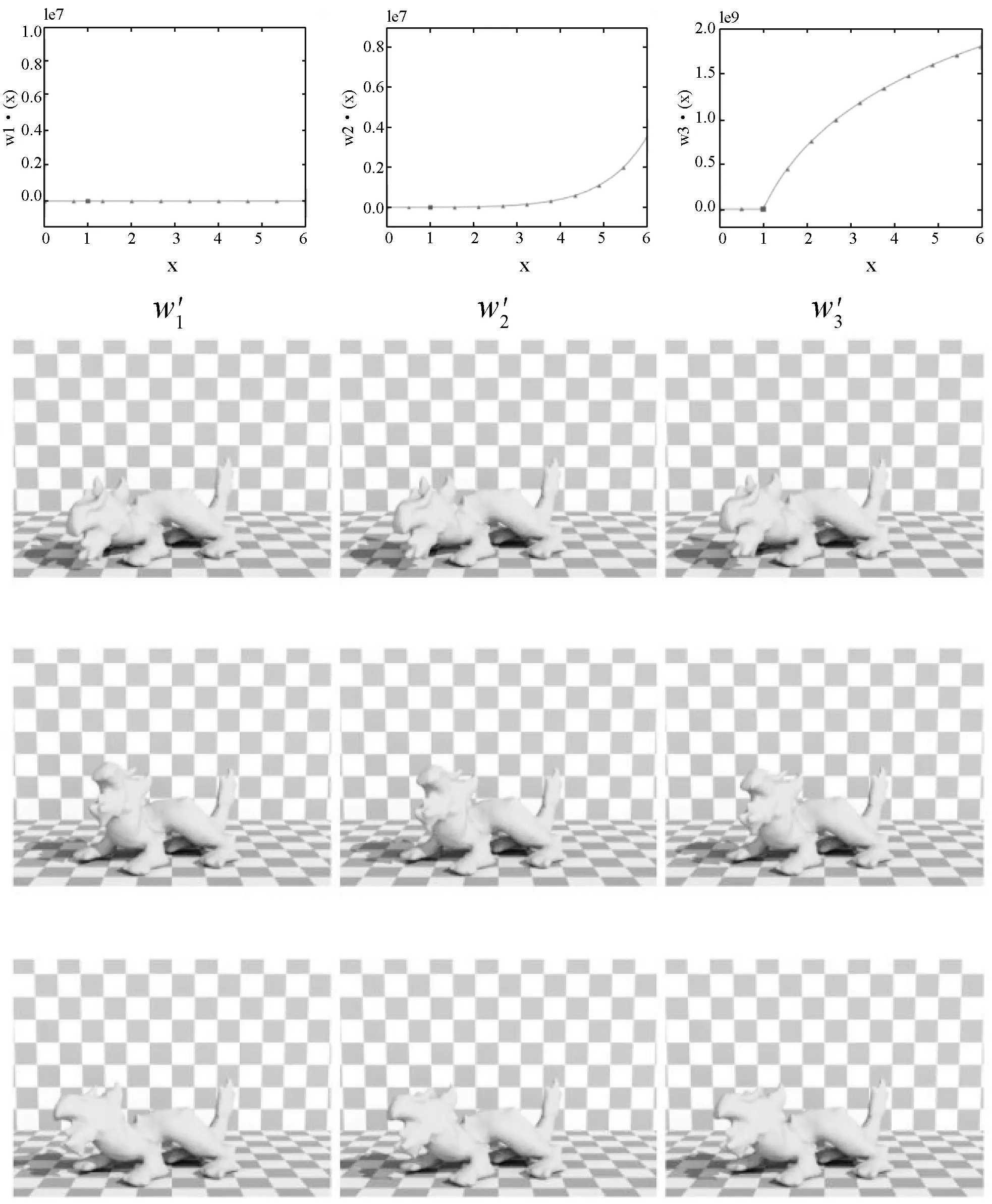
(a) 各向同性模型(b) 本文正交异性模型(c) 共旋线性正交异性模型图6 形变体dragon模型对比实验

在与各向同性材料的对比实验当中，设置了一样的杨氏模量Eiso和泊松比v。在仿真旋转正交异性恐龙时,E1=Eiso,E2=0.1×Eiso,E3=100×Eiso。与正交各向异性cube模型的例子不同的是,我们分别在x、y和z方向上应用初始力而不是初始移位。

此外，本文的非线性正交各向异性和旋转线性正交各向异性立方体几乎在相同的时间步时长达到最大拉伸位置。但是,非线性正交各向异性立方体在第57时间步到达最压缩位置,而旋转的线性正交各向异性立方体到达该位置在第36个时间步长，如图7所示。

(a) 非线性正交异性模型(b)旋转线性正交异性模型图7 形变体达到最压缩位置时的对比实验

5 结 语

为了模拟稳定材料保证材料的稳定性,本文围绕材料的稳定性条件进行详细讨论，并提出了一种更加方便和直观的材料建模方法。同时，展示了一个正交异性材料模型,可用来设计具有稳定性以及明显的正交各向异性特性的正交各向异性材料。本文改进了正交各向异性的可分离应变能模型材料中的应变能密度函数,在此函数模型中重点研究了正交各向异性能项。为了避免计算各向异性形变体仿真的复杂性，本文主要针对的是正交各向异性形变体的仿真，所以今后将探索更加方便和直观的方法来设计一般化的各向异性形变体仿真。