基于蜂拥的智能电网动力学模型分析与控制

陈世明 武 鹏

(华东交通大学电气与自动化工程学院 江西 南昌 330013)

0 引 言

电网建设随着用户电力需求的日趋增长而不断扩大，在可持续发展政策的推进及市场环境自由化趋势下，电网公司不断调整运行方案以适应外部条件从而使得电网的物理特征表现出更强的非线性。智能电网作为推动产业革命实现绿色发展的新动力，旨在提高系统各部分运行效率、降低成本和环境影响，并尽可能提高系统可靠性与供电质量[1-2]。智能电网的不断发展使得本来就已经很庞大的电力网络又结合了先进的信息网络，电网的安全稳定运行控制变得越来越复杂，引发了发输变配用各方面的全面革新，迫切需要具有智能电网学科知识支撑的、强有力的基本模型来有效地帮助理解智能电网信息-物理网络间交互关系[3-4]。文献[5]考虑了关于智能电网信息物理网络的一些经验模型，但其存在着过于简化的单一发电机与负荷相连的建模方法。文献[6]依据基尔霍夫定律从复杂网络点与边抽象关系的角度探究电网的稳定性问题。文献[7]则进一步考虑了智能电网信息、物理相依网络的耦合度对电网稳定的影响。有学者在网络科学中找到了更符合实际的模型与动力学表达之间的联系[8-10]。本文依据物理电网动力学模型[10]并借助用于对大规模自然现象建模的群体智能的思想，融合了信息智能与控制行为。

智能电网中信息网络结合了基于PMU的广域测量[11]，相较传统集中式电网控制中心与监控与数据采集(SCADA)之间信息传输，广域测量灵活、高效的特点更适于智能电网信息-物理网络交互。物理网络结合了电网暂态稳定、互联摇摆方程及多智能体智能电网等方面的工作[12-15]，把协同控制策略应用于融合信息网络的物理电网中。本文将信息网络动力学融入所研究的问题中，使得信息-物理依赖性特征表述在智能电网研究中更为突出。通过引入多智能体框架并在由暂态稳定要求的约束条件下，建立起智能电网信息-物理网络间的交互模型。然后将所提出的基于蜂拥的信息-物理控制器应用于模型，并根据李雅普诺夫理论证明了其稳定性。最后通过仿真分析，验证了多智能体框架内蜂拥控制的有效性。

1 基于多智能体系统的网络化框架

1.1 智能电网信息-物理网络融合

多智能体网络化动力学系统模型如图1所示， 3机9节点WECC系统及其他更大系统都是这类融合信息和物理元件的综合系统。本文建立的模型由信息-物理智能体组成，每个智能体包含：(1) 一个表示物理电力网络元件(如发电机等)的动态节点；(2) 一个相量测量单元(PMU)，从动态节点及其关联活动节点获取物理数据如功角和频率等；(3) 一个本地信息控制器，它从PMU获取数据来计算控制信号并输出到发电机节点。由于本地控制器和PMU有数据采集、通信和计算的任务，统一被视为信息元件。

图1 多智能体网络化动力学系统等效模型

本文的重点是研究智能电网暂态稳定问题，本地控制器的目的是在系统受到信息-物理扰动后实现系统内发电机的频率同步。每个智能体都会配备各种类型的电源诸如电池、插电式混合动力新能源汽车(PHEVS)以及飞轮等储能设备，使本地控制器快速动作以达到整个电网中发电机同步的目的。PMU可通过数据集中器PDC间接相互通信，使所有智能体都可以访问信息并做出有效的控制决策，不会改变多智能体框架。多智能体等效模型同时也考虑了有效数据(信息)流和电力(物理)潮流。

1.2 智能电网多智能体动力学及交互

假设有F个智能体，每个智能体都有描述信息-物理交互的耦合动力学系统方程。为描述物理网络，利用简化的摇摆方程为每个智能体给出[16]：

(1)

通过向描述物理网络的互联摇摆方程添加控制输入，包含PMU信息和本地控制器的信息网络与物理网络构成多智能体框架，得到：

(2)

式中：ui=Pu,i是第i个智能体的控制输入，并由从系统中所有PMU获得的数据(θi(k)和ωi(k)，i=1,2，…,F，k为时间常数)经函数计算得出。控制输入可以被理解为由快速作用外部电源向相应发电机节点上注入功率为正Pu,i或者吸收功率为负Pu,i，也可以认为是将有关ui的计算转换为有功功率的信息-物理连接。

测量设备测得物理信息如功角和频率等作为PMU数据，信息到物理的连接便产生于测量设备。式(2)动力学表示信息-物理交互关系，当计算的信息网络控制输入ui应用(通过注入功率Pu,i)到发电机所在电力网络中时，就形成了信息网络到物理网络的连接。控制输入ui建模为PMU数据的函数，能够表示信息网络对整个多智能体框架影响。对于正常系统运行来说，ui=0，系统受到扰动时，ui会激发系统重新实现暂态稳定，ui的计算依赖于系统中相应控制器的期望值。

1.3 智能电网暂态稳定问题描述

本文侧重于对实现暂态稳定的控制器进行设计同时完成对信息网络动力学建模。暂态稳定描述了电力网络在受到大干扰(例如输电线路故障和发电机损耗等)时保持同步的能力。在一个受故障的系统中要合理地应用控制策略实现暂态稳定，就需要满足包括保持频率同步和功角聚合的要求。频率同步要求所有发电机的频率一致渐近于一个共同值f0,通常设定为60 Hz,归一化为1。功角聚合要求每个发电机的功角和惯性中心(COI)相位角之差应低于一个预定义阈值(通常选为5π/9)。

经过分析后列出如下暂态稳定目标要求：

1) 频率同步：

ωi(t)→1(t→∞)

(3)

式中：ωi(t)为发电机i在时间t时的归一化频率。

2) 功角聚合：

|θi(t)-θCOI(t)|≤γ∀t

(4)

式中：γ实际上通常设置为5π/9；θCOI(t)是COI相位角定义为：

(5)

由式(4)和式(5)可以得出功角聚合的充分条件为：

|θi-θj|≤5π/9i,j∈V,V={1,2,…,F}

(6)

2 基于蜂拥的智能电网动力学模型分析与控制

2.1 智能电网信息-物理网络交互模型

式(2)中智能体间信息耦合和物理耦合关系描述如下：

(7)

图1所示的智能电网多智能体网络化等效模型显示了信息节点到物理节点一对一紧密耦合关系，符合实际电网状况。若要实现信息网络对物理网络的有效影响就要对信息网络控制输入ui进行合理设计。由此对式(7)中的物理量做出如下两个假设：1) 假设对于每个智能体ui=Pu,i的变化率远远大于机械输入功率Pm,i并且电网恢复暂态稳定的时间较短，这时就可将Pm,i视为常数；2) 假设电压调节问题与暂态稳定问题是解耦的，这使得在控制器激活以重新实现系统暂态稳定时，电压Ei可被视为常数。

在上述假设下，对式(2)两边求导,依据多智能体二阶动力学模型可改写系统动力学为[17]：

(8)

(9)

式中：bij是奇异摄动分析参数；gij>0是控制参数；Ni表示第i个智能体的邻居集合；h(·):RF×RF→R是向量θ=[θ1,θ2,…,θF]和向量ω=[ω1,ω2,…,ωF]的一个函数。

把式(9)代入式(8)的第二行得到：

(10)

此时可以利用奇异摄动分析式(8)中动力学，将式(8)以向量形式表示：

(11)

式中：M=DΨ；Ψ=(I+B)；I是一个单位矩阵；D=diag[D1,D2，…，DF]；B=[bij]以及G=[gij]均为F×F信息控制矩阵；L是一个F×F物理耦合矩阵，其中的元素可表示为：

(12)

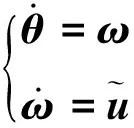
(13)

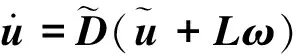
(14)

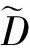
2.2 类比蜂拥的控制器设计

(15)

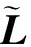
1) 势能函数：基于式(6)的充分条件，考虑下列势能式：

(16)

式中：ψ(·)是表述为智能体间引力势,定义为：

(17)

(18)

其中：

(19)

3) 信息控制矩阵B：信息控制矩阵B的作用是保证存在有效的奇异摄动参数，对信息控制矩阵B有如下附加约束：

(20)

5) 功率Pu,i：由上分析推导得到发电机注入功率Pu,i的相关结果有：

(21)

式中：c2=1，对式(21)两边积分，得到外部电源与同步发电机之间的传输功率Pu为：

(22)

2.3 智能电网信息-物理网络动力学稳定性分析

定理：考虑由式(13)与式(15)构成的二阶系统，假设发电机间保持通信且初始能量H0为有限值，则在蜂拥控制式(15)的作用下所有智能体的动态参数都会收敛到如式(3)、式(6)描述的稳定条件下，最终实现智能电网的稳定运行。

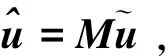
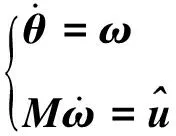
(23)

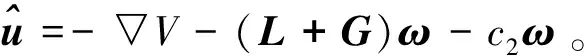
定义如下李雅普诺夫函数：

(24)

显然对∀(θ,ω)≠(0，0)，有H(0，0)=0且H(θ,ω)>0。根据式(11)导出的动力学计算H的导数，得到：

-ωT(L+G+c2I)ω

(25)

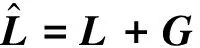
3 仿真与分析

本文采用MATLAB/Simulink进行仿真验证，如图2所示3机9节点WECC系统研究结果显示了本文基于蜂拥的控制结构实现暂态稳定的性能。以发生故障及故障后加入控制的情况作为研究，将9节点电网模型的线路4-5和节点6以受扰位置分为三个实例进行分析。在给出的三个实例中假定在t=0 s时发生三相短路故障，t=0.3 s时断开故障线路，并于t=0.4 s时激活控制器并确定输入ui=Pu,i，所有发电机物理量的仿真观察时间均为8 s。

图2 WECC 9节点电网模型

实例1：

线路4-5发生三相短路故障，三台发电机转速、功角差随时间变化分别如图3、图4所示。8秒时间区间内不施加任何控制，即未激活实现智能电网信息物理交互的控制器，电网不稳定性显而易见，转速波动大、功角差大于5π/9。若在t=0.4 s激活基于一致性控制后，发电机各物理量分别如图5、图6所示，转速、功角差值经过一段时间的波动后处于稳定范围内，系统经过控制恢复到稳定状态所需的时间较长。若在t=0.4 s激活基于蜂拥控制后，发电机各物理量分别如图7、图8所示，系统快速恢复到稳定状态，转速平稳且功角差值处于稳定范围内。

图3 实例1中不施加任何控制的发电机归一化转速

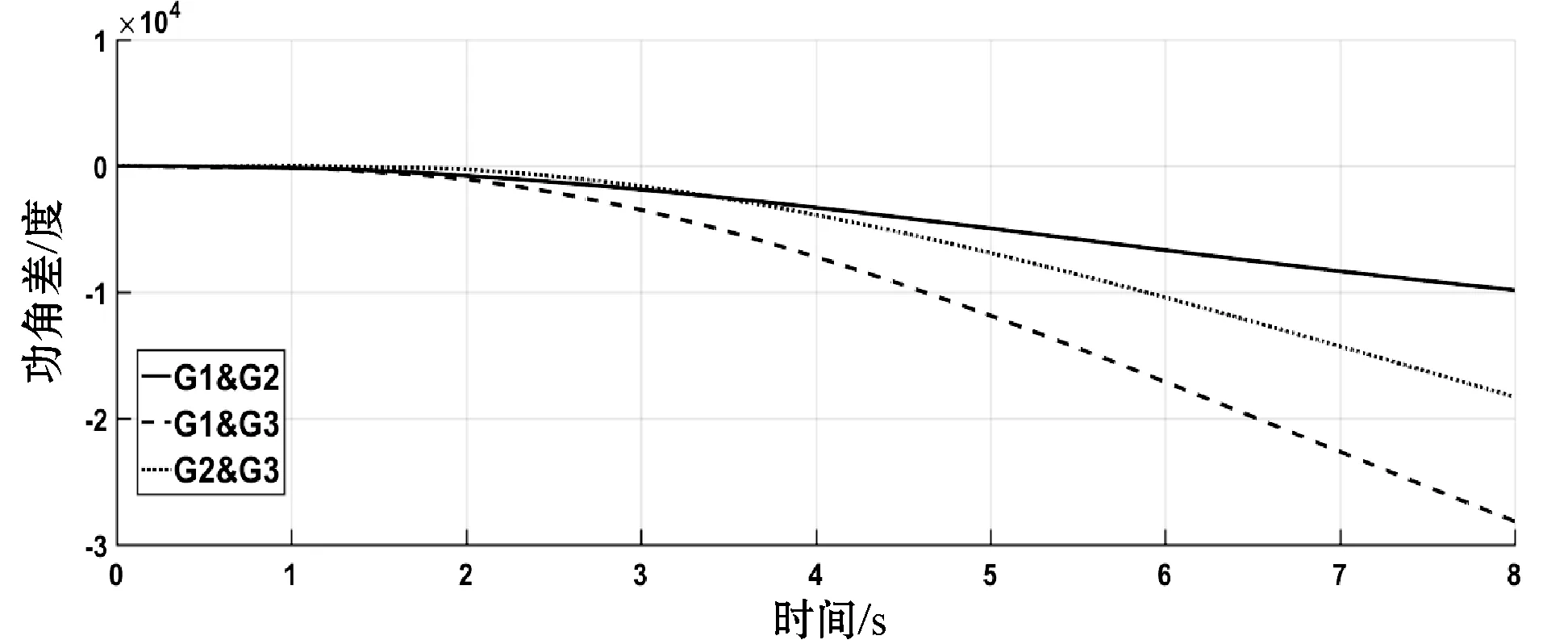
图4 实例1中不施加任何控制的发电机功角差

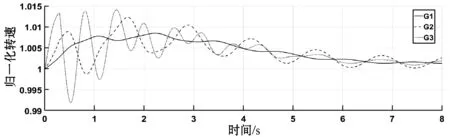
图5 实例1中施加一致性控制方法的发电机归一化转速

图6 实例1中施加一致性控制方法的发电机功角差

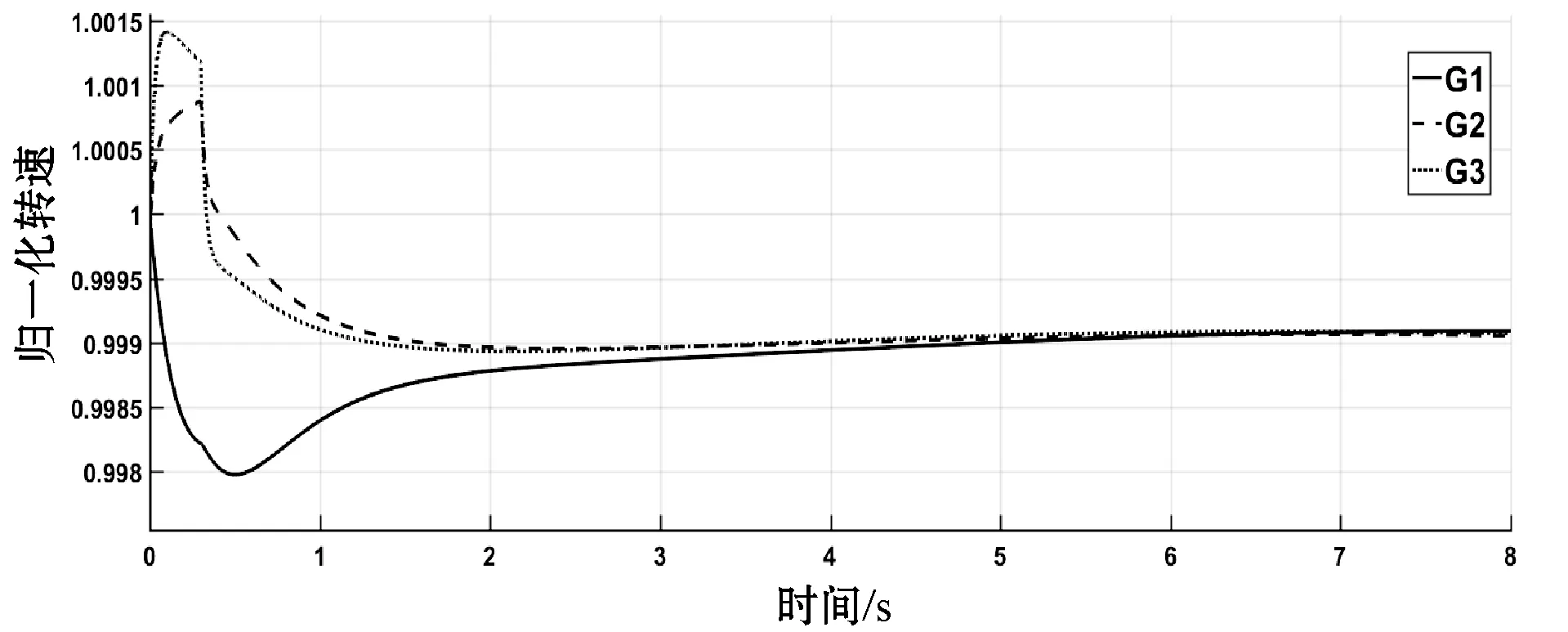
图7 实例1中施加本文控制方法的发电机归一化转速

图8 实例1中施加本文控制方法的发电机功角差

实例2：

节点6发生三相短路故障，三台发电机无控制8秒内的转速、功角差随时间变化分别如图9、图10所示，即该时间区间内未激活连接信息-物理网络的控制器，电网显然处于不稳定状态，功角差大于5π/9。若在t=0.4 s激活基于一致性控制后，发电机各物理量分别如图11、图12所示，转速、功角差值经过一段时间的波动后处于稳定范围内，系统经过控制恢复到稳定状态所需的时间较长。若在t=0.4 s激活基于蜂拥控制后发电机各物理量分别如图13、图14所示，控制后转速更快趋于平稳、功角差值处于稳定范围内，系统快速恢复到稳定状态。

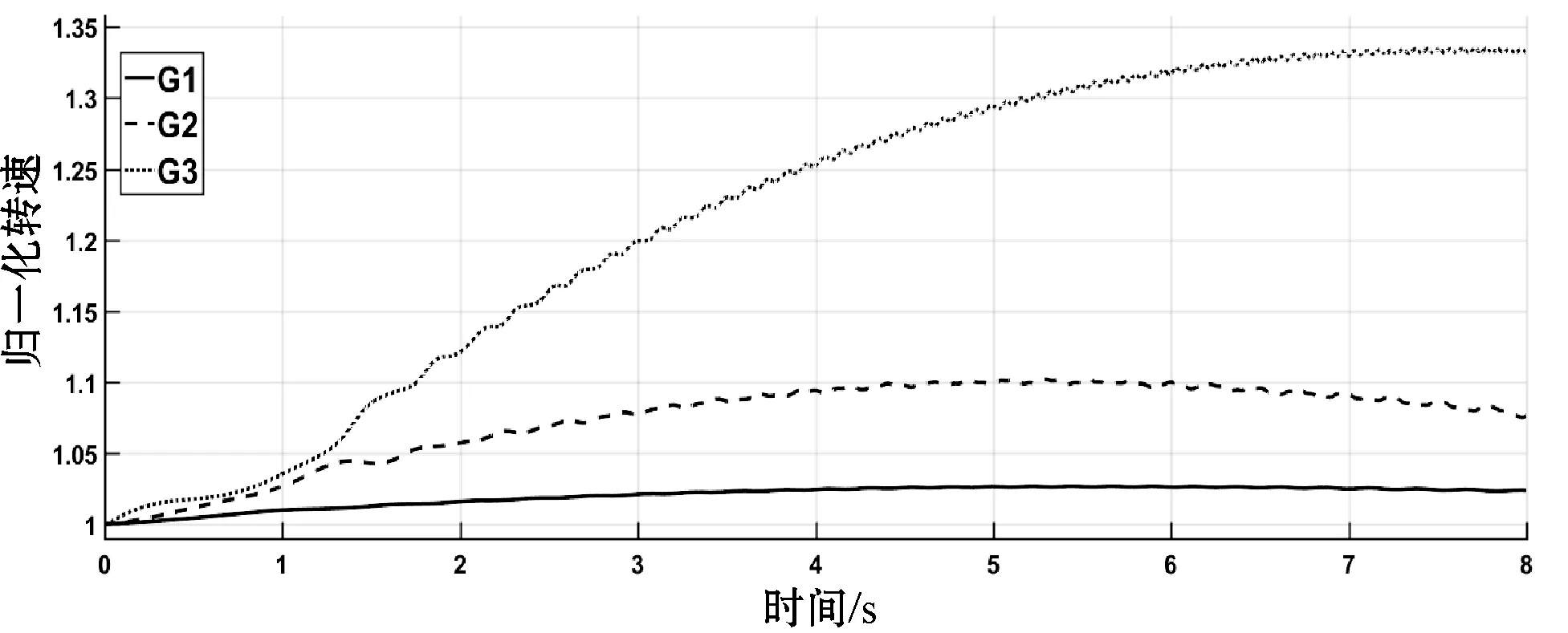
图9 实例2中不施加任何控制的发电机归一化转速

图10 实例2中不施加任何控制的发电机功角差

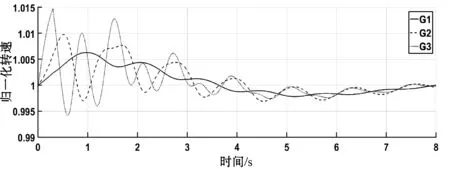
图11 实例2中施加一致性控制方法的发电机归一化转速

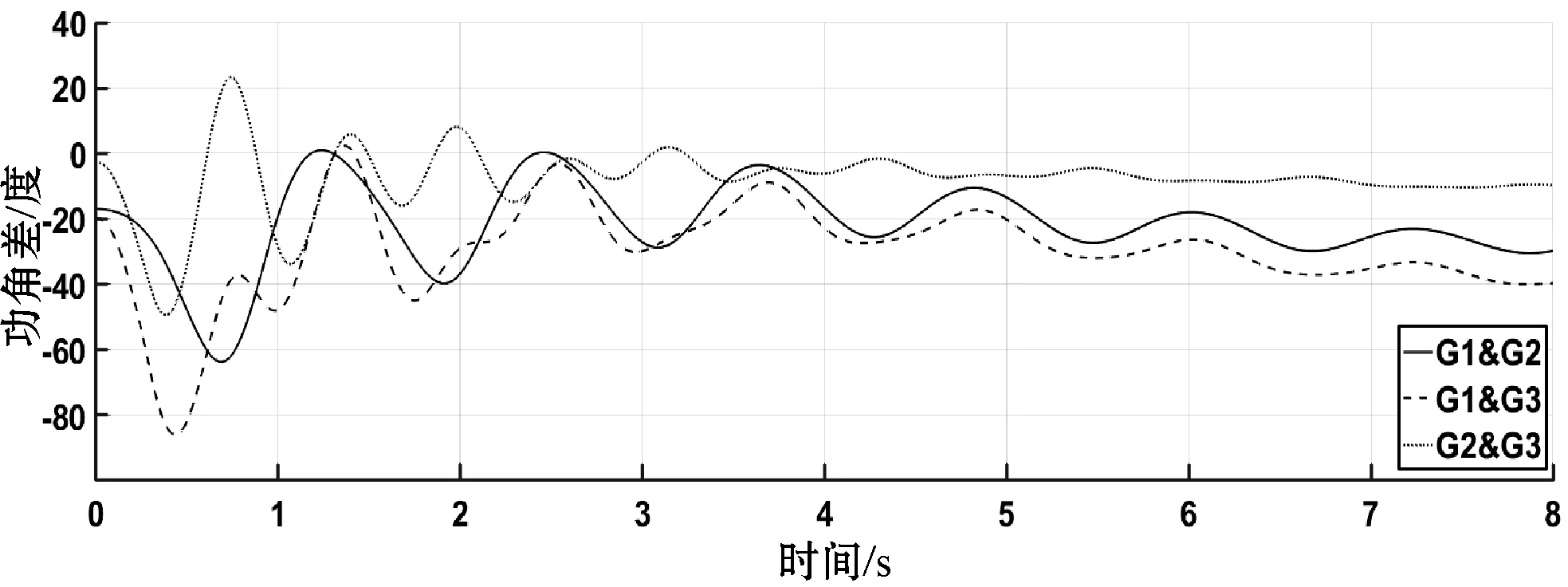
图12 实例2中施加一致性控制方法的发电机功角差

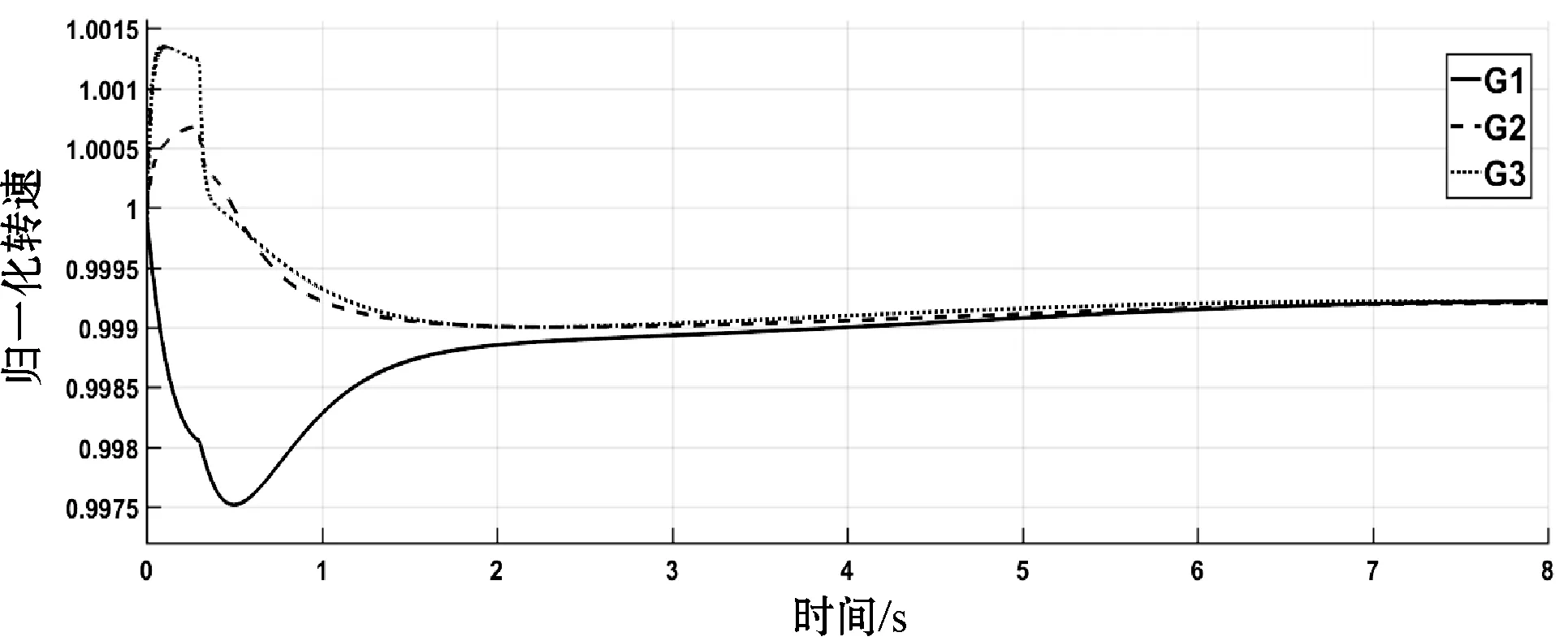
图13 实例2中施加本文控制的发电机归一化转速

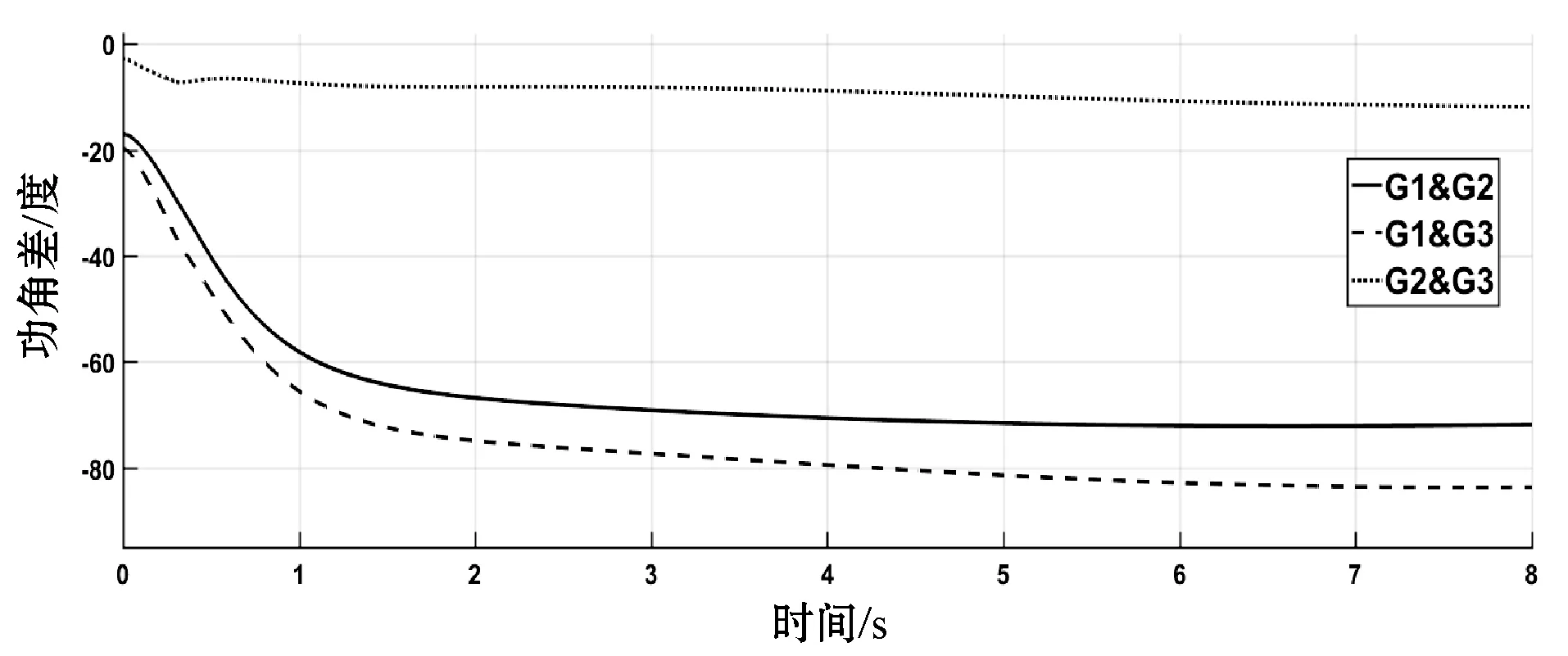
图14 实例2中施加本文控制的发电机功角差

4 结 语

本文研究了基于蜂拥的多智能体动力学系统框架，并对有关暂态稳定问题的智能电网信息-物理交互关系模型进行了分析与控制，其中每个智能体都包含相应的同步发电机、PMU和本地控制器，外部快速反应的电源为实现暂态稳定应用了功率控制。本文阐述了在各智能体动力学方程中合理描述信息与物理耦合的方案，使物理电网动力学模型与信息(通信与控制)网络的融合更加简单有效。仿真结果显示了应用蜂拥控制有更好的性能表现。之后的工作可利用信息网络动力学模型进一步对智能电网高效的分布式通信与控制策略深入探索。