综合与实践活动：《摆一摆，想一想》教学设计

王丽君

【中图分类号】G642.4       【文献标识码】A

【文章编号】2095-3089（2019）23-0298-01

教学内容：人教版数学一年级下册第四单元第51页“摆一摆，想一想”

教学目标：

1.通过把一定数量的圆片分别摆在数位表上不同的位置得到不同的数的活动，加深100以内的数的认识，进一步巩固数位与数值的概念。

2.经历观察、操作、比较、猜想、验证、归纳等学习数学的过程中感悟100以内数的特点及排列规律，并能用发现的规律解决一些简单的数学问题，感受数学思考过程合理性的同时，初步培养学生的有序思考的能力和抽象概括能力。

3.在合作交流中养成倾听，有条理表达想法的习惯和能力，帮助学生学会学习、学会思考，感受到数学的奥妙，富有趣味性，从而激发学生热爱数学的兴趣。

教学重点：在摆数的过程中感悟位值思想。

教学难点：在活动中感受有序思考的价值。

教学准备：教具：数位表、汇总表、磁性圆片20个、课件。

学具：数位表、记录单、纸质圆片20个。

教学过程：

一、谈话激趣，揭示课题

师（板书1、10）：这是几和几？

生：是1和10。

师：老师手里有1个圆片，你们能不能用这一个圆片分别表示出1和10呢？

生：能表示出1，不能表示出10。

师：如果老师给你们一个数位顺序表，（出示数位表，并贴在黑板上）现在能用这个圆片分别表示出1和10吗？

生：能！（学生在数位顺序表上摆圆片。）

师：同样是1个圆片，为什么表示的数不一样？

生：它摆放的数位不同。放在个位上表示1个一，放在十位上表示1个十。

小结：把1个圆片放在不同的数位上就能表示不同的数。如果有更多的圆片，又能表示多少个不同的数呢？这节课，我们就一起“摆一摆，想一想”（板书课题），从中探索有趣的数学知识吧！

【设计意图：通过对1和10这两个最简单的数的认识，同时又复习了数值和数位，降低了学习的难度，也激发了学生的学习兴趣，新知的学习也在不知不觉中得到了渗透。】

二、独立操作，感知有序性

1.学生试摆。

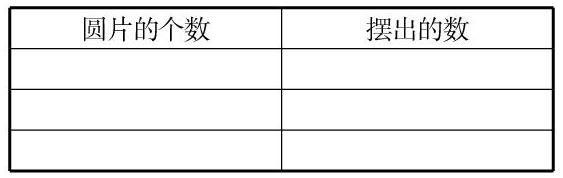
师：刚才我们用1个圆片在不同的数位上摆出了1和10（出示汇总表，把1和10写在汇总表上），下面请同学们拿出2个圆片，试着在数位表上摆一摆，并且把摆出的数填在记录单上。

圆片的个数摆出的数

2.交流摆法。

预设一：生1：我摆出了2、20、11三个数。

师：你是怎样摆的？

生1：我是先摆个位，把2个圆片都放到个位上得到数2，再把2个圆片都放到十位上得到数20，最后十位上放一个、个位上放一个，就得到数11。

师：请这位同学上台摆给大家看一看，一边摆，一边把摆的数记录下来。

师：看明白了吗？谁再来摆一摆？

师：还有不同摆法吗？

预设二：生2：我摆出了20、11、2三个数。

师：你是怎样摆的？上来摆给大家看看。

生2：我是先摆十位，把2个圆片都放到十位上得到数20，再从十位拿一个圆片放到个位就得到数11，再从十位拿一个放到个位就得到数2。（学生一边说一边摆。）

追问：这位同学是从哪位摆起的？

生：从十位摆起，然后一个一个的往个位上移。

师：还有没有不同的摆法？

预设三：生3：我摆了2，11，20三个数。

师：你是怎样摆的？上来摆给大家看看。

生3：我是先摆个位，把2个圆片放到个位上得到数2，又从个位拿一个放到十位得到数11，再从个位拿一个放到十位就得到20这个数。

追问：这位同学是从哪位摆起的？

生：从个位摆起，然后一个一个往十位上移。

3.小结摆法。

师：同学们，刚才这三种摆法，你最喜欢哪种？预设：生：喜欢第2种和第3种。师：为什么？生1：这两种方法都是先把圆片都放在十位或者个位，然后一个一个往另一位上移圆片，直到没有圆片为止。生2：他们是有顺序地摆的。师：是的，同学们观察可真仔细！这样摆就会让摆出来的数既不重复也不遗漏，要么从大到小排列，要么从小到大排列。

课件出示两种摆法，让学生加深印象。老师把摆出的3个数按顺序写在汇总表上。

【设计意图：感悟有序的思考方法是本节课的教学目标之一，也是教学难点。设计时我有意让学生多次演示摆的过程，多次指名让学生说一说摆的方法，然后又在课件上演示有序摆数的过程，目的在于强化有序思考，引导学生掌握有序思考的方法。】

三、合作體验，理解有序性

1.熟悉方法：用3个圆片摆数。

师：用3个圆片，与同桌合作摆一摆，看你能不能把所有的数都摆出来。要求左边的同学摆，右边的同学边看边在记录单上填写摆出的所有的数。

（摆完后请两组同桌到黑板上演示，讲述摆的方法，引导有序思考和有序摆的方法。老师把摆出的4个数写在汇总表上。）

2.巩固方法：用4个圆片摆数。

师：请同学们继续合作用4个圆片摆数。要求右边的同学摆，左边的同学边看边在报告单上填写摆出的所有的数。请一组学生把摆出的数写在汇总表上。

【设计意图：合作学习是一种很好的共同进步的模式，能促进学生间在学习上的互相帮助，共同提高。并且连续几次动手操作的安排，注重了学生动手和动脑密切结合，使学生的思维得到了锻炼，也为学生积累了数学活动经验。】

四、深入探索，发现规律

1.闭眼思考：用5个圆片摆数。

师：接下来，要提高难度了，同学们不准摆圆片，你能闭上眼睛和老师一起说出5个圆片可以摆出哪些数吗？

生：能！

师：请同学们闭上眼睛。老师现在把5个圆片全部摆在个位上，摆出的数是几？

生：5！

师：现在从个位移1个到十位，现在摆出的数是几？

生：14！

老师依次引导学生说出摆出的数：23、32、41、50。（老师记录在汇总表上）

追问：还有可以移动的圆片吗？

生：没有了。

师：那也就没有可以摆出的数了。请同学们睁开眼睛。

2.小结规律：用6个圆片摆数。

师：同学们，如果我们用6个圆片摆数，猜猜看，可以摆多少个数？

生：可以摆7个。

师：真的吗？那我们就试着把6个圆片在脑子里摆一摆，记一记，看是不是有7个？

生在记录单上记录，师巡视指导。

学生汇报记下的数：6，15，24，33，42，51，60。

师：真的有7个数呢！你们有什么发现？

生：摆出的数的个数比圆片数多1。

（课件出示：摆出的数的个数=圆片数+1）

师：我还想采访一下，你在十位上写2时，怎么这么肯定个位是4，而不是3，不是5？

生：因为有6个圆片，十位上用了2个，那个位上就只能用4个了。

师：那你们的意思是说，个位上的数字和十位上的数字加起来要等于圆片的个数，对吗？

生：对！

（课件出示：个位上的数字+十位上的数字=圆片的个数）

师：看来，用圆片摆数时不仅有一定的顺序，还有一些小秘密呢！

【设计意图：让学生闭上眼睛，暂时中断外界信息的干扰，可使大脑细胞的潜能最大限度地发挥作用，提高学生思维的深度和广度，同时也提高了学生的学习兴趣，为后面不摆圆片直接说出摆的数做好铺垫。】

五、运用规律，解决问题

1.下面的数是用几个圆片摆出来的？

81726354453627180

生：8個圆片！

师：你是怎么知道的？

生：因为2+6=8，3+5=8

师：也就是说每个数的个位上的数字和十位上的数字相加都得8，所以圆片有8个。

2.这里还缺了谁？你能补上吗？

18364572

师：你是怎么知道的？生：因为1+8=9，3+6=9，可以知道这是用9个圆片摆出的数，所以第一个从小到大排列应该是9，后面依次是27，54，63，81，90。

3.下面哪几个数不是7个圆片摆出来的？

716243543526170

生：24和35。师：为什么？生：因为2+4=6，3+5=8。师：怎么改正？生：应该是25，34。

【设计意图：让学生根据自己总结、归纳出的规律和方法来解决简单的问题，体现了由直观到抽象的层次，培养了学生的抽象思维。】

六、总结延伸，打破定势

师：通过这堂课的活动，老师相信你一定学到了不少知识，能跟大家说一说吗？

生1：我学会用一个或几个圆片摆出不同的数。

生2：我学会了摆数的时候要有顺序，才不会遗漏。

生3：我学会了摆数的时候要么从个位开始摆，要么从十位开始摆。

生4：我还学会了先从个位开始摆，然后逐渐向十位移动一个圆片。

……

师：同学们收获可真不少！请同学们继续思考：按照刚才的发现，10个圆片可以摆出几个数呢？

生：11个！

师：真的吗？我们可以怎样验证一下？

生：可以用圆片摆一摆，记一记。

师：你们又有什么重大发现？

生：用10个圆片不能摆11个数，只能摆9个！

师：同学们真了不起！那用11个圆片、12个……18个分别能摆出哪些数呢？是不是圆片越多摆出的数就越多呢？大家可以课余时间继续探讨。只要同学们认真观察，勤于动脑，善于思考，就会发现更多数学的奥秘呢！

【设计意图：让学生自己总结收获，加深印象，体验成功，也培养了学生归纳总结的能力。而后提出更高的要求，以供不同层次的学生进行知识的内化、升华。】