公路竖曲线计算程序的设计与实践

摘要：当汽车行驶在纵坡变坡点时，为了缓和因车辆动能变化而产生的冲击和保证视距，公路两相邻坡度段必须插入竖曲线。本文针对公路竖曲线，结合CASIO fx-5800P可编程计算器的特点，通过设计实用的公路竖曲线计算程序，提高计算工作的效率和精度。

关键词：竖曲线;变坡;曲线要素;程序;高程

中图分类号：TP393      文献标识码：A

文章编号：1009-3044（2019）27-0255-03

在公路施工测量工作中，尤其是路基工程的施工，现场需要频繁地计算施工位置的填挖高度，这就需要施工测量员在现场实时快速的计算出公路中桩的设计高程。根据公路的“纵坡、竖曲线表”计算中桩设计高程的过程较为复杂，采用CASIO fx-5800P可编程计算器运用程序进行计算是解决问题的有效手段。

1 公路竖曲线计算的模型

公路竖曲线计算的关键是模型。现行《公路路线设计规范（JTG D20-2017）》第8.6.1条规定，竖曲线可采用圆曲线或抛物线，对应的条文说明指出：“由于竖曲线的前后坡差很小，抛物线呈非常平缓的线形，因曲率变化较小，所以实际上与圆曲线几乎相同。在实际设计中，一般根据计算方便而采用圆曲线。”因此，本文采用极具代表性的圆曲线形竖曲线作为公路竖曲线计算的数学模型。

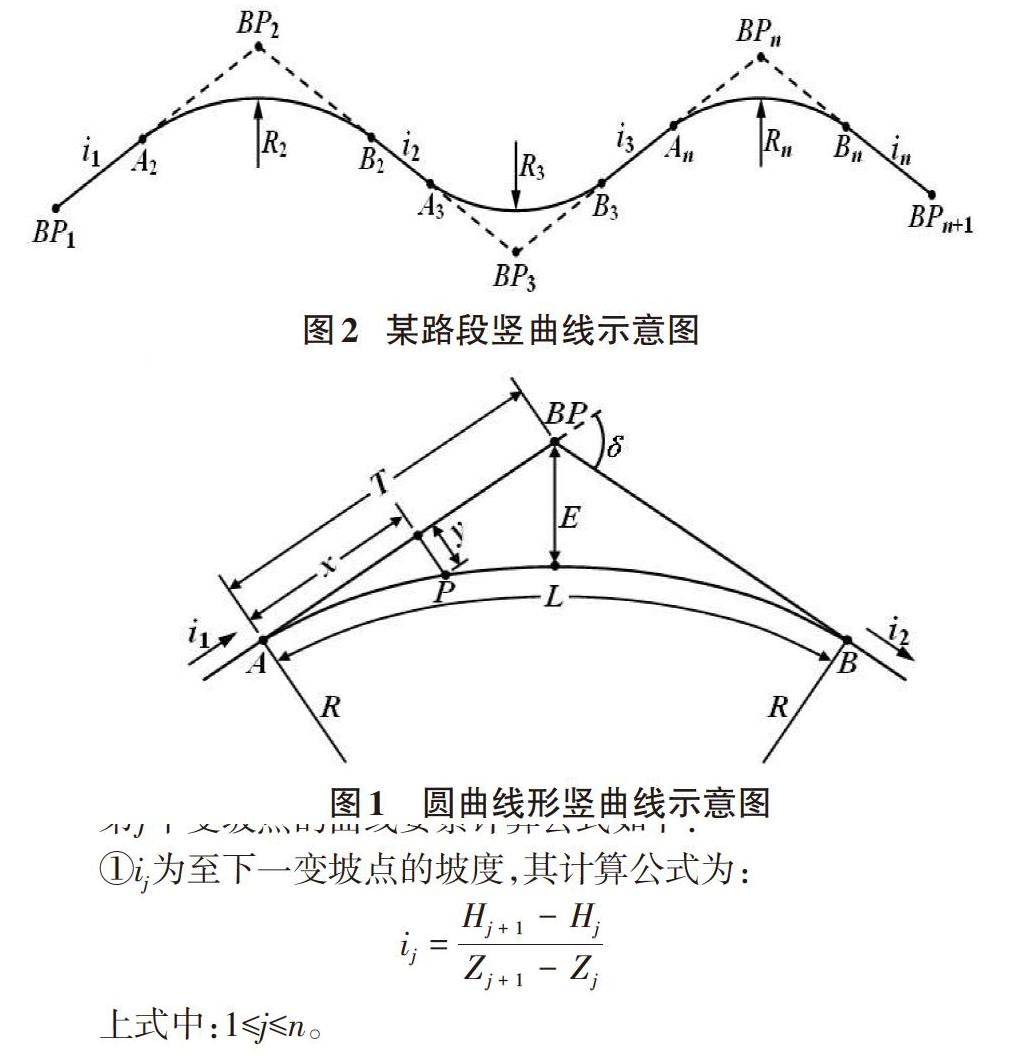
如图1所示，竖曲线半径为R，BP是变坡点，其桩号为ZBP、高程为H0。A是竖曲线起点，B是竖曲线终点，沿路线前进方向，i1为后坡坡度，i2为前坡坡度。当i1-i2>0时为凸曲线，当i1-i2<0时为凹曲线。曲线要素包括变坡角δ、切线长T、竖曲线长L和竖曲线外矢距E。

ZA为竖曲线起点A的桩号，ZB为竖曲线终点B的桩号，y为竖曲线上任一点P的切曲差。

2 公路中桩设计高程的计算

如图2所示，某路段的竖曲线有n+1个变坡点，编号依次为BP1、BP2、……、BPn、BPn+1（其中BP1和BPn+1应位于直坡段），竖曲线由n个纵坡组成，其坡度分别为i1、i2、……、in。其中：变坡点BP1（路段起点）的桩号为Z1，设计高程为H1;变坡点BP2的桩号为Z2、设计高程为H2、曲线半径为R2;……;变坡点BPn的桩号为Zn、设计高程为Hn、曲线半径Rn;变坡点BPn+1（路段终点）的桩号为Zn+1，设计高程为Hn+1。

2.1 曲线要素的计算

根据编程计算的需要，竖曲线的曲线要素应包括：①变坡点的桩号、设计高程、曲线半径、凸凹标记（凸为“+1”，凹为“-1”）、至下一变坡点的坡度;②切线长、曲线长和外矢距;③曲线起点的桩号、曲线终点的桩号。

路段起点BP1和终点BPn+1在直坡段，其曲线半径、凸凹标记、切线长、曲线长和外矢距均为0，曲线起点和终点的桩号均为BP1和BPn+1的桩号。

第j个变坡点的曲线要素计算公式如下：

①ij为至下一变坡点的坡度，其计算公式为：

②δj为变坡角，其计算公式为：

上式中：ij-1是变坡点j的后坡坡度，ij是变坡点j的前坡坡度。

③Fj为凸凹标记，其计算公式为：

④Tj为切线长，其计算公式为：

⑤Lj为竖曲线长，其计算公式为：

⑥Ej为竖曲线外矢距，其计算公式为：

⑦ZAj为曲线起点Aj的桩号，其计算公式为：

⑧ZBj为曲线终点Bj的桩号，其计算公式为：

用不同的j（1≤j≤n+1）值代入上述公式，可以求出全部变坡点的曲线要素。

2.2 中桩P设计高程的计算

计算公路中桩P的设计高程，首先应确定中桩P所在的纵坡，然后根据中桩P所在的纵坡区间运用不同的公式计算出切曲差，从而计算出中桩P的设计高程。

根据中桩P的桩号ZP与纵坡两端变坡点桩号之间的大小关系，可以确定中桩P所在的纵坡。若Zj

纵坡j一般可分为3个区间：①变坡点BPj～变坡点BPj处曲线的终点Bj;②变坡点BPj处曲线的终点Bj～变坡点BPj+1处曲线的起点Aj+1;③变坡点BPj+1处曲线的起点Aj+1～变坡点BPj+1。中桩P处于纵坡的不同区间上，其切曲差y的计算也不相同。设中桩P位于第j个纵坡上，切曲差yP的计算方法如下：

3 数据存储设计

数据存储设计是程序设计的核心。由n个纵坡组成的竖曲线，其计算时必不可少的曲线要素是由n+1个变坡点的桩号、设计高程、曲线半径等构成的，且每个变坡点的数据都具有相同的结构，因此宜采用矩阵来存储，每行对应一个变坡点，具体分配方案见图3。

按上述方案创建的矩阵称为曲线要素矩阵。若程序指定Mat A为曲线要素矩阵，在程序第1次运行结束后，可将Mat A赋值给其他矩阵，在下一次计算该路段前只需将其对应的曲线要素矩阵赋值给Mat A即可直接计算，无须重新输入曲线要素，有效地提高计算的效率。CASIO fx-5800P计算器有多个矩阵，因此一个计算器中可以同时存放多个路段的数据，能满足路线计算的需求。

4 曲线要素矩阵的创建

4.1 数据的输入方式

曲线要素的输入可采用三种方式：①直接在曲线要素矩阵中输入;②采用数据库子程序创建曲线要素矩阵;③采用曲线要素输入子程序。第三种方式是编写一个曲线要素输入子程序，通过调用子程序，用户采用人机交互的方式输入对应的数据，程序自动完成曲线要素矩阵的创建。为了提高程序的易用性，程序设计时应采用第三种方式。

4.2 输入项的选取

程序设计时，要确定好曲线要素输入的最小子集，凡能通过计算得到的要素，应采用程序自动计算的方式获得，以减少数据输入的工作量，降低出错的概率，从而提高效率。基于这一原则，公路竖曲线要素输入的最小子集可确定为变坡点的桩号、设计高程和曲线半径，用这3个参数通过计算可得到其他曲线要素。

4.3 曲线要素矩阵创建程序的设计

程序应具有新建（NEW）和数据更新（UPDATE）两个功能。若个别数据输入错误（或设计变更），可用矩阵编辑器修改Mat A中的对应数据后选择“数据更新”功能，让程序根据正确的数据重新计算其他曲线要素，并自动更新Mat A。曲线要素矩阵创建程序的主要代码如下：

5 公路中桩设计高程计算程序的设计算公路中桩的设计高程时，应先根据桩号确定其是否在Mat A所对应的路段区间上。若不在，应给出相应的提示信息;若在，则先确定中桩所在的纵坡，然后调用相应的曲线要素计算中桩的设计高程。公路中桩设计高程计算程序的主要代码如下：

本文的程序充分利用了程序的计算能力进行相关要素的计算，用户的数据输入量达到了最小化，增强了用户的使用体验。用户使用程序可快速、精确的计算出公路任意中桩的设计高程，同时程序还可自动判断桩号的合法性，健壮性好，用户使用非常方便。

参考文献：

[1] 何名灯.CASIO fx-5800P型计算器在线路测量中的应用[J].城市勘测，2018（1）：141-144.

[2] 向继平.CASIO fx-5800P公路坐标计算程序的设计与实践[J].电脑知识与技术，2018（33）：241-243.

[3] 覃辉，段长虹.CASIO fx-5800P矩阵编程计算器原理与实用程序[M].上海：同济大学出版社，2007.

[4] 王中伟.CASIO fx-5800P计算器与道路坐标放样计算[M].广州：华南理工大学出版社，2008.

[5] 顾孝烈，程效军.CASIO fx-5800P計算器土木工程测量计算程序开发与应用[M].上海：同济大学出版社，2007.

【通联编辑：光文玲】