基于相关技术的信号降噪算法

马琳琳

摘要：该文提出一种基于相关技术的周期信号降噪算法。该算法利用周期信号自相关函数的性质和DFT（discrete Fourier transform）从含噪信号中筛选出原周期信号的频率成分，再通过IDFT（inverse discrete Fourier transform）得到原周期信号。实验表明该方法不仅适用于提取被白噪声污染的周期信号，而且也可以用于提取被有色噪声污染的周期信号，并且该方法明显优于小波门限降噪方法。

关键词：相关;降噪;DFT

中图分类号：TN911      文献标识码：A

文章编号：1009-3044（2019）27-0245-03

Abstract： A new periodic signal de-noising method is proposed that uses correlation techniques. This new method can be interpreted as selecting the frequency components which mainly attributable to the original periodic signal from the noisy signal by using the correlation techniques and DFT （discrete Fourier transform）. Experimental results indicate that our proposed method is not only effective when the noise is white noise， but also can extract a periodic signal from the colored noise. It is also shown in the experiment that our method is better than wavelet thresholding de-noising methods.

Key words： de-noising; correlation; DFT

1 背景

周期信號是很常见的一类信号，由于它在含噪信道中传输时，易被噪声污染，因此需要对含噪的周期信号进行降噪。最早的降噪算法是利用DFT对信号进行低通滤波，虽然这样完全消除了高频噪声，但是，与此同时也失去了信号一些重要的细节信息。随着小波的出现，人们开始用小波方法对含噪信号降噪。在过去二十年里，国内外的相关研究成果很多，Witkin在1983年提出尺度空间滤波算法[1]，Xu在此基础上，于1994年提出了空域相关滤波（SSNF）方法[2]。由于这种降噪算法的效果与相关系数的定义关系密切，因此只有在特定情况下，这种算法的降噪效果才显著。基于低通滤波的思想，Donoho在1994年从另一个角度提出了小波门限降噪算法[3]，并于95年完善成软门限降噪算法[4]，该方法提取被高斯白噪声污染的信号非常有效。近些年来，人们在软门限降噪算法的基础上，提出了许多改进的软门限降噪方法[5]。虽然这些方法都可以对含噪的周期信号进行降噪，但是这些方法非常繁琐，如需要在[L2（R）]空间中找到合适的小波基来分解含噪信号;决定分解层数;计算门限值等。此外，这些算法对有色噪声污染的周期信号提取的效果很差。而本文算法相对简便易行，而且对周期信号的降噪效果明显优于小波门限算法。尤其当噪声是有色噪声时，本文算法的优势更加显著。

基于周期信号自身的特点，一些研究者也提出了针对周期信号的降噪算法，这些算法大多只适用于周期信号被白噪声污染的情况，文献[6]运用周期信号自相关函数的性质成功地检测出被噪声严重污染的周期信号，但是并没有给出对该周期信号进行提取的方法。文献[7]在文献[6]的基础上给出了从白噪声中提取周期信号的方法，然而由于该方法属于时域降噪方法，因此它需要先估计出原周期信号的周期。本文算法在文献[6]的基础上结合DFT可以准确提取出周期信号，而且不需要估计信号的周期，即使噪声是有色噪声，本文算法也可以成功地提取出周期信号。

2 算法原理

2.1 周期信号自相关函数的性质

3 算法

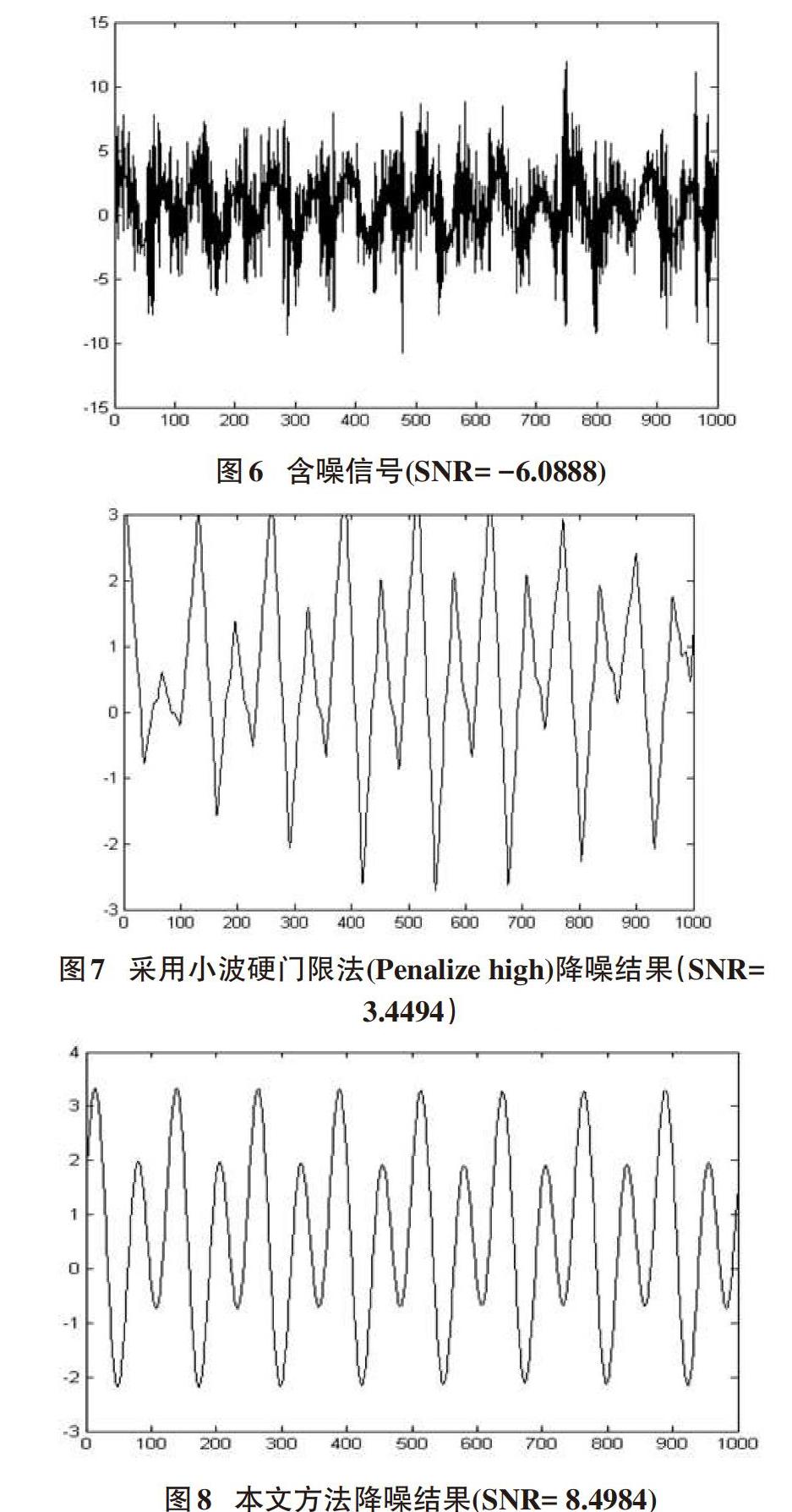
设是[V（t）]的有限序列观察值，[v（t）=s（t）+n（t），t=0，1…N-1]，其中[s（t）]是周期为（[T

1）对[v（t）]进行[N]点DFT，并得到频域变换系数序列[{Vk}，k=0，1…N-1]。

2）计算[v（t）]的周期自相关函数[{Rv（τ），τ=0，1…N-1}]，去掉（通常由噪声的类型和噪声的功率所决定）后得到序列[{Rv（t+m+1）}]。为了保留足够多的原信号的信息取值不能过大。

3）对[{Rv（t+m+1）}]进行[N]点DFT（通过补0把[{Rv（t+m+1）}]的长度扩充到[N]），并得到频域系数[{RVk}，][k=0，1…N-1.]

4）采用以下方法修改[Vk]的值：

4 仿真结果

以下两组实验中的小波门限法均采用db3小波基，并且对含噪信号都进行五层分解。

实验一：把均匀分布在[-0.5 0.5]的白噪声叠加到周期信号

[s（t）=cos（16πt/N）+2sin（32πt/N），][N=1000]（见图1）上，得到信噪比为-0.5520dB的被严重污染的信号（图2）。在该实验中，分别采用文献[7]的方法、小波门限方法和本文方法对该含噪信号进行降噪。由于实际计算的白噪声的自相关函数不能在[τ>0]时立刻衰减到0，因此[m]取0时效果不理想。本实验[m]取6时效果较好。图3至图5分别给出了这些方法的降噪结果，其中图4采用Heuristic SURE方法选择门限（针对本实验信号，这种方法降噪效果比其他小波门限降噪方法好）。图3说明，由于信号被严重污染，采用文献[7]的方法不易准确估计出原信号的周期，该方法并没有完全去除高频的噪声。从图4可以看出，小波门限降噪后波形的平滑性较差。图5表明，本文的方法降噪后的波形与原信号几乎无差别，不仅保留了周期性，还完全消除了高频的噪声，并且信噪比相对于小波门限法增加了约12dB。由实验一可以得出结论：虽然小波门限降噪法对时变信号降噪效果很好，但是对平稳的周期信号降噪，与DFT结合的算法要比小波门限法更具有优势。

实验二：把AR（3）噪声叠加到同样的周期信号上，得到信噪比为-6.0888dB的含噪信号（见图6），分别采用小波门限法和本文方法进行降噪。从图6可以看出，噪声的功率很大，因此这里[m]需要取较大的值（[m=159]）以消除噪声的影响。事实上，当噪声功率过大时，噪声自相关的值也会很大，因此衰减到0的速度较慢，需要延迟许多阶后才能近似到0，但是[m]取值不易过大，否则会损失大量原信号的信息。图7给出了用Penalize high threshold方法选择门限对信号降噪后的波形（在本实验中，这种方法降噪效果比其他小波门限降噪方法好）。从图7可以看出小波降噪后的波形的中间段与原始信号较像，两端失真较大。图8是采用本文算法降噪后的结果，可以看出降噪后波形与原信号几乎没有区别。并且信噪比相对于小波方法降噪结果提高了5dB。充分说明了本文算法的优势。

5 结束语

本文在文献[6]的基础上，提出了一种基于相关技术的周期信号频域降噪算法，该算法简单易行，可以用于提取被噪声污染的周期信号。实验表明通过适当调节[m]的取值，可以提取被白噪声或有色噪声污染的周期信号，并且提取的信号波形几乎与原信号完全一样。本文算法的降噪结果优于文献[7]算法的降噪结果，并且比小波降噪算法更具有优势。大量的对比实验还表明当白噪声的功率较小时，本文算法降噪后的信噪比可以比小波门限法降噪后的信噪比提高约20dB，当有色噪声的功率较小时，本文算法的优势则更加显著。

参考文献：

[1] Witkin A. Scale space filtering[M]. Proc 8th International Joint Confence Artifical Intelligence， 1983： 1019-1021.

[2] Mallat S， Hwang W L. Singularity detection and processing with wavelets[J]. IEEE Trans. Inform. Theory， 1992， 38（2）： 617-643.

[3] Donoho D L， Johnstone I M. Ideal Spatial Adaptation by Wavelet Shrinkage[J]. Biometrika， 1994（81）： 425-455.

[4] Donoho D L， Johnstone I M. Adapting to unknown smoothness via wavelet shrinkage[J]. Journal of the American Statistical Association， 1995（90）： 1200-1224.

[5] Lang M， Guo H. Noise Reduction Using an Undecimated Discrete Wavelet Transform[J]. IEEE Signal processing letters， 1996， 3（1）： 10-12.

[6] LEE Y W， CHEATHAM J R， WIESHNER J B. Application of Correlation Analysis to the Detection of Periodic Signals in Noise[J]. Proceedings of the I.R.E， 1950， 38（10）： 1165-1171.

[7] Schilling R J， Harris S L. Fundamentals of Dig ital Signal Processing—— Using MATLAB[M]. Xi AN： XiAN JIAOTONG UNIVERSITY PRESS， 2005.

【通聯编辑：谢媛媛】