灰狼算法优化BP神经网络的图像去模糊复原

王海峰，李 萍，王 博，翟帅华，蔡 楠

(宁夏大学 物理与电子电气工程学院，宁夏 银川 750021)

1 引 言

由于运动、抖动、电子干扰等影响因素的存在，导致图像在拍摄、传输和储存时会产生一定的退化。图像复原可以最大程度地除去模糊以及干扰，使复原后的图形与原始图像更相似。作为图像模糊最典型且常见的模型之一的高斯模糊，其点扩散函数普遍应用到图像处理系统中，因此可以利用其特性来近似模拟一些图像的退化过程。

传统的图像复原方式有很多，如维纳滤波法[1]、正则化方法[2]、迭代盲反卷积[3]、约束最小二乘法[4]等。近年来随着神经网络学习热度的不断增加，在图像复原领域已经有很多神经网络模型在实际应用中发挥作用，Zhou[5]提出将神经网络应用到图像复原。李伟等人用优化算法对神经网络的结构进行优化，然后利用优化后神经网络学习和泛化能力，使复原的图像在主观视觉和定量分析上取得不错的效果[6]。文献[7]分别利用遗传算法与蚁群算法对BP神经网络进行优化并运用到图像复原领域，实验验证表明改进算法比传统BP网络复原图像有较大优势，复原后的图像更加清晰。文献[8]采用粒子群算法进行散焦模糊图像的复原，经过复原实验获得的结果清晰度比传统L-R复原效果更好，振铃较少。文献[9]提出了基于粒子群算法的BP神经网络图像复原，该作者将BP神经网络的初始权值和阈值作为粒子群的优化目标进行全局寻优，该算法在图像复原中收敛精度取得了不错的效果。文献[10]提出了一种基于布谷鸟算法的BP 神经网络( Cuckoo Search-Back Propagation，CS-BP) 图像复原方法。该实验方法取得了较好的复原效果。提高了复原模型收敛精度，增强了训练结果的稳定性，但是复原模型训练的时间却增加了。

本文将BP神经网络作为工具用于图像复原，针对传统BP神经网络算法的初始阈值和权值是随机的，容易陷入极小值，运算结果存在随机性的缺点，提出利用灰狼优化算法的较强的全局搜索能力来尽可能消除BP神经网络对初始参数的过度依赖。利用训练好的模型对测试集进行测试，以达到图像复原的要求。

2 传统复原算法介绍

2.1 维纳滤波复原

维纳滤波复原是一种有约束条件的以最小均方误差为准则的退化图像复原方法，其原理是将图像通过滤波器处理，使经过滤波复原获得的图像与原始图像的均方误差最小。如公式(1)所示。

(1)

其中：E[*]为数学期望算子。如果假设复原图像的灰度值与图像中灰度级是线性相关的，图像与噪声互不相关，并且其中之一是零均值。在假设成立时，其频域表示式为：

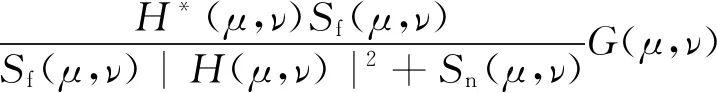
(2)

公式(2)中H*(μ,ν)为退化函数H(μ,ν)的复共轭，Sn(μ,ν) 以及Sf(μ,ν)表示噪声以及原始图像的功率谱。

在退化图像的复原中，对于高信噪比的区域，在复原过程中可以有效抑制噪声放大，但是在实际操作中由于无法准确地知道噪声以及原始图像的功率谱的值，而导致复原效果不好。

2.2 L-R迭代非线性复原

L-R迭代非线性复原方法由Lucy和Richardson根据贝叶斯定理最先提出的基于迭代的非线性算法。该算法可以在对噪声信息未知的情况下利用已知的点扩散函数进行退化图像的复原。可以有效地处理噪声问题，并且复原效果不错。如果噪声过大，在复原过程中噪声会随着迭代次数的增加而逐渐放大，增加振铃效应。

2.3 基于BP神经网络的复原

BP神经网络是一种信号前向传递、误差反向传播的多层神经网络，是应用最广泛的网络之一[11]。在网络传播的过程中，包括两个主要的过程：前向传播和误差反向传播。BP神经网络能够模拟任意输入和输出之间的非线性映射关系。不仅能够学习处理已有的经验，还能够学习获得未知函数输入输出的关系，在处理复杂非线性问题、优化计算、逻辑推算方面有很大的优势。因此选择BP神经网络可以在点扩散函数未知的情况下实现退化图像与原始图像间非线性映射关系的拟合。但是算法对初始权值与阈值的过度依赖会导致算法在退化图像复原过程中陷入局部最小值，导致误差过大，训练失败。

3 灰狼优化算法

灰狼优化( Grey Wolf Optimizer，GWO) 算法[12]是Mirjalili 等人在2014年提出的一种新型群智能优化算法。GWO算法模仿灰狼的领导层次以及通过模拟灰狼寻找、包围和攻击猎物等狩猎机制的过程来完成最优化工作。4种类型的灰狼，如α、β、δ和ω被用来模拟领导阶层，分别定义为最优解、优解、次优解和待选解。此外，还实施了寻找猎物，包围猎物和攻击猎物3个主要捕食步骤。灰狼种群明确的等级制度对于狼群实施高效狩猎有着非常重要的作用。捕猎的过程是由头狼带领完成，该过程为所有灰狼聚集在一起进行搜索、追踪、追逐、逼近猎物，然后灰狼按照一定的指导方式多方向包围猎物，当包围圈足够小并且时机成熟时，狼群距离猎物最近的β狼和δ狼在头狼的命令下发起攻击。在追逐逃跑猎物过程中，其余的狼群个体会及时对追赶猎物的灰狼进行补充，最终实现整个狼群包围圈对猎物的跟踪变换，从而达到对猎物不断实施各个方位的进攻，成功完成对猎物的捕食。

文献[13]的实验研究表明，灰狼优化算法在全局寻优方面明显优于粒子群优化算法(Particle Swarm Optimization，PSO)、遗传(Genetic Algorithm，GA)算法等智能优化算法。因此，本文BP 神经网络的权重和阈值可以利用GWO 来优化。

3.1 社会等级

为了方便将灰狼的社会等级制度利用数学模型来描述,开发者在设计灰狼优化算法过程中,将α狼、β狼、δ狼以及ω狼分别定义为最优解、优解、次优解和待选解。狼群的捕猎过程由α狼、β狼、δ狼进行引导,ω狼处于跟随状态。假设狼群有灰狼N只,搜索空间为M,任意一只灰狼的位置记为xi=(xi1,xi2,…xim),种群中最优个体记为α,将要捕到的猎物对应全局最优解。该算法的搜索过程:首先随机产生一组解作为候选解,在迭代进化过程中,分别由适应度较好的α狼、β狼、δ狼对当前猎物的位置进行评估,剩下的狼评估自身位置并跟随。

3.2 包围猎物

灰狼个体之间的距离、子代灰狼个体位置的更新方式如下所示：

D=D=|C·XP(t)-X(t)|，

(3)

X(t+1)=XP(t)-A·D，

(4)

A=2a·r2-a，

(5)

C=2r1，

(6)

其中:D表示个体与食物的距离，t表示当前迭代的次数，C向量是对猎物的扰动，Xp代表目标的位置，X是当前个体的位置。在迭代过程中a从2线性递减至0，如公式(5)所示;r1、r2是[0，1]内的随机向量。

(7)

3.3 狩猎

在灰狼群体的捕食猎物过程中，如果位于领导层级的灰狼侦查到猎物的位置，α狼会会同其他等级的灰狼对整个灰狼种群进行指导运动。指挥狼群接近猎物，最终捕获猎物。个体更新方式描述如下：

Dα=|C1·Xα(t)-X(t)|，

(8)

Dβ=|C2·Xβ(t)-X(t)|，

(9)

Dδ=|C3·Xδ(t)-X(t)|，

(10)

其中：C1、C2、C3代表对α、β、δ的随机扰动，Xα、Xβ、Xδ分别表示α、β、δ的当前位置。以下公式指导ω狼的前进方向以及距离：

X1=Xα-A1·Dα，

(11)

X2=Xβ-A2·Dβ，

(12)

X3=Xδ-A3·Dδ，

(13)

X(t+1)=(X1+X2+X3)/3.

(14)

子代灰狼的最终位置由公式(14)决定。灰狼算法原理图如图1所示。

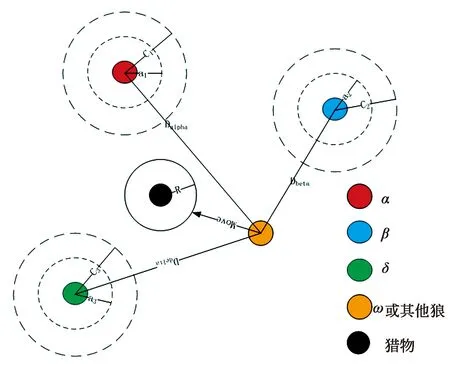
图1 灰狼算法原理图Fig.1 Schematic diagram of the gray wolf algorithm

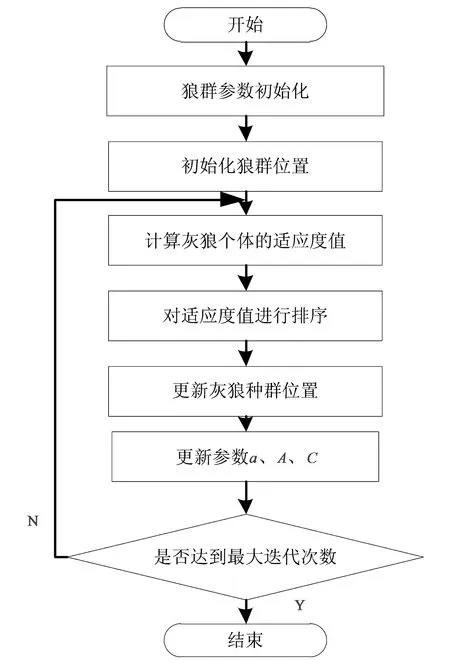
图2 灰狼算法流程图Fig.2 Gray wolf algorithm flow chart

从图中可以看出，灰狼算法的寻优过程是通过α、β、δ狼对猎物的位置进行评估，狼群内的其他个体根据这个评估标准在猎物的周围进行随机位置更新。

灰狼优化算法的标准流程如下：

第一步，灰狼算法参数初始化。设置灰狼群的大小N、迭代次数M、搜索空间维度、搜索空间的上下界。

第二步，初始化灰狼的位置Xi。

第三步，计算灰狼个体的适应度值。

第四步，根据适应度值得大小进行排序，找出排在前三位的个体，定为最优解、优解、次优解。

第五步，根据公式更新灰狼种群的位置。

第六步，更新计算a、A、和C的值。

第七步，判断最优解是否满足条件，若满足终止条件输出最优解，否则转向第三步。

灰狼算法的流程图如图2所示。

4 GWO-BP神经网络模型

4.1 BP神经网络复原结构的设计

Robert Hecht-Nielson的研究表明，对于任何在闭区间内的连续函数可以用单隐含层的BP网络来近似模拟，因此一个含有单隐层BP网络可以完成任意的n维到m维的映射[14]。本文将利用单隐层的BP神经网络进行图像复原。

数字图像中在高斯模糊过程中目标像素点与它邻近的像素点存在密切关系，像素点的影响随着距离的增大而逐渐减小，这种现象总结如下：一幅图像中任意位置的像素点与其相应的模糊图像对应位置的邻域存在很大的相关性。为了得到比较接近原始图像的复原效果，需要考虑任意像素点的邻域对其的影响。将任意位置及其相邻点的像素值作为复原模型的输入，使用3×3的滑动窗口从左向右依次扫描整张图像，将扫描得到的数据作为神经网络的输入，相对应的原始图像中对应位置的灰度值作为网络模型的输出。用于图像复原的BP神经网络的拓扑结构经过多次调试确定为9∶20∶1 ,隐含层激励函数采用Sigmoid函数，输出层采用线性函数。BP神经网络复原拓扑结构如图3所示。

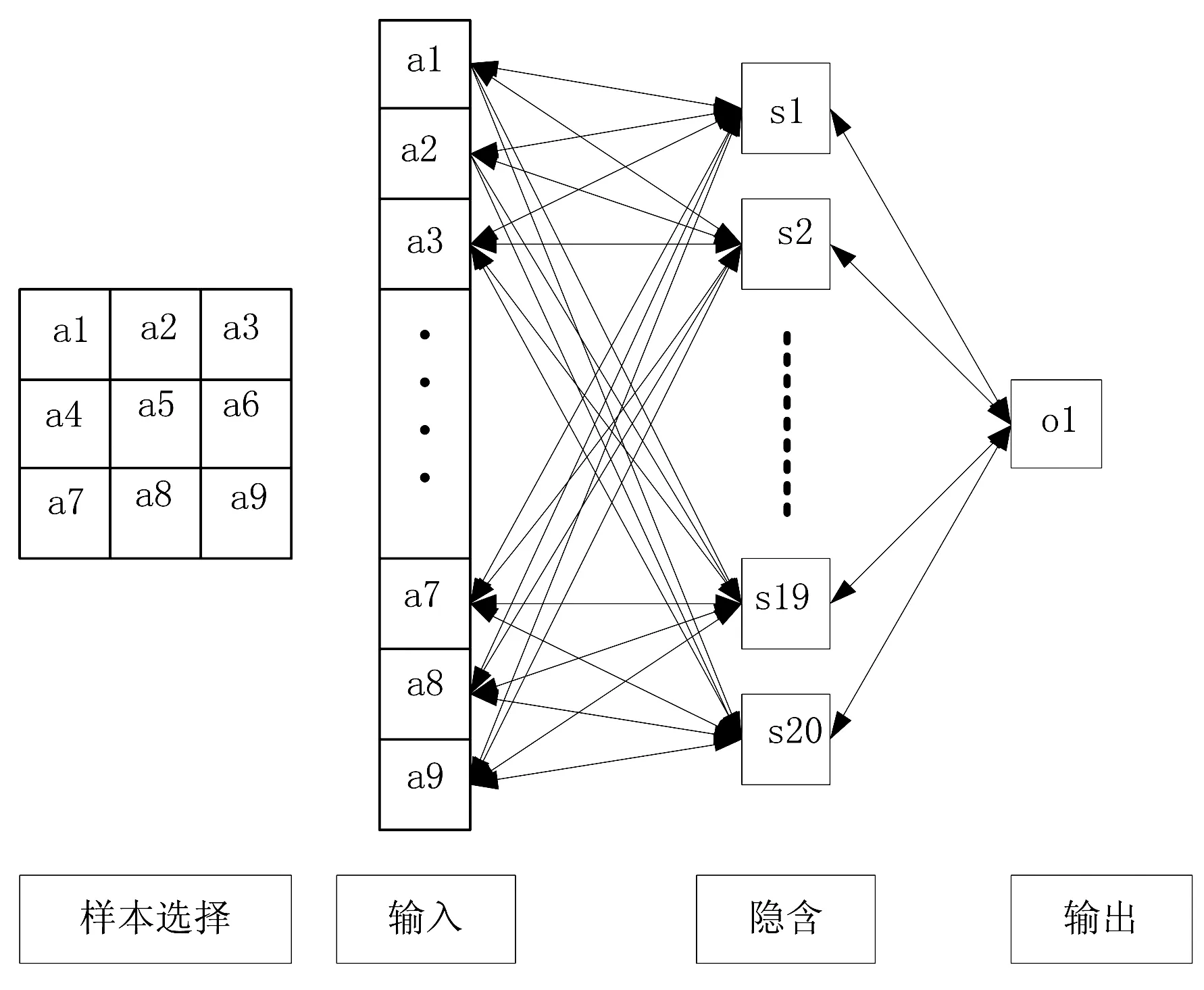
图3 BP神经网络复原拓扑图Fig.3 BP neural network restoration topology

4.2 GWO-BP神经网络算法设计

灰狼算法是具有良好全局搜索能力的群智能算法，能够加快网络模型的收敛速度，提高模型的精度，利用灰狼算法的优点与BP神经网络优秀的局部调节能力，设计基于灰狼算法优化的BP神经网络算法(GWO-BP算法)，该算法的基本思路是：将BP神经网络的权值与阈值作为灰狼个体的位置信息，利用灰狼算法良好的全局寻优能力大致搜索出最优权值、阈值的范围，将搜索得到的最优权值和阈值作为BP神经网络的初始值，以此改变由于BP神经网络初始值选取不当导致的网络收敛速度慢与容易陷入局部极小的缺点。

4.2.1 灰狼优化算法的改进

由于灰狼算法的收敛方式不是直线下降的，传统的线性收敛不能完全展现灰狼算法的收敛过程，在考虑到算法的收敛过程这一问题上提出了基于余弦的收敛因子公式，如公式(15)所示：

(15)

经过改进后的收敛因子以非线性的方式从2递减为0，在算法运算开始阶段，与原来的线性收敛相比改进后的收敛因子衰减速度减小，这种方式能够更好地寻得全局最优解。在算法后期，收敛因子衰减速度加快，对于局部最优解的寻找更加准确。

对标准灰狼算法数学模型的介绍，可以看出α、β、δ狼对于ω狼的影响程度是一样的，但是灰狼算法具有严格的等级制度，影响程度从理论上应该与灰狼的等级相匹配。在设计的灰狼算法中，经过对适应度排序得到的α、β、δ3个当前最优解，由于这3个领导层相同的指导力度使得灰狼算法的收敛速度有所减小，容易陷入局部最优。在标准算法中加入一种基于动态位置向量指导的比例权重，利用不断地动态调整指导权重，增加算法的环境适应能力，调节算法的搜索能力加速算法收敛。

权重比例调节计算公式如下:

(16)

ω1对应于ω狼对α狼的学习率。

(17)

ω2对应于ω狼对β狼的学习率。

(18)

ω3对应于ω狼对δ狼的学习率。

改进后的灰狼算法的子代灰狼的最终位置由公式(19)决定。

(19)

4.3 GWO-BP复原算法步骤

第一步：选择进行神经网络训练的样本h并对其进行高斯模糊处理，对处理过的图像f进行归一化处理，

第二步:建立一个含有一层隐含层的BP神经网络复原模型，图像h作为输出，训练样本f作为神经网络的输入。

第三步：初始化灰狼群，神经每一层的权值和阈值作为改进灰狼算法的优化对象，进行灰狼算法全局寻优，当系统达到最大迭代次数或误差达到设定值时算法停止迭代，输出神经网络的最佳初始值。

第四步：利用优化获得的权值和阈值进行BP神经网络训练，若训练性能达到要求则进行下一步，否则返回第三步重新训练。

第五步：进行目标图像的复原，对神经网络的输出进行反归一化处理，显示复原图像。

5 实验结果分析

该实验在matlab2016b中进行，此次实验分为两部分，一是退化图像复原模型的训练，二是利用模糊图像测试。对于图像的边界问题，考虑到图像最外层的像素没有对应的输出，为了解决这个问题，在已知图像中某点灰度值的变化同它临近点的灰度值有很大的联系，像素点距离越小，对中心像素的影响就越大条件的基础上，对实验与测试图像进行边界复制，使退化图像的所有像素点都有对应的输出。

5.1 改进GWO-BP网络的学习与训练

采用图像大小为256×256的Lena图像作为训练图像，如图4所示。(a)为原始图像，(b)为经过高斯模糊处理后的图像。

图4 训练图像Fig.4 Training images

5.2 图像复原实验

利用Cameraman与barbara经过高斯模糊的图像作为本文算法的验证图像，用BP、PSO-BP以及维纳滤波的方式以及文章中提出的改进GWO-BP算法进行图像复原验证。不同的模型复原效果如图(5)、图(6)所示。

由图(5)、图(6)可以看出，BP神经网络图像去模糊复原效果好于维纳滤波复原法、L-R复原；PSO-BP复原较BP复原在清晰度上得到改善，而本文提出的改进GWO-BP(IGWO-BP)复原方法通过视觉可以看出与原始图像近似，图像的轮廓以及部分细节的视觉效果提高了很多。

图5 Cameraman模糊图像复原对比Fig.5 Cameraman blurred image restoration comparison

图6 Barbara模糊图像复原对比Fig.6 Barbara blurred image restoration comparison

为了更加直观地对比图像复原的效果，文章采用峰值信噪比(PSNR)、结构相似度(SSIM)以及归一化均方误差(NMSE)来对图像复原效果进行比较与评价，评价结果由表1、表2给出。

通过表1、表2的数据可以直观地看出本文提出的算法具有更大的峰值信噪比、更好的结构相似速度以及更小的归一化均方误差。这是由于峰值信噪比越大，图像的复原效果越好；归一化均方误差越小，复原效果越好。

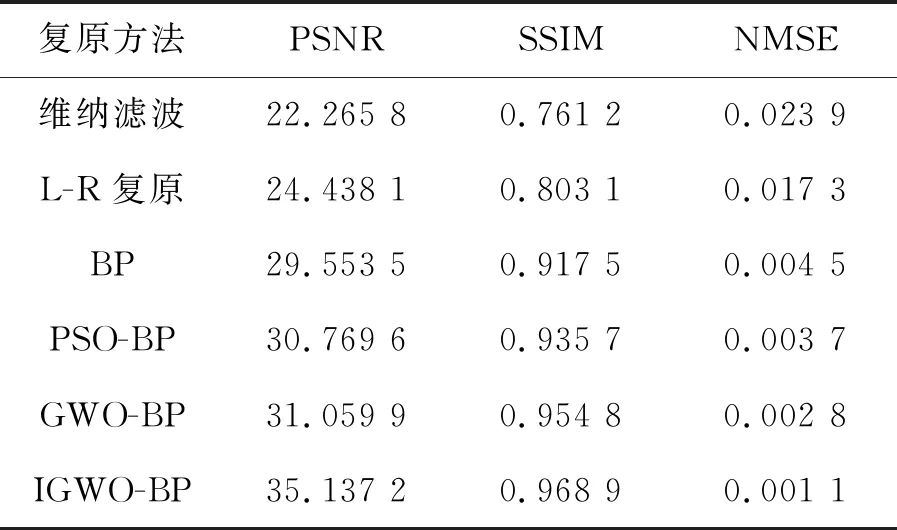
表1 Cameraman复原结果数据Tab.1 Cameraman restoration results

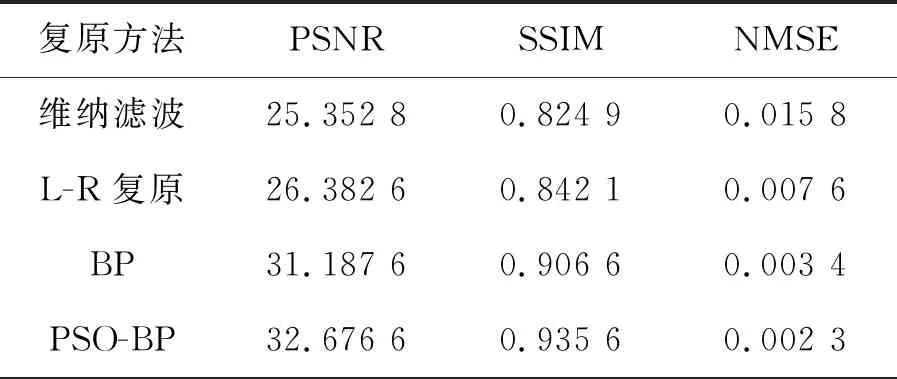
表2 barbara复原结果数据Tab.2 Barbara restoration result

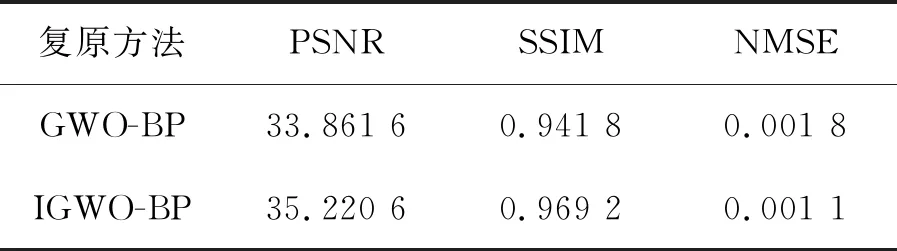
续 表

6 结 论

对于高斯模糊图像的复原，本文提出了基于改进灰狼算法优化神经网络的图像去模糊。利用灰狼算法对神经网络的权值与阈值进行优化，并在此基础上通过改进灰狼算法收敛因子与动态比例权重的灰狼位置更新机制，加强了算法全局寻优能力，增加算法的环境适应能力。研究结果表明，本文所提方法在主观视觉与客观评价上与维纳滤波、L-R复原、BP复原、以及PSO-BP图像复原算法相比其结果令人满意。在引入并改进灰狼算法后，灰狼优化BP神经网络对模糊图像的复原效果表明本文所提出的改进算法图像复原后的相似度分别达到96.89%以及96.92%，误差减小到0.11%，满足了实际应用的要求。