改进的Kullback-Leibler复非负矩阵分解语音增强算法

许铭，王冬霞，周城旭，张伟

改进的Kullback-Leibler复非负矩阵分解语音增强算法

许铭，王冬霞，周城旭，张伟

(辽宁工业大学电子与信息工程学院，辽宁锦州 121001)

针对单通道非负矩阵分解语音增强算法忽略相位信息的问题，提出了一种改进的Kullback-Leibler复非负矩阵分解的语音增强算法。该算法考虑到传统非负矩阵分解算法在复频域中增强语音时目标函数的影响，构建了一种适用于复频域的Kullback-Leibler散度下的目标函数，同时采用频谱一致性约束相位谱补偿算法，使其重构出的语音数据相位谱得到进一步的调制。实验结果表明，对于不同的非平稳噪声，所提出的算法在不同信噪比下均取得了较好的语音增强效果，尤其在低信噪比条件下(0 dB以下)语音增强效果较为明显，性能评估指标的增量较高，较好地克服了由传统相位谱补偿算法造成的信源失真率较低的缺点，进一步减少失真，抑制背景噪声，实现语音增强。

复非负矩阵分解；相位谱补偿；语音增强

0 引言

语音增强旨在去除带噪语音信号中的噪声成分，以获得较为纯净的语音信号，从而提高语音信号的质量和语音可懂度。经典的单通道语音增强算法包括谱减法[1]、统计模型法[2]、子空间分解[3]等算法。这些算法在平稳噪声条件下具有良好的噪声抑制效果，但在非平稳噪声环境下却不尽人意，语音增强的性能有限。

非负矩阵分解(Non-negative Matrix Factorization, NMF)是一种良好的机器学习和数据挖掘的方法[4]。研究表明，该算法可以将带噪语音信号的幅度(或功率)谱近似分解为时变系数频谱与静态基频谱的乘积，然后在训练纯净语音和噪声信号的子空间谱的基础上，更新带噪语音的系数矩阵，最后重构原始纯净语音[5]。

但是该算法往往假设幅度(或功率)谱具有可加性，没有考虑到重构时原始语音相位信息的影响。为了解决这一缺点，有学者提出复非负矩阵分解(Complex Non-negative Matrix Factorization, CNMF)算法[6-7]，该算法在复频域对观测信号进行处理，利用信号每个频点的相位谱信息来获得幅度谱的最优估计。由于复频域的限制，该算法在度量原始信号复频谱与重构的复频谱间误差的目标函数时具有局限性，仅限于采用欧几里得距离(Euclidean Distance, EUC)模型，且该模型在度量原始数据与重构数据间的误差时，采用平方运算而导致异常点误差被放大，影响重构数据的精度[8-9]。因此，本文利用(Kullback-Leibler, KL)散度模型构建目标函数来度量误差，以提高CNMF算法的性能。

考虑到重构原始纯净语音时采用带噪语音相位谱会造成语音信号失真，限制增强性能[10]，故文献[11]提出了相位谱补偿算法(Phase Spectrum Compensation,PSC)调制带噪语音的相位谱，以提高增强后语音信号的质量和可懂度，但该方法在不同的背景噪声环境下参数很难确定，且反对称函数的应用造成部分相位谱的偏差被放大，降低了信源失真率(Source Distortion Rate, SDR)。

因此，为了有效的利用相位信息，本文提出改进的KL-CNMF算法相位谱补偿语音增强模型，在提高CNMF算法噪声抑制能力的同时，根据带噪语音、噪声信号与纯净语音的矢量关系，引入傅里叶变换一致性约束[12-13]改进文献[11]的算法，进一步减少在不同环境噪声下由相位信息的影响而造成的语音失真现象，较好地保留了语音信号的基本信息，减少了残留噪声，提高了语音质量和可懂度。

1 Kullback-Leibler复非负矩阵分解

故利用式(6)、(7)的不等关系可将式(5)右侧进一步改写为

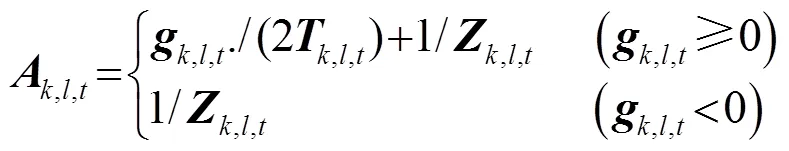
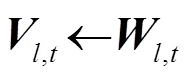
迭代算法总结如下：

2 改进的相位谱补偿算法

改进的PSC算法虽然造成了带噪语音信号与估计的噪声信号向量大小与角度的改变，但其针对每个频点相位谱的失真，利用频谱一致性约束进行调制，保证了调制算法的时变性，同时使相加后得到的相位谱进一步接近纯净语音相位谱且不会因反对称函数造成相位谱失真被放大的现象。

图1 PSC算法与改进的PSC算法相位估计向量图

补偿后的纯净语音频谱估计为

3 改进的KL-CNMF语音增强算法

语音增强算法结构如图2所示，即包括两个阶段：学习和增强。

图2 改进的KL-CNMF相位补偿语音增强算法框图

增强阶段包括3个部分：(1) 系数矩阵更新、(2)相位调制、(3) 增强信号重构。

(1) 系数矩阵更新阶段

(2) 相位调制阶段

利用式(22)分别估计出经过STFT的带噪语音信号和经过KL-CNMF算法估计出的噪声信号的频谱一致性约束，然后，利用式(23)、(24)进行相位谱补偿，最后，得到修正的相位谱如下：

(3) 增强信号重构阶段

采用维纳滤波求带噪语音信号增益的原理，输入重构出的语音和噪声幅度谱，求得带噪语音增益函数，即

结合式(28)求得的带噪语音增益与改进的KL-CNMF算法估计出增强的相位谱和幅度谱，得到纯净语音谱为

最后，利用逆STFT变换得到时域上的语音增强信号。

4 实验结果与分析

4.1 实验参数设置

4.2 语音质量与可懂度分析

实验中选择3种非平稳背景噪声：噪声能量主要分布在低频段的Factory1工厂车间噪声、Babble餐厅内嘈杂噪声，以及Hfchannel噪声，将本文提出改进的KL-CNMF语音增强算法与标准NMF算法、文献[7]算法、KL-CNMF语音增强算法、文献[11]算法的性能指标进行比较。采用客观质量评估方法(Perceptual Evaluation of Speech Quality, PESQ)、信源失真率(Source Distortion Rate, SDR)、语音的短时客观可懂度(Short Term Objective Intelligibility, STOI)和分段信噪比(Segmental Signal-to-Noise Ratio, SSNR)作为语音增强算法性能的客观评估标准。

如图3给出了标准NMF(KL)、文献[7]与KL-CNMF算法的目标函数关于迭代次数与度量误差的关系图。如图3所示，随迭代次数的增加，各算法逐渐收敛，且KL-CNMF算法收敛速度较快，这说明在复频域NMF算法的收敛速度要明显快于标准频域NMF算法。在迭代次数到达约35次前，在复频域NMF算法的误差值较小。当迭代次数超过35次以后，文献[7]算法的误差值不降反增，而KL-CNMF算法误差值一直保持收敛且最小，即采用KL散度计算目标函数的精度要高于欧式距离模型，可以较好地提高目标函数度量误差的精度，保证算法的性能。

图3 各算法目标函数关于迭代次数与误差的收敛图

表1为四种不同的NMF算法单次学习联合字典矩阵所消耗时间的情况(设置迭代次数为50)。可见，文献[7]算法与基于EUC模型的标准NMF算法训练耗时较长，而本文提出KL-CNMF算法与基于KL散度模型的标准NMF算法训练耗时约降低了50%。这说明本文提出的算法虽然增加了计算的复杂度，但是应用KL散度模型下的目标函数仍能够保持其应用在标准NMF算法中的特质，降低了字典的训练时间，提高了算法的实用性。

表1 不同算法的训练时间比较

表2为3种背景噪声和不同的信噪比条件下的PESQ与SDR平均值比较，而图4、图5和图6表示为3种背景噪声和不同信噪比下各平均值增量比较[14]，可以看出在同一种噪声条件下，随着信噪比(Signal Noise Rate, SNR)的增加，各算法SDR、STOI、SSNR评估值的增长量逐渐下降，PESQ评估值增量较为稳定。这说明虽然各算法增强性能逐渐减弱，但其仍能够在一定程度上提高语音质量和可懂度，本文提出算法在不同的噪声条件下均具有更高的性能指标，且其增长量较高，说明该算法无论在低频或高频背景噪声条件下均具有较好的稳定性与增强性能。对比各算法在相同信噪比及不同噪声条件下的评估值增量，发现同一算法的PESQ、STOI、SSNR评估值的增量总体趋势为Factory1>Hfchannel>Babble，SDR评估值增量的总体趋势为Hfchannel >Factory1> Babble，这说明在同一信噪比不同噪声的影响下，各语音增强算法均能够提高语音质量与可懂度，且在Factory1背景噪声条件下各算法的性能较好，而在Hfchannel背景噪声条件下，各算法增强后的语音失真较少，且可以看出本文提出算法具有较强的噪声抑制能力，在Hfchannel噪声条件下性能最优。

表2 不同噪声背景下不同语音增强算法PESQ与SDR平均值比较

在不同的背景噪声环境下，各语音增强算法的PESQ、STOI、SDR、SSNR平均值如图4～图6所示，对比标准NMF算法与其他算法的评估值增量，可以看出在复频域进行NMF语音增强具有明显优势，有效提高了语音增强的性能。对比文献[7]、KL-CNMF语音增强算法评估值可知，在同一背景噪声环境下进行比较，随着信噪比的增加，KL-CNMF语音增强算法具有更高的评估值，PESQ与STOI值约提升0.08～0.3，SDR值约提升0.5～2，SSNR值约提升0.2～0.5，说明采用该算法进行语音增强能够在一定程度上削弱噪声的影响，减少相位信息的损失，提高语音质量。原因在于文献[7]算法采用了欧氏距离作为目标函数，其异常点误差易被放大，而采用KL散度函数度量误差可以有效克服了这一缺点。

(a) PESQ评分增量

(b) STOI评分增量

(c) SDR评分增量

(d) SSNR评分增量

图4 Factory1背景噪声环境下不同语音增强算法的PESQ, STOI, SDR, SSNR平均值

Fig.4 Average values of PESQ, STOI, SDR and SSNR for different speech enhancement algorithms under Factory1 noise background

(a) PESQ评分增量

(b) STOI评分增量

(c) SDR评分增量

(d) SSNR评分增量

图5 Babble背景噪声环境下不同语音增强算法的PESQ, STOI, SDR, SSNR平均值

Fig.5 Average values of PESQ, STOI, SDR and SSNR for different speech enhancement algorithms under Babble Babble noise background

结合表2与图4～6可以看出，对相位谱进行调制后的KL-CNMF算法(文献[11]算法与本文算法)能够较好地提高该算法性能，但是，在同一背景噪声环境、不同信噪比条件下，采用文献[11]算法进行相位谱调制，在较好地提高了PESQ值约0.02～0.15、SSNR值约2~3的同时，明显降低了STOI值约0.03～0.06、SDR值约1~2。这说明采用文献[11]算法虽然能够较好地提高语音质量和可懂度，但重构语音清晰度不仅没有提高，且造成语音失真，尤其是在低信噪比条件下这种影响最为突出。而本文算法提高了SDR值约1～2.5、STOI值约0.05～0.1，且相比文献[11]算法，PESQ值约提升0.1～0.2，SSNR值约提升0.5～1.5，这说明本文提出的改进的PSC算法采用STFT一致性约束较好地弥补了由文献[11]算法固定参数与反对称函数的应用而造成的失真现象，并结合KL-CNMF算法构成的语音增强模型能够在不牺牲语音可懂度的条件下，较好地提高了重构语音的质量与可懂度。

(a) PESQ评分增量

(b) STOI评分增量

(c) SDR评分增量

(d) SSNR评分增量

图6 Hfchannel背景噪声环境下不同语音增强算法的PESQ, STOI, SDR, SSNR平均值

Fig.6 Average values of PESQ, STOI, SDR and SSNR for different speech enhancement algorithms under Hfchannel noise background

4.3 语谱图分析

图7给出了不同的CNMF算法的语谱图，其中输入信噪比为0 dB，背景噪声为Factory1噪声。由语谱图上颜色的深浅和其对应的评估值大小来反映语音增强效果，颜色越深说明语音频谱的能量越强。由图7可知，KL-CNMF算法语谱图相比文献[7]算法中帧间的残余噪声相对较少且语谱更加清晰，说明采用KL散度模型度量误差的CNMF算法可以达到语音增强的目的，且相比于传统算法具有更好的噪声抑制能力，但语音段仍存在较多残余噪声。

(a) 纯净语音

(b) 带噪语音(PESQ=1.56, SDR=0.39, STOI=0.77, SSNR=-2.98)

(c) 文献[7]算法(PESQ=2.01, SDR=6.09, STOI=0.76, SSNR=0.31)

(d) KL-CNMF算法(PESQ=2.32, SDR=7.91, STOI=0.89, SSNR=0.64)

(e) 文献[11]算法(PESQ=2.51, SDR=6.45, STOI=0.87, SSNR=2.47)

(f) 本文算法(PESQ=2.66, SDR=9.24, STOI=0.91, SSNR=2.98)

图7 输入信噪比为0 dB的Factory1背景噪声环境下各算法语谱图

Fig.7 Spectrograms for different speech enhancement algorithms underFactory 1 noise background with input SNR of 0 dB

结合图7中矩形框可以看出，图7(e)与图7(f)语音段的残余噪声相对较少，这是由于其对重构语音的相位谱进行了补偿，而非直接采用带噪语音相位谱重构语音，但图7(e)颜色明显较浅且其SDR和STOI评估值偏低，这说明文献[11]算法以牺牲语音清晰度为代价，提高重建语音质量。而图7(f)颜色较深且各评估值均有提高，这说明本文采用的语音增强算法不仅在复频域中有效地利用了相位信息重构增强信号的幅度谱，且采用STFT一致性约束有效的克服了文献[11]算法造成的语音失真现象，进一步修正语音信号的相位谱。因此，该算法能够有效地减少失真，提高噪声抑制的能力，较好地保证重构语音质量，实现语音增强。

5 结论

对于单通道非负矩阵分解语音增强算法忽略相位信息的问题，本文提出了改进的KL复非负矩阵分解语音增强算法。该算法在复频域中构建了KL散度下的目标函数度量误差，克服了传统CNMF算法的缺点，并结合改进的相位谱调制算法，进一步减少了相位信息的丢失，保证了重构语音的质量，实现了语音增强。实验结果表明，在不同的环境噪声和信噪比条件下，本文算法相比文献[7]算法更好地抑制了背景噪声，提高了重构增强语音的清晰度，并克服了文献[11]算法SDR较低的缺点，进一步提高语音质量与可懂度，减少了语音失真。

目前单通道语音增强算法较少利用相位信息进行增强语音，修正的相位谱对语音质量和可懂度有较大提升，所以针对语音信号相位谱的修正算法还需进一步研究。

[1] 蔡宇, 郝程鹏, 侯朝焕. 采用子带谱减法的语音增强[J]. 计算机应用, 2014, 34(2): 567-571.

CAI Yu, HAO Chengpeng, HOU Chaohuan. Speech enhancement using subband spectral subtraction[J]. Computer applications, 2014, 34(2): 567-571.

[2] BORGSTROM B J, ALWAN A. Log-spectral amplitude estimation with generalized Gamma distributions for speech enhancement[C]//IEEE International Conference on Acoustics, Speech and Signal Processing, IEEE, 2011: 4756-4759.

[3] JABLOUN F, CHAMPAGNE B. Incorporating the human hearing properties in the signal subspace approach for speech enhancement[J]. Speech & Audio Processing IEEE Transactions on, 2010, 11(6): 700-708.

[4] LEE D D, SEUNG H S. Algorithms for non-negative matrix factorization[C]//International Conference on Neural Information Processing Systems, MIT Press, 2000: 535-541.

[5] CHUNG H, PLOURDE E, CHAMPAGNE B. Basis compensation in non-negative matrix factorization model for speech enhancement[C]//IEEE International Conference on Acoustics, Speech and Signal Processing. IEEE, 2016: 2249-2253.

[6] MAGRON P, BADEAU R, DAVID B. Complex NMF under phase constraints based on signal modeling: Application to audio source separation[C]//2016 IEEE International Conference on Acoustics, Speech and Signal Processing(ICASSP), Shanghai, 2016: 46-50.

[7] KAMEOKA H. Complex NMF: A new sparse representation for acoustic signals[C]//IEEE International Conference on Acoustics, Speech and Signal Processing, IEEE Computer Society, 2009: 3437-3440.

[8] HE W, ZHANG H Y, ZHANG L P. Sparsity-regularized robust non-negative matrix factorization for hyperspectral unmixing[J]. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2016, 9(9): 4267-4279.

[9] FEVOTTE C, IDIER J. Algorithms for nonnegative matrix factorization with the-divergence[J]. Neural Computation, 2011, 23(9): 2421-2456

[10] STARK A P, WOJCICKI K, LYONS J, et al. Noise driven short time phase spectrum compensation procedure for speech enhancement[C]//Proceedings INTERSPEECH, Australia, 2008: 549-552.

[11] LI Z, WU W, ZHANG Q, et al. Speech enhancement using magnitude and phase spectrum compensation[C]//Ieee/acis, International Conference on Computer and Information Science. IEEE, 2016: 1-4.

[12] ROUX J L, KAMEOKA H, ONO N, et al. Phase initialization schemes for faster spectrogram consistency based signal reconstruction[C]//Acoustical Society of Japan Autumn Meeting, No. 2010, 601-602.

[13] ROUX J L, VINCENT E, MIZUNO Y, et al. Consistent wiener filtering generalized time-frequency masking respecting spectrogram consistency[C]//International Conference on Latent Variable Analysis and Signal Separation, Springer-Verlag Berlin Heidelberg, 2010: 89-96.

WILSON K W, RAJ B, SMARAGDIS P, et al. Speech denoising using nonnegative matrix factorization with priors[C]//IEEE International Conference on Acoustics, Speech and Signal Processing, IEEE, 2008: 4029-403.

Speech enhancement based on improved Kullback-Leibler complex non-negative matrix factorization

XU Ming, WANG Dong-xia, ZHOU Cheng-xu, ZHANG Wei

(College of Electronic and Information Engineering, Liaoning University of Technology, Jinzhou 121001, Liaoning, China)

Considering the problem that the single channel non-negative factorization speech enhancement algorithm neglects phase information, a speech enhancement algorithm based on improved Kullback-Leibler complex non-negative matrix factorization is proposed in this paper. This algorithm takes into account the influence of the objective function when the traditional non-negative matrix factorization (NMF) algorithm is used to enhance the speech in the complex frequency domain, an objective function under Kullback-Leibler divergence in the complex frequency domain is constructed, and the phase spectrum of the reconstructed speech data is further corrected by the phase spectrum compensation algorithm (PSC) with spectral consistency constraints. Experimental results show that the proposed algorithm has obvious speech enhancement effect under different non-stationary environments especially in low signal-to-noise ratio (below 0 dB), and the increment of performance evaluation index is higher; moreover, it can overcome the disadvantage of low source distortion rate caused by the traditional phase spectrum compensation algorithms, further reduce speech distortion and restrain background noise to realize speech enhancement.

complex nonnegative matrix factorization; phase spectrum compensation; speech enhancement

TN912.35

A

1000-3630(2019)-05-0560-08

10.16300/j.cnki.1000-3630.2019.05.013

2018-06-12;

2018-08-18

辽宁省科学事业公益研究基金项目(20170056)、辽宁省自然科学基金资助(201302022)项目。

许铭(1994－), 男, 辽宁沈阳人, 硕士研究生, 研究方向为现代信号处理与多媒体技术。

王冬霞,E-mail: dxwang_lg@126.com